Założenia ośrodka ciągłości: jego właściwości nie zmieniają się przy przechodzeniu do objętości nieskończenie małych.
Założenie ciągłości odkształceń: dwie cząsteczki, które się stykały w miarę deformacji, obciążeń nadal się stykają, jedynie mogą się zdeformować.
Metoda Lagrange'a jest analizą wędrowną, polega na badaniu właściwości fizycznych( np.: prędkość, gęstość, ciśnienie, temperatura) i opisie poruszającego się płynu. W tej metodzie należy wybrać cząstkę np. poprzez opisanie jej położenia w czasie t0 otrzymujemy wtedy: x0, y0, z0 a następnie śledzi się dana cząstkę w kolejnych chwilach t. Otrzymujemy w ten sposób opis ruchu płynu w postaci funkcji współrzędnych położenia początkowego i czasu:![]()
= f (x0, y0, z0, t) gdzie ![]()
jest współrzędną położenia lub własnością płynu w chwili t.. Współrzędne położenia elementu płynu w kolejnych chwilach czasowych, wyrażające parametryczne równanie toru cząsteczki określają równania:
x =x(x0,y0, z0, t); y= y(x0, y0, z0, t); z = z(x0,y0,z0, t)
Składowe prędkości poszczególnych elementów płynu wynoszą:
Vx = ∂x/∂t; Vy = ∂y/∂t; Vz = ∂z/∂t
a składowe przyspieszenia:
ax = ∂2x/∂t2; ay = ∂2y/∂t2; az = ∂2z/∂t2
Inne parametry stanu ruchu płynu np. gęstość i ciśnienia, wyraża się zgodnie ze wzorem:
![]()
= f (x0, y0, z0, t) a więc:
ρ = ρ (x0, y0, z0, t); p = p (x0, y0, z0, t)

Metoda Eulera - analiza lokalna
Opisuje zmiany wielkości fizycznej płynu z poszczególnych punktów przestrzeni, w której odbywa się ruch. Vx = f (R, t)
Vx = fx(x, y, z, , t) Vy = fy(x, y, z, , t)
Vz = fz(x, y, z, , t)
![]()
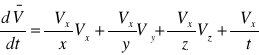
-przyśpieszenie cząsteczki wyrażone za pomocą pochodnej substancjalnej
Zależność między L i E:
![]()
Linia prądu - linia pola wektorowego definiowana dla pewniej chwili. W każdym miejscu jest styczna do wektora prędkości w tym miejscu.
Tor cząstki - linia zakreślona przez cząsteczkę płynu w ruchu.
Linia prądu = tor cząstki dla ruchu ustalonego dla zmiennego w czasie jest inaczej.
Smuga - miejsce geom. Zajmowane przez cząstki, które przeszły przez określony punkt w przestrzeni.
Wzory ściśliwości i rozszerzalności.
Ściśliwość - to zdolność do zmiany gęstości płynu w danej temperaturze przy zmianie ciśnienia. Uwzględnia zmianę gęstości płynu przypadającą na jednostkę przyrostu ciśnienia dla stałej temperatury ośrodka: β = (1/ρ)(dρ/dp)
Rozszerzalność - zdolność do zmiany gęstości płynu przy stałym ciśnieniu, temperaturze pod wpływem zmiany temperatury. Wyraża względną zmianę gęstości przypadającą na jednostkę przyrostu temperatury przy danym ciśnieniu:
α = - (1/ρ)(dρ/dT)
Równanie stanu:
dρ /ρ = (1/ρ)(dρ/dp) dp + (1/ρ)(dρ/dT) dt =
βdp - αdT
zmiana funkcji (gęstości) pod wpływem ciśnienia i temperatury
Wzory Helmholtza:
Vx= Vxo +∂Vx/∂x ξ +∂Vx/∂y η+ ∂Vx/∂z ζ
Vy= Vyo +∂Vy/∂x ξ +∂Vy/∂y η+ ∂Vy/∂z ζ
Vz= Vzo +∂Vz/∂x ξ +∂Vz/∂y η+ ∂Vz/∂z ζ
przemieszczenie obrót zmiana czasu
∂Vx/∂z ζ+ ∂Vy/∂z ζ- deformacja
∂Vx/∂z ζ- ∂Vy/∂z ζ- obrót
Co to znaczy ∂Vx/∂x, ∂Vy/∂y , ∂Vz/∂z
założenia: Vz= 0, ∂ /∂z =0, ∂Vy/∂x= 0, ∂Vx/∂y =0
∂Vx/∂x - zmiana prędkości w kierunku ruchu, droga jaką przebyła cząsteczka względem P(0,0)
AA'=∂Vx/∂x* ξ*dt +∂, BB'=∂Vy/∂y*η*dt. Cząsteczka nie przemieściła się, lecz zmieniła swoje wymiary, nie zmieniła kształtu
Prędkość wydłużenia względnego
εx = ∂Vx/∂x, εy = ∂Vy/∂y, εz = ∂Vz/∂z
Szybkość wydłużenie względnego = wydłużenie względne/czas
Wydłużenie względne = wydłużenie/ wartość początkowa
Względna prędkość objętości:
∂Vx/∂x ξ+∂Vy/∂y η+∂Vz/∂z ζ
Względna szybkość zmiany przyrostu objętości:
∂Vx/∂x +∂Vy/∂y +∂Vz/∂z =div V(wektor) = F
Jeżeli div V jest ujemne to cząstka zmniejsza swoją objętość
Co to znaczy ∂Vx/∂y, ∂Vy/∂x
założenia: Vz=0, ∂ /∂z= 0 , ∂Vx/∂x=0, ∂Vy/∂y=0
AA'=∂Vy/∂x *ξ*dt , BB'=∂Vx/∂y*η*dt. Przekątna cząstki zmieniła krawędź, cząstka uległa obróceniu.
dβ=(dα1- dα2)/2=dt(∂Vy/∂x+ ∂Vx/∂y)/2
Prędkość kątowa obrotu cząstki dookoła osi z
ωz=(∂Vy/∂x - ∂Vx/∂y)/2= Ωz*1/2= 1/2*(rot V wektor)z
(rot V wektor)z - wektor rotacji
Ωz - szybkość z jaka przesuwają się boki po przekątnych
Szybkość, z jaka przesuwają się boki do osi cząsteczki
θ z= (dα1+ dα2)/ (2dt) - szybkość kątowa dwóch ścianek względem siebie
1/2θ z= (∂Vy/∂x+ ∂Vx/∂y)/2
θ z+Ωz=∂Vy/∂x-∂Vx/∂y+∂Vy/∂x+∂Vx/∂y
∂Vy/∂x=1/2(θ z+Ωz) deformacja kątowa
∂Vx/∂y= 1/2(θ z-Ωz) szybkość obrotu
Równanie Eulera:
![]()
Założenia: płyn jest nie lepki ν = 0
dv/dt - siły bezwładności
Fmj - siły masowe jednostkowe
1/ρ grad p - siły powierzchniowe normalne
Ruch turbulentny - duża wartość Re, energia przekazywana z ruchu podstawowego do pulsacyjnego jest większa niż ciepło wytworzone na skutek tarcia. W efekcie przepływ traci stateczność, zaburzenia wzmagają się i rozprzestrzeniają się.
Wartość przeciętna prędkości:
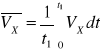
Wartość przeciętna:
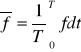
Dla ustalonych warunków brzegowych pole parametrów jest stałe.
Pulsacja:
![]()
z def: 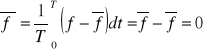
Przeciętna wartość pulsacji jest równa zero.
Intensywność turbulencji:
![]()
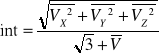
Drgania niewielkie, ale bardzo szybkie.
Turbulencja izotropowa:
![]()
Niezależna od kierunku.
Równanie ruchu Reynoldsa
Jest to równanie Reynoldsa dla składowej x, dotyczącego przepływów turbulentnych.
Dla ruchu turbulentnego oprócz tarcia wynikającego z lepkości pojawia się tarcie turbulentne:
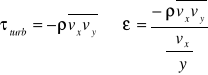
gdzie(-ρ) odpowiada za turbulentne naprężenia styczne.
Ε - współczynnik lepkości burzliwej turbulentnej
Naprężenie to działa na powierzchni xy, więc jest prostopadłe do osi z.
Założenia teorii Prandtla.
Przepływ płynu charakteryzuje się dużymi wartościami liczby Re, siły lepkości nie odgrywają istotnych zmian i można je pominąć. Ze wzrostem Re przepływ przybiera charakter płynu nielepkiego.
Założenia:
- ruch płaski, nie ma prędkości w trzecim kierunku oraz zmian prędkości
- prędkości w kierunku x są dużo większe od prędkości w kierunku y.
- zmiany czegokolwiek w kierunku y są o wiele większe niż w kierunku x.
Teoria ta określa związek między naprężeniami τ turbulentnymi a prędkością uśrednioną.
W strefie laminarnej - τL > τT
W strefie przejściowej - τL = τT
W strefie turbulentnej - τL < τT
![]()
gdzie Vx i Vy to uśrednione prędkości w kierunku odpowiednich osi
Teoria Prandtla mówi o związku pomiędzy naprężeniami turbulentnymi a prędkością uśrednioną
Wzór na przeciętną wartość prędkości:
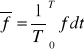
dla teorii Prandtla
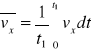
Naprężenia styczne turbulentne
![]()
w teorii Prandtla
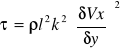
Prawo zachowania masy:
![]()
1 - zmiana masy w obszarze uwarunkowana zmianą gęstości płynu
2 - ilość masy doprowadzana lub odprowadzana z ośrodka
W objętości kontrolnej, zmiana masy w ośrodku równa jest masie doprowadzanej lub odprowadzanej z obszaru.
Prawo zachowania pędu:
![]()
1-zmiana pędu
2-impuls sił masowych
3-impuls sił powierzchniowych
Suma wszystkich sił plus siła bezwładności jest równa zeru.
Prawo zachowania energii bilansowe równanie
Energia kinetyczna zmienia się w wyniku pracy wykonanej przez siły masowe i powierzchniowe
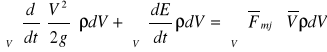
![]()
1-wszy człon - zmiana energii kinetycznej w czasie
2-gi człon -ilość ciepła w objętości, zmiana energii wewnętrznej na jednostkę masy
![]()
strumień ciepła, ciepło
![]()
-praca sił skalarnych = wykonana praca
Równanie zachowania energii mechanicznej
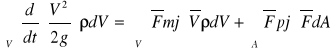
Energia kinetyczna zmienia się w pracy wykonanej przez siły masowe i powierzchniowe
Równanie zachowania(bilansowe) ciepła
![]()
RÓWNANIE NAVIERA-STOKESA
Równanie analizy ruchu płynu lepkiego w postaci wektorowej:
dV /dt = Fmj - 1/ρ gradp + ν ∇2V + ν/3*grad* divV
1 - siła bezwładności;
2 - działanie sił masowych;
3 - różnica sił normalnych, działanie sił powierzchniowych normalnych
4 - siła tarcia stycznego, szybkość poślizgu;
2,3,4 - efekt sił tarcia;
5- dodatkowe siły tarcia związane ze zmianą objętości cząstki, siły tarcia styczne związane ze zniekształcaniem się płynu ściśliwego
Równanie opisuje przepływ płynów przy Założeniach: płyn ma własność lepkości (płyn Newtowski), pola prędkość są ciągle i różniczkowalne
Przypadki szczególne (modyfikacje N-S)
(krzyżyk przed oznacza wektor):
1)płyn nieściśliwy (*=const => div#υ = 0)
d#υ/dt = #Fmj-1/ρ gradp+mi∇2#V
2)płyn nie lepki (mi=0)
d#υ/dt = #Fmj-1/ρ gradp - równanie Eulera
3)płyn nieruchomy albo w ruchu jednostajnym
(brak ruchu względnego) dv/dt = 0
0 = #Fmj-1/ρ gradp - równanie statyki
Modyfikacja
d#υ/dt = #Fmj-1/ρ gradp N-S mówi o tym ze gdy płyn jest nielekki to stosowane jest równanie zmodyfikowane
Założenia: 1) mi=0 , 2) ruch ustalony , 3) płyn barotropowy ro=f(p) , Fmj = grad - siły masowe powodują potencjał
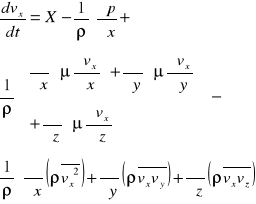
Wyszukiwarka