Wydział: FTiMK	Imię i Nazwisko: Marcin Wiśniowski	Nr. Zespołu 5	Ocena Ostateczna
Grupa: Druga	Tytuł ćwiczenia: Badanie rezonansu elektrycznego w układzie RLC	Nr. Ćwiczenia 18	Data Wykonania: 18.10.2002

1. Wprowadzenie

W obwodzie elektrycznym złożonym z opornika o oporze R, kondensatora o pojemności C i cewki indukcyjnej o indukcyjności L, do którego przyłożymy napięcie harmonicznie zmienne:

U = U_osinωt

Prąd przemienny:

I = I_osin(ωt + ϕ)

W języku potocznym przyjęło się nazywać prąd przemienny, któ­rego natężenie i napięcie zmieniają się sinusoidalnie w czasie, prądem zmiennym. W praktyce wygodnie jest posługiwać się natężeniem i napięciem skutecznym prądu zmiennego.

Natężeniem skutecznym prądu przemiennego I_sk nazywamy takie natężenie prądu stałego, który wydziela w tym samym czasie, tę samą ilość energii co da­ny prąd przemienny.

Posługując się napięciem i natężeniem skutecznym, możemy dla prądu zmiennego stosować te same prawa, co dla prądu stałego, tj. prawa: Ohma i Kirchhoffa. Opór Z obwodu prądu przemiennego nosi nazwę impedancji i definiujemy go:

Prąd zmienny płynąc przez opór omowy R wywołuje spadek potencjału:

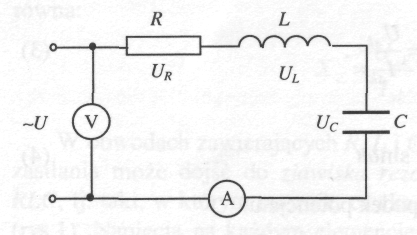
U_R = IR = I_oRsinωt

nie ma zatem przesunięcia fazowego między prądem i napięciem impedancja jest równa R.

Natomiast napięci U_L na cewce, gdy płynie przez nią prąd przemienny.

Widzimy, że napięcie na cewce wy­przedza prąd w fazie o π/2

Podobnie prąd zmienny płynąc przez kondensator o pojemności C wy­wołuje spadek potencjału U_c na jego okładkach równy:

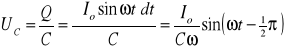
W tym wypadku napięcie opóźnia się w fazie względem prądu o π/2 (prąd wyprzedza napięcie o π/2).

W obwodach zawierających R, L i C dla pewnych częstości zmian napięcia zasilania może dojść do zjawiska rezonansu. Rozważmy szeregowy obwód RLC, tj. taki, w którym opornik, cewka i kondensator połączone są szeregowo. Sumując wektory napięcia na każdym z elementów otrzymujemy:

a impedancja dana jest wzorem

Kąt przesunięcia fazowego prądu względem napięcia obliczamy ze wzoru:

Przykładając do szeregowego obwodu RLC zmienne napięcie (1), otrzymujemy prąd o natężeniu skutecznym:

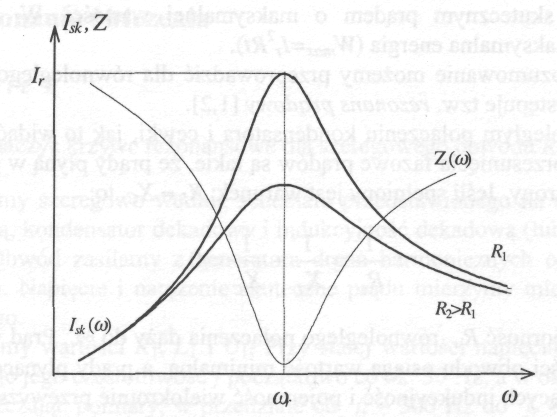
Rezonans polega na maksymalnym przekazywaniu energii z jednego układu drgającego do drugiego. Zachodzi to wówczas, gdy częstotliwości drgań tych układów są równe. Zjawisko rezonansu występuje również w obwodach RLC. Z powyższego równania wynika, że dla danych elementów R, L i C największy prąd popłynie wówczas, gdy:

co odpowiada warunkowi: X_L = Xc Uwzględniając przesunięcie fazowe otrzy­mujemy łączny spadek potencjału na cewce i kondensatorze równy 0. W ob­wodzie szeregowym RLC występuje wówczas tzw. rezonans napięć dla często­tliwości rezonansowej ω_r bliskiej częstotliwości drgań własnych układu

a prąd rezonansowy I_r przyjmuje wartość daną wyrażeniem:

W obwodzie wydziela się maksymalna energia W_max = I_r²Rt

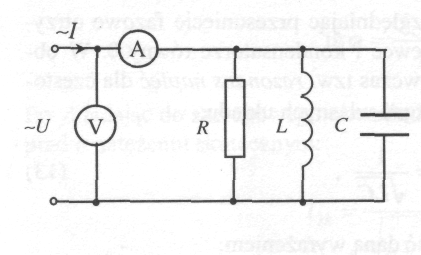
Podobne rozumowanie możemy przeprowadzić dla równoległego obwodu RLC, gdzie występuje tzw. rezonans prądowy. Przy równoległym połączeniu kondensatora i cewki, przesunięcia fazowe prądów są takie, że prądy płyną w gałęziach w przeciwne strony. Jeśli spełniony jest warunek: X_L=Xc, to:

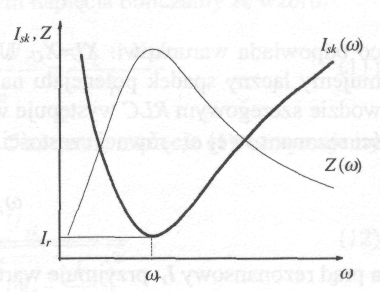
wypadkowa oporność R_w równoległego połączenia dąży do ∞. Prąd w nie rozgałęzionej części obwodu osiąga wartość minimalną, a prądy płynące w gałę­ziach zawierających indukcyjność i pojemność wielokrotnie przewyższają prąd źródła - mówimy o rezonansie prądowym. Impedancja dana jest wzorem:

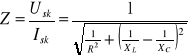
2. Tabele Pomiarowe

R1= 50 Ω L1= 150 mH C1= 1,1 μF Usk= 2 V			R2= 70 Ω L2= 200 mH C2=1,1 μF Usk= 2 V			R3= 2 kΩ L3= 50 mH C3= 1,2 μF Usk= 2 V			R1=........ L1=........ C1=........ Usk=........
f Hz	Isk mA	Z Ω	f Hz	Isk mA	Z Ω	f Hz	Isk mA	Z Ω	f Hz	Isk mA	Z Ω
50	0,7	2857,1	50	0,69	2898,5	100	37,8	52,9
100	1,46	1369,8	100	1,50	1333,3	200	24,5	81,6
150	2,39	836,8	150	2,53	790,5	300	15,9	125,7
200	3,62	552,5	200	4,07	491,4	400	10,2	196,0
250	5,38	371,7	250	6,68	299,4	500	6,0	333,3
300	8,18	244,5	300	11,21	178,4	600	3,4	588,2
320	9,64	207,4	320	13,03	153,5	620	3,1	645,1
340	11,23	178,1	340	13,63	146,7	640	2,9	689,6
360	12,72	157,2	360	12,76	156,7	660	2,8	714,3
380	13,61	146,9	380	11,23	178,1	680	2,9	689,6
400	13,64	146,6	400	9,72	205,8	700	3,1	645,2
420	12,88	155,2	450	6,96	287,4	800	4,5	444,4
440	11,77	169,9	500	5,37	372,4	900	6,7	298,5
460	10,59	188,8	550	4,39	455,6	1000	8,7	229,9
480	9,49	210,7	600	3,73	536,2	1100	10,8	185,2
500	8,55	233,9	650	3,23	619,2	1200	12,7	157,5
550	6,78	294,9	700	2,88	694,4	1300	14,6	137,0
600	5,62	355,9				1400	16,3	122,7
650	4,79	417,5				1500	18,2	109,9
700	4,19	477,3				1500	19,9	100,5
800	3,38	591,7				1700	21,7	92,2
900	2,84	704,2				1800	23,2	86,2

3. Obliczenia

Impedancje dla każdego układu liczę ze wzoru




Częstotliwość rezonansową dla każdej krzywej I_sk(f) wyznaczam ze wzoru:




• Dla pierwszego pomiaru







• Dla drugiego pomiaru







• Dla trzeciego pomiaru







4. Wnioski

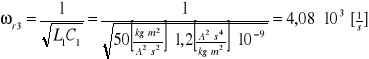
Przeprowadzone ćwiczenie miało na celu zbadanie częstotliwości rezonansowej dla obwodów RLC oraz przeanalizowanie wpływu zmian elementów RLC na krzywe rezonansowe.

Zaczynając wyniki z pomiarów są bardzo zbliżone do częstotliwości zliczonej:

Wartość zliczona	Wartość wyznaczona
391,7 Hz	390 Hz
339,5 Hz	340 Hz
650 Hz	660 Hz

Zmianą indukcyjności cewki bądź pojemności kondensatora można sterować częstotliwością rezonansową, wraz ze wzrostem tych wartości częstotliwość rezonansowa maleje.

Zmieniając opór układu jesteśmy wstanie regulować impedancje układu.

Dla połączenia szeregowego wraz z jego wzrostem maleje zakres częstotliwości w których płynie prąd.

Niestety z powodu przeprowadzenia tylko jednego doświadczenia dla obwodu równoległego pozwala mi tylko zgadywać wpływ zmian elementów RLC na krzywe rezonansowe

3

---