prof. Teresa K. Ryzyko w działalności gospodarczej WSB
Program wykładu
Idea kontrolowania ryzyka (historyczne podłoże
koncepcji ryzyka, podstawowe pytania, jakie stawia sobie
teoria ryzyka)Niepewność i ryzyko jako kategorie ekonomiczne
(ontologia ryzyka)Indywidualne postawy wobec ryzyka
Metody pomiaru ryzyka i niepewności
Rodzaje ryzyka i sposoby jego neutralizacji
(ubezpieczenie jako czynnik ograniczenia ryzyka)Najważniejsze aspekty aplikacyjne teorii ryzyka
ryzyko w działalności banków komercyjnych wybór portfela inwestycyjnego
Literatura:
1. P.L. Bernstein: Przeciw bogom. Niezwykłe dzieje ryzyka, Warszawa 1997
2. 3.
4.
E. Ostrowska: Ryzyko inwestycyjne, Gdańsk 1999
M. Wierzbińska: Ryzyko w gospodarce rynkowej, Lublin 1996
Ryzyko w działalności banków komercyjnych, praca zbiorowa, Poznań 2000
W. F. Samuelson, S.G. Marks: Ekonomia menedżerska,
Warszawa 1998K. Marcinek: Ryzyko projektów inwestycyjnych, AE
Katowice 2000
Cele wykładu:
jak ryzyko i niepewność wpływają na podejmowanie decyzji
przez jednostki, nie tylko gospodarcze,
jak można zmierzyć ryzyko i jakie instytucje ekonomiczne,
umożliwiają dokonywanie wyboru w warunkach ryzyka.
1. Idea kontrolowania ryzyka
Chociaż wykład dotyczy działalności ekonomicznej, to ryzyko i niepewność jest wszechobecną cechą codziennego życia, ponieważ występuje w wielu naukach i wszystkich płaszczyznach działalności ludzkiej. Państwo zaskakuje obywateli nowymi podatkami (np. katastralny), przedsiębiorstwo - redukcją zatrudnienia, chirurg nie zaprzecza wystąpienia ryzyka pooperacyjnego, student - ryzyka niezaliczenia przedmiotu, użytkownik urządzenia mechanicznego możliwości jego awarii, itp. Jak powiedział J.M. Keynes: „Są tylko dwie rzeczy pewne na świecie: to, że umrzemy i to, że musimy płacić podatki".
Istota kontrolowania ryzyka polega na maksymalizowaniu zakresu zagadnień, w odniesieniu do których jesteśmy w stanie, choćby w pewnym stopniu, przewidzieć skutki zdarzeń, oraz minimalizowaniu tych obszarów, gdzie związki przyczynowo-skutkowe pozostają całko wicie poza naszą kontrolą i są nieznane.
Tło historyczne prezentowanej koncepcji ryzyka
Tysiące lat temu znano mapę nieba, zbudowano bibliotekę aleksandryjską, prowadzono wykłady z geometrii euklidesowej, pisano arcydzieła literackie, lecz rewolucyjną ideą, która wyznacza cezurę między nowożytnością a wcześniejszymi epokami historycznymi jest idea kontrolowania ryzyka, tj. pogląd, że przyszłość nie jest jedynie kaprysem bogów, a ludzie nie są bezradni wobec sił przyrody. Dopóty ludzie nie potrafili radzić sobie z niepewnością przyszłość była tylko zwierciadłem przeszłości lub mroczną domeną kapłanów, wyroczni i wróżbitów, którzy zazdrośnie strzegli swego monopolu na wiedzę o przewidywanym biegu wypadków.
Umiejętność formułowania precyzyjnych prognoz dotyczących możliwego przebiegu przyszłych zdarzeń i dokonywania wyborów między rozmaitymi alternatywami jest najistotniejszym aspektem życia współczesnych społeczeństw. Kontrolowanie ryzyka wyznacza kierunek ludzkich działań w tak różnorodnych dziedzinach wiążących się z podejmowaniem decyzji, jak alokacja zasobów pieniężnych, tworzenie systemu powszechnej opieki zdrowotnej, prowadzenie wojny, planowanie rodziny, wpłacanie składek ubezpieczeniowych, montowanie pasów bezpieczeństwa w samochodach i samolotach, prowadzenie działalności rolniczej, inwestycyjnej, produkcyjnej lub marketingowej.
Cały czas trzeba sobie zdawać sprawę z prawdopodobieństwa wystąpienia awarii i błędów. Bez tego nie można byłoby podejmować żadnego działania w żadnej dziedzinie. Nie byłoby postępu ani w technice, ani w gospodarce, ani w medycynie, ani w życiu społecznym. Gdyby nie istniały różne formy ubezpieczeń, niespodziewane przykre zdarzenia losowe powodowałyby rozprzestrzenianie się ubóstwa. Bez rynków finansowych oszczędności narażone byłyby na znaczne wahania ich siły nabywczej wskutek najdrobniejszych zakłóceń gospodarczych (niemożliwe byłoby rozproszenie ryzyka).
Umiejętność kontrolowania ryzyka wespół ze skłonnością do ryzykownych przedsięwzięć i podejmowania dalekowzrocznych decyzji są podstawowymi składowymi siły, która jest motorem rozwoju ludzkości.
,( Nowoczesna koncepcja ryzyka ma swoje źródło w indoarabskim systemie liczbowym, który rozpowszechnił się w świecie zachodnim przed siedmioma lub ośmioma wiekami, a poważne badania rozpoczęły się w dobie renesansu, kiedy ludzie zakwestionowali dotychczasowe poglądy^W 1654 r. francuski szlachcic de Merę (z zamiłowania matematyk i hazardzista) rzucił wyzwanie słynnemu matematykowi Pascalowi zadając mu następującą zagadkę. Chodziło o podzielenie puli w pewnej niedokończonej grze losowej, kiedy jeden z graczy wyprzedza rywala o jedno posunięcie. Owa zagadka wprawiała w zakłopotanie matematyków od dłuższego czasu, kiedy po raz pierwszy sformułował ją mnich L. Paccioli,
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
zwracając uwagę ówczesnym działaczom gospodarczym na możliwość podwójnego księgowania. Owocem współpracy Pascala i pewnego prawnika i jednocześnie matematyka był intelektualny dynamit. Prosta gra, która może uchodzić za siedemnastowieczną wersję chińczyka doprowadziła do odkrycia teorii prawdopodobieństwa, matematycznego rdzenia teorii ryzyka. Warto zwrócić uwagę, że była to epoka powszechnych odkryć geograficznych oraz fali innowacji i nowatorskich wynalazków (proch strzelniczy, ruchoma czcionka, umiejętność posługiwania się perspektywą przez artystów, układ krwionośny, odwrót od mistycyzmu w wynika wystąpienia Marcina Lutra).
To, że obecnie nie opieramy się już na przesądach i tradycji w takim stopniu, jak to czynili nasi przodkowie, nie wynika stąd, że jesteśmy bardziej racjonalni, lecz stąd, że rozumienie natury ryzyka pozwala nam podejmować decyzje na podstawie racjonalnych przesłanek.
W miarę upływu czasu zabiegi matematyków sprawiły, ze teoria prawdopodobieństwa przestała być ciekawostką przyciągającą zainteresowanie hazardzistów, przeobrażając się w potężne narzędzie służące do porządkowania, interpretacji i praktycznego stosowania informacji-^od 1725 r. matematycy układali tabele przeciętnej długości życia, a w Londynie pojawiły się ubezpieczenia morskie jako nowa, doskonale prosperująca i wyrafinowana forma działalności gospodarczej). Jacob Bernulli w 1703 r. odkrywa prawo wielkich liczb (różnica między zaobserwowaną wartością z próby a wartością rzeczywistą będzie w miarę zwiększania liczby obserwacji w próbie) oraz metodę pobierania prób statystycznych, które legły u podstaw takich obszarów działalności jak badanie opinii publicznej, testowanie nowych leków, dobór portfela akcji. Leibnitz odpowiedział, że prawo to dotyczy większości przypadków, tym samym zastrzeżenie to daje klucz do zrozumienia przyczyn, dla których istnieje coś takiego jak ryzyko. Gdybywszystkie zdarzenia były przewidywalne, a w świecie, w którym każde zdarzenie jest identyczne z jakimś wcześniejszym zdarzeniem, nie zachodziłyby żadne zmiany^W 1730 r. Abraham de Moivre wprowadził koncepcję rozkładu normalnego i pojęcie odchylenia standardowego, dało to podstawę do sformułowania prawa średnich. Są one obecnie składnikami nowoczesnych technik ilościowego ujęcia ryzyka. Daniel Bernulli, siostrzeniec Jacoba, wyjaśnił - na podstawie koncepcji de Moivre'a o tym, że „zadowolenie wynikające z niewielkiego wzrostu zamożności będzie odwrotnie proporcjonalnie do ilości uprzednio posiadanych dóbr"- dlaczego król Midas był nieszczęśliwy, dlaczego ludzie wykazują tendencję do unikania ryzyka, i dlaczego ceny muszą spadać, jeżeli chcemy skłonić klientów, by kupowali więcej towarów. Twierdzenie D. Bernulliego stało się dominującym paradygmatem badań nad racjonalnością postępowania przez następnych dwieście pięćdziesiąt lat i położyło podwaliny pod nowoczesne zasady inwestowania. W pierwszej połowie osiemnastego wieku protestancki pastor Thomas Bayes posunął się naprzód badania w dziedzinie statystyki pokazując, w jaki sposób można podejmować decyzje na podstawie szerszego zasobu danych za pomocą matematycznej metody łączenia nowych i starych informacji. Twiedzenie Bayesa dotyczy tych powszednich sytuacji, kiedy rozporządza się trafną intuicyjną oceną prawdopodobieństwa jakiegoś zdarzenia i poszukuje się wiedzy, jak należy modyfikować tę ocenę w zależności od faktycznego przebiegu wydarzeń.
Niemal wszystkie narzędzia wykorzystywane obecnie w dziedzinie kontroli ryzyka, analizy procesów decyzyjnych i dokonywania wyborów, począwszy od ścisłej racjonalności teorii gier aż po śmiałe tezy teorii chaosu, mają swe źródło w odkryciach, których dokonano w latach 1654 - 1760. Dwa wyjątki:
1875 r. Francis Galton, matematyk - amator (bliski krewny Karola Darwina) odkrył regres]ę do średniej, która wyjaśnia, dlaczego „pycha poprzedza
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
upadek" i dlaczego chmury mają srebrzystą poświatę. Ilekroć podejmujemy decyzję opartą na oczekiwaniu, że rzeczy powrócą do „normalnego" stanu, odwołujemy się do pojęcia regresji do średniej;
w 1952 r. noblista Harry Markowitz wykazał za pomocą środków matematycznych, dlaczego umieszczenie wszystkich jajek w jednym koszyku jest strategią nadzwyczaj ryzykowną, a zaangażowanie środków w różne przedsięwzięcia jest najprostszym sposobem, który pozwala inwestorom i menedżerom uniknąć katastrofalnych następstw. Odkrycie to dało początek intelektualnemu trendowi, który zrewolucjonizował Wall Street, gospodarkę fmansowąi decyzje w sferze przedsiębiorczości i handlu na całym świecie.
Teoria ryzyka (od starowłoskiego risicare oznacza odważyć się) to osiągnięcia myśli ludzkiej w zakresie odpowiedzi na pytanie: jak racjonalnie zaprząc przyszłość w służbę teraźniejszości. Nie potrafimy ująć przyszłości w kategoriach ilościowych, gdyż pozostaje ona niewiadoma; nauczyliśmy się jednak posługiwać liczbami analizując zdarzenia, które wystąpiły w przeszłości.
W jakiej mierze można polegać na tym, co prawidłowości
zaobserwowane w przeszłości mówią nam o przyszłości?Co ma większe znaczenie w obliczu ryzyka: zaobserwowane fakty, czy
subiektywne przeświadczenia tego, co kryje się w otchłani czasu?Czy kontrolowanie ryzyka jest nauką, czy sztuką?
Czy nauka potrafi w ogóle definitywnie rozstrzygnąć, gdzie właściwie
przebiega granica między tymi dwoma sposobami ujmowania
rzeczywistości?
Innymi słowy, jak rozumieć ryzyko, jak je mierzyć i oceniać jego konsekwencje i jak przyczyniać się do rozwoju nowoczesnego społeczeństwa. Dzięki przemianie postaw wobec ujarzmiania ryzyka, ludzka namiętność uprawiania gier hazardowych i przyjmowania zakładów znalazła ujście w rozwoju gospodarczym, dążeniu do poprawy warunków życia i postępie technicznym. Skonstruowanie modelu matematycznego, który wydaje się wyjaśniać wszystkie zdarzenia, nie załatwia jeszcze wszystkiego. W obliczu zmagań z codziennością, kolejnych prób i błędów, niejednoznaczności faktów i siły ludzkich namiętności model łatwo traci na znaczeniu. Kości do gry, koło ruletki, bęben z liczbami totolotka, egzaminy wszelkiego rodzaju, rynek papierów wartościowych to naturalne laboratoria, które pozwalają uzyskać także wiedzę o ludzkiej naturze, kiedy rozstrzygnięcia w poszczególnych zdarzeniach wstrzymują oddech i przyspieszają pracę serca. Ryzyko jest swobodnym wyborem, a nie nieuchronnym przeznaczeniem.
2. Istota ryzyka
Czym jest ryzyko? Na to pytanie odpowiadano w setkach definicji. Na ogół twierdzi się, że ryzyko występuje wówczas, gdy podejmowane są działania o niepewnych i niepożądanych skutkach. Stąd też źródłem powstawania ryzyka w gospodarowaniu jest podejmowanie decyzji, dla których konieczne są właściwe przesłanki. Najważniejszą przesłanką jest wiedza o procesie, która pozwala na stawianie prognoz, zwłaszcza ekonometrycznych, charakteryzujących się małym, możliwym do przyjęcia prognozy błędem ex ante. Ogromne ryzyko pojawia się w sytuacji, gdy tylko tak zwany cud może sprawić pomyślny obrót wydarzeń, a ludzie pomimo to, decydują się na dane działanie. O ryzyku wiadomo już dużo. Najprecyzyjniej ryzyko definiuje się jako zmienną losową, czyli ryzyko a - jest prawdopodobieństwem wystąpienia wartości zmiennej x większej od pewnej ustalonej
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
apriorycznie wartości granicznej xq. Zatem a =f(x >xq). Trudność polega na tym, że funkcja /jest na ogół nieznana, więc należy posługiwać się jej szacunkiem/*. Tu pojawia się subiektywizm związany z wyborem metody estymacji i związanych z nią przyjmowanych założeń wstępnych, często nie poddających się empirycznej weryfikacji. Dlatego przyjęto do określania ryzyka parametr jego rozkładu, a mianowicie wariancję ó2, a dokładnie jej oszacowanie s2. Jest to nie tylko uproszczenie (parametr rozkładu zamiast całego rozkładu), lecz także subiektywizm związany z przyjętą metodą estymacji statystycznej parametrów rozkładu zmiennej. Dlatego dla precyzyjnego szacowania ryzyka poszukuje się takich rozkładów, które można zweryfikować empirycznie, przyjmując bardzo wysokie wymagania dotyczące precyzji oszacowań. Często proces ryzyka aproksymuje się za pomocą ruchu Browna lub jego modyfikacji, stosując już dość złożony aparat matematyczny.
Najczęściej w badaniach ekonomicznych występuje ryzyko związane z aktywami firmy. Wygodnie jest mierzyć ryzyko związane z danym aktywem do relacji do ryzyka rynku kapitałowego jako całości za pomocą tzw. współczynnika p. Współczynnik ten można zapisać jako:
P = (ryzyko akcji i); (ryzyko całego rynku kapitałowego).
Często współczynnik p przyjmuje się dla danego typu aktywów w sposób aprioryczny lub próbuje się go szacować.
Można jednak przyjąć, że ryzyko danego i-tego aktywu zależy od k zmiennych. Zatem ryzyko i-tego aktywu można zapisać jako funkcję wielu zmiennych g(xi, ...,x/J. Inaczej P jest ilorazxem dwóch wielowymiarowych (k-wymiarowych) rozkładów. Znając modele różnych rodzajów ryzyk można następnie wykorzystać je do dywersyfikacji ryzyka poprzez zmianę struktury aktywów w danej firmie. Prowadzi to bezpośrednio do dwóch zagadnień teoretycznych i praktycznych, tj. do poszukiwania punktów równowagi oraz do generowania zysków poprzez unikanie ryzyka. Konkludując, subiektywizm bierze się z przyjmowanych założeń apriorycznych o rozkładach i ich parametrach, a także metod szacowania lub stymulowania procesów rzeczywistych, natomiast obiektywizm zawarty jest w fakcie consensusu w środowisku zarządzających finansami, co do powszechnie przyjmowanych założeń o rozkładach w praktycznie stosowanych procedurach i algorytmach decyzyjnych.
Niepewność jest czymś innym niż ryzyko. Problem niepewności występuje w rzeczywistości ekonomicznej, kiedy podejmujący decyzję nie znają konsekwencji swojego wyboru. Niepewność w projektach inwestycyjnych klasyfikuje się na ogół według źródła pochodzenia, które może wynikać ze:
=> zmiany preferencji - w wypadku inwestycji - użytkowników, w rezultacie wpływające na strukturalne zmiany popytu w różnych gałęziach;
=> zmian w postępie technicznym (bardziej prawdopodobne w przemysłach komplementarnych, mniej w metodach tworzenia infrastruktury);
=> indywidualnej reakcji użytkowników na konieczność przystosowania się do zmian wywołanych rozwojem infrastruktury;
=^> działania sił przyrody niemożliwych do przewidzenia, a nawet do rozpoznania.
Niepewność interpretuje się niekiedy przez wprowadzenie czynnika czasu, dla którego przyszłość nie jest znana, więc o wystąpieniu zdarzeń lub zjawisk można twierdzić z
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
określonym prawdopodobieństwem1. Dla całego szeregu przewidywanych skutków zdarzeń nie zawsze jest możliwe określenie prawdopodobieństwa wystąpienia każdego z nich. Gdzie można określić którekolwiek z trzech rodzajów prawdopodobieństwa: matematyczne, statystyczne lub szacunkowe, tam występuje ryzyko. Inaczej mówiąc, ryzyko definiuje się w kontekście znajomości rozkładu prawdopodobieństwa. Miary prawdopodobieństwa są jednocześnie miarami ryzyka. Prawdopodobieństwo zdarzenia zawiera się 0<p<l\ jeśli prawdopodobieństwo zdarzenia W wynosi p, to ryzyko jego niewystąpienia wynosi (l-p). Jeśli niemożliwe jest określenie prawdopodobieństwa jakiegoś zdarzenia, to działalność odbywa się w warunkach niepewności. Niejednokrotnie w procesie podejmowania decyzji można oszacować wielkości zdarzeń (stopa zwrotu z inwestycji w różnych wariantach projektu), ale niemożliwe jest przypisanie im prawdopodobieństwa. Ryzyko można określić jako mierzalną niepewność. W literaturze spotyka się zamienne stosowanie obu pojęć. Przyczyną są dwa dominujące w ekonomii nurty postrzegania niepewności i ryzyka. Pierwsze wywodzi się z teorii F. Knighta, który wprowadził rozróżnienie między niepewnością i ryzykiem w zależności od możliwości pomiaru . Definicję ryzyka F. Knighta rozwinął G.S.L. Shackle, uzupełniając rozróżnienie z niepewnością o eksperyment podzielny i niepodzielny . Przez eksperyment rozumie działanie w warunkach niepewności rezultatu. Jeśli ostateczny wynik eksperymentu ustala się przez sumę wyników poszczególnych, dostatecznie licznych, prób przeprowadzonych w bardzo zbliżonych warunkach, tak że można zastosować rozkład prawdopodobieństwa na podstawie serii prób traktowanej jako całość, to eksperyment jest podzielny. Wówczas można mówić o ryzyku. Gdy eksperyment dotyczy jednej -niepodzielnej na elementarne i podobne działania - obserwacji, to jest niepodzielny i towarzyszy mu niepewność.
Drugi nurt rozwinął J.M. Keynes, który nie podtrzymywał zdecydowanego rozróżnienia między niepewnością i ryzykiem ze względu na odrzucenie prognozowania na podstawie częstości występowania minionych zdarzeń; traktował niepewność jako bardziej istotny element podejmowania decyzji niż przydatność matematycznego prawdopodobieństwa do szacowania przyszłych wielkości ekonomicznych4. J.M.Keynes twierdził, że nie można znaleźć żadnej naukowej podstawy by oszacować jakiekolwiek prawdopodobieństwo zmian cen, stóp procentowych czy starzenia się nowych technologii3.
Chociaż obaj ekonomiści upatrywali źródła niepewności w nieracjonalności ludzkiej natury, to ich rozważania zainspirowały rozwój teorii w przeciwnych kierunkach. Pierwszy nurt w kierunku kontroli ryzyka za pomocą teorii gier, która podaje własną definicję niepewności. Zgodnie z nią ludzie maksymalizujący użyteczność są świadomi działań innych osób, niemal każdą decyzję podejmują na podstawie licznych negocjacji przeprowadzanych w celu zmniejszenia niepewności, uzgadniając między sobą to, czego wzajemnie oczekują od siebie. Drugi - ku doskonaleniu metod ilościowych zmierzających do kontroli ryzyka6.
' Zob. J. Hirshleifer: Investment Decision under Uncertainty - Choice-Theoretic Approaches, „The Quarterly Journal of Economics" vol. LXXIX, no.4/1965 i E. Smaga: Ryzyko i zwrot w inwestycjach, Fundacja Rozwoju Rachunkowości w Polsce, Warszawa 1995, s. 8-9.
2 F. Knight podkreśla, że najistotniejszą kwestią w zrozumieniu problemu jest niedoskonała wiedza o przyszłości
w aspekcie konsekwencji zmiany warunków rynkowych, a nie samej zmiany. F. Knight: Risk, Uncertainty and
Profit, London 1946, s. 197-263.
3 G.L.S. Shackle: The Naturę and Role of Interest, [w:] Surveys of Economic Theory, Resource Allocation, New
York 1968
4 J.M. Keynes: Ogólna teoria zatrudnienia, procentu i pieniądza, PWN, Warszawa 1985, s. 172-173.
5 Swoje poglądy na temat niepewności J.M. Keynes wyłożył w odpowiedzi na dyskuję nad „Ogólną teorią" w:
The General Theory, „Gjuarterly Journal of Economy" vol. LI, no. 1/1937.
6 Dokładny i niekonwencjonalny opis teorii zajmujących się niepewnością i ryzykiem od J. Neumanna i O.
Morgensterna poprzez H. Markowitza, J. Nasha, teorię pochodnych instrumentów finansowych na teorii chaosu
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
W literaturze polskiej spotyka się krytykę rozróżniania ryzyka i niepewności na podstawie kryterium mierzalności, wykazującą, że jest ono nieprecyzyjne i bezużyteczne. W zamian proponuje się interpretację, że ryzyko jest kategorią związaną z działaniem zależnym funkcyjnie od informacji i oznacza „zmienność rezultatu zbioru okoliczności, który może wystąpić w danym miejscu i czasie7". Uzależnienie ryzyka od dostępu do informacji jest słusznym kierunkiem rozumowania wykraczającym poza rozkład prawdopodobieństwa, lecz nie oznacza odejścia od głównego nurtu definiowania tych pojęć. Wyznaczenie funkcyjnej zależności jest także pomiarem ryzyka.
Istota ryzyka sprowadza się do określenia prawdopodobieństwa wystąpienia konsekwencji dokonanego wyboru, które można potraktować na dwa sposoby, znane w literaturze jako obiektywny („częstościowy" lub „klasyczny") i subiektywny („stopnie zaufania" lub Bayesa8).
Prawdopodobieństwo ma charakter obiektywny, gdy uzyskuje się je albo z dotychczasowego doświadczenia, albo z podobnych projektów i powtarzających się zdarzeń (interpretacja częstościowa i jednakowa u każdego eksperta lub decydenta). Najbardziej pożądana jest możliwość zastosowania prawa wielkich liczb do szacunku rozkładu prawdopodobieństwa uzyskania zwrotu z projektu inwestycyjnego, jako że warunki niezbędne do działania tego prawa sprawiają, że metody statystyczne (oczekiwana wartość) stanowią satysfakcjonujące kryterium podejmowania decyzji.
Subiektywny charakter prawdopodobieństwa ma związek z niepowszechnym występowaniem prawa wielkich liczb w życiu gospodarczym (przede wszystkim brak doświadczenia w przebiegu nowego zjawiska oraz niedoskonała informacja zarówno pod względem ilości, jak i jakości). Wówczas podejście częstościowe do prawdopodobieństwa jest niewłaściwe; polega się na ekspertyzach, opiniach czy nawet intuicji o prawdopodobieństwie zdarzeń (różna interpretacja jednostkowych zdarzeń przedstawiana przez poszczególne jednostki), a nie na obiektywnych danych.9 Tutaj prawdopodobieństwo jest interpretowane raczej jako stopień wiary lub przekonania o możliwości wystąpienia zdarzenia i do takiej koncepcji muszą być dostosowane liczbowe wartości poszczególnych stopni. Według A. K. Dasgupty i D.W. Pearce'a koncepcja prawdopodobieństwa subiektywnego powinna zawierać następujące elementy:
funkcjonalne połączenie stopni wiary wystąpienia zdarzenia z przygotowaniem do
radzenia sobie z nim10;system aksjomatów dających się pogodzić z wyborem między niepewnymi
perspektywami11.
skończywszy znajdzie czytelnik w dziele P.L. Bernsteina: Przeciw bogom. Niezwykłe dzieje ryzyka, Wig Press, Warszawa 1997, s. 207-308.
7 Obszerny przegląd literatury polskiej odnośnie niepewności i ryzyka zawiera praca M. Wierzbińskiej: Ryzyko
w gospodarce rynkowej, Wydawnictwo Uniwersytetu Marii Curie-Skłodowskiej, Lublin 1996, s. 12-13.
8 T. Bayes podniósł fundamentalne problemy prawdopodobieństwa subiektywnego. Klasyfikacje przyjęto za
A.K. Dasgupta, D. W. Pearce: Cost-Benefit Analysis: Theory and Practice, London 1981, s. 177.
9 O teoriach prawdopodobieństwa zob. P.G. Moore: Ryzyko w podejmowaniu decyzji, PWE, Warszawa 1975,
s.29-36.
10 Robienie zakładów jest tradycyjnie rozpatrywane jako rodzaj działalności, do której odnoszą się stopnie wiary.
Zatem można próbować zmierzyć stopień czyjejś wiary w pewne zdarzenie poprzez zaproponowanie zakładu i
poszukiwanie najniższych różnic w - możliwych do zaakceptowania -przez tę osobę - stawkach gry. W takim
wypadku „prawdopodobieństwo" 1/4 odnosi się do stopnia wiary prowadzącego do zakładu 3 do 1. Przyjęcie lub
odrzucenie takich zakładów może być opisane jako wybór między niepewnymi perspektywami lub między
różnymi formami hazardu.
' W literaturze przywołuje się najczęściej systemy opracowane przez J. Neumanna i O. Morgensterna , F.P. Ramsey'a różniące się szczegółami, które J. Marschak uprościł do czterech aksjomatów:
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
Podejście to zawiera słabe punkty wynikające z pomiaru w jednostkach pieniężnych wygranej lub straty użyteczności, która jest większa przy stracie l jednostki pieniężnej niż w wygranej oraz z niewłaściwego wykorzystania algebraicznych praw prawdopodobieństwa (brak powtarzalnych zjawisk).
Ponieważ często prawdopodobieństwo jest kombinacją elementów obiektywnych i subiektywnych, stąd w literaturze przedmiotu na ogół nie dokonuje się analizy jego charakteru1 .
K.J. Arrow, podsumowując ówczesne osiągnięcia ekonomii i statystyki w zaadoptowaniu rachunku prawdopodobieństwa, stwierdził, iż „mimo że uzasadnienie posługiwania się kategoriami prawdopodobieństwa może wydawać się trudne, gdy zdarzenie zachodzi tylko raz, to z wyjątkiem interpretacji prawdopodobieństwa jako stopnia przekonania trudno byłoby obronić także przeciwne stanowisko" . Z tego wynika, iż w teorii ryzyka prawdopodobieństwo zajścia pojedynczego zdarzenia musi być także brane pod uwagę przy podejmowaniu decyzji. Ponadto zdaniem K.J. Arrowa twierdzenie Neumanna-Morgensterna. że niezależnie od stopnia skomplikowania struktury gry losowej zawsze można ją opisać za pomocą jednego rozkładu prawdopodobieństwa końcowych wyników, prowadzi do wniosku, że rozkład prawdopodobieństwa zdarzeń ma znaczenie nawet wtedy, gdy występuje tylko jedno zdarzenie, czyli każda definicja prawdopodobieństwa prowadzi do interpretacji „stopnia przekonania"14. To stanowisko umożliwia zrobienie następnego kroku przez W. Vickrey'a, który uważa, że jeśli dokonanie wyboru zawiera elementy ryzyka, to zachowanie podejmującego decyzję zmierza do określenia funkcji użyteczności możliwej do zinterpretowania „bezpośrednio w warunkach poświęcenia". Jednocześnie zapewnia, iż takie podejście precyzuje znaczenie zarówno funkcji użyteczności całkowitej, jak i użyteczności krańcowej oraz - co najistotniejsze - bezpośrednio może nawiązywać do problemów polityki społecznej.13 Zatem racjonalne zachowanie w tej płaszczyźnie można zdefiniować jako zachowanie możliwe do opisania przez matematycznie określoną maksymalizację oczekiwań.
Decydentowi, znającemu wartość każdego rezultatu, pozwoliłoby to ustalić rozkład użyteczności społecznej poszczególnych wariantów i przejść do wykorzystania statystycznej charakterystyki projektu, tj. obliczenia wartości oczekiwanej i wariancji16. Z punktu widzenia
kompletnego uporządkowania, o którym stanowią warunki uporządkowanie połączenia i przechodniości, tj.
istnieją zależności między preferencjami lub stanami obojętności co najmniej tak samo dobrymi w ocenie
decydenta;ciąglości zakładający, że jeśli istnieją trzy kombinacje x,y,z, z których x jest bardziej preferowana niż y, a y
bardziej niż z i istnieje taka kombinacja prawdopodobieństwa x i z, wobec której decydent jest obojętny, to jest
on również obojętny między nią i y,silnej niezależności stanowiący, że dopóki prawdopodobieństwo kombinacji z i x oraz x i y jest odpowiednio
takie samo, dopóty początkowa relacja obojętności wyboru między x i y nie powinna być zakłócana przez z;
4. wystarczającej liczby (co najmniej czterech) nieobojętnych kombinacji, umożliwiający udowodnienie
twierdzenia o oczekiwanej użyteczności. Por.:A.K. Dasgupta, D.W. Pearce: Cost-Benefit Analysis, wyd. cyt. s.
180.
12 Por. D.W. Pearce: Cost-Benefit Analysis, London 1983, s. 74.
13 K. J. Arrow: Eseje z teorii ryzyka, PWN, Warszawa 1979, s.33.
4 Tamże, s. 43 145.
15 K. J. Arrow: Eseje z teorii ryzyka, PWN, Warszawa 1979, s.33.
5 Tamże, s. 43 i 45.
15 W. Yickrey: Measuring Marginal Utility by Reactions to Risk, Public Economics, Cambridge 1994, s. 21.
6 Ten sposób argumentacji opiera się na wyprowadzeniu prawdopodobieństwa p, z użyteczności całkowitej
poszczególnych rezultatów zamierzenia f.i,. Wówczas Zp,p, -/.t interpretuje się jako pierwszy moment (wartość
oczekiwana) prawdopodobnego rozkładu użyteczności z danej decyzji. Drugi moment to miara dyspersji; jest
definiowany jako Zp, fa -p.)2 ( wariancja), a r-ty moment jako Zp, (/j, - u)r. W praktyce dwa pierwsze wystarczają
do dokonywania porównań. Zob. szerzej: A.K. Dasgupta, D.W. Pearce: Cost-Benefit Analysis: Theory and
Practice, London 1981, s. 177.
8
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
społeczeństwa jako podmiotu zainteresowanego w maksymalizacji dobrobytu społecznego, znaczenie ma duża liczba niezależnych, ale podobnych pod względem ryzyka inwestycji o charakterze publicznym i relatywnie niewielkim wpływie na produkt krajowy i konsumpcję, Ponieważ w danym roku niektóre projekty przynoszą korzyści większe od przewidywanych, inne mniejsze, nieistotne jest rozproszenie oczekiwanej wartości z inwestycji publicznych; ważniejsze w wyborze społecznym jest rozłożenie ryzyka „oczekiwanych użyteczności".
Konsekwencje niepewności i ryzyka dla podejmowania decyzji odnośnie inwestycji infrastrukturalnych są kwestią sporną dotyczącą szacowania aktywów o niepewnych przychodach według ich oczekiwanej wartości. Chodzi o to, że w zależności od posiadanych zasobów i ich użyteczności decydenci różnie szacują ich wartość, tj. powyżej lub poniżej ich oczekiwanej wartości. Na rynku kapitałowym nie inwestuje się w celu zmaksymalizowania zaktualizowanej wartości przychodów, lecz w celu zmaksymalizowania zaktualizowanej wartości przychodów z uwzględnieniem ryzyka. Spór dotyczy odpowiedzi na pytanie: czy dyskontowanie inwestycji o charakterze publicznym powinno być dokonywane w ten sam sposób co inwestycji prywatnych, biorąc pod uwagę niejednakową sytuację - względem ryzyka - rządu pod i inwestora .prywatnego.
Podejmowanie ryzyka to takie inicjowanie ciągów przyczynowo-skutkowych, kiedy nie wiadomo dokładnie, co się stanie, lecz wiadomo przynajmniej, co się stać może. Nie ma ryzyka wtedy, kiedy dosłownie wszystko jest możliwe (cokolwiek się zrobi, stanie się to impulsem do dowolnej, nawet najbardziej odległej, wręcz absurdalnie nie związanej z przyczyną, zmiany na świecie). Nie ma też ryzyka, gdy podmiot nie wie dosłownie nic, a więc wówczas, kiedy obszar możliwości byłby dlań nieskończony, rzecz jasna w sytuacji, gdyby ów podmiot przynajmniej to jedno w ogóle rozumiał.
Dlaczego podejmowane jest ryzyko? Dlaczego podejmujemy ryzyko w sytuacji, w której bez żadnego ryzyka można by dokonać wyboru innej, bezpiecznej drogi? Pytanie dotyczy sensowności wyboru sytuacji, w których dochodzi do potrzeby uporania się z ryzykownymi wyborami. Albo inaczej: aby wybierać w ramach ryzyka, trzeba wpierw zdecydować się na wybór samego ryzyka, jako podstawy późniejszych konkretnych wyborów. Ujęcie dotyczy generalnego tematu: czy wkroczyć w niebezpieczną sferę ryzyka koniecznego (gdzie nie ryzykować w zasadzie niepodobna), czy też pozostać w sferze spokoju i bezpieczeństwa, to drugie znaczenie wskazuje na przeciwieństwo ryzyka i odstąpienia od decyzji, czyli niedziałania. Czy można nie działać ryzykownie? Oczywiście można. Skoro można nie ryzykować, to cóż skłania człowieka, aby poddał się dobrowolnemu parciu w sferę zagrożenia i niepewności? Ryzyko jest wyposażone w wartość wyżej cenioną od tego, co łatwe, znane i bezpieczne, ponieważ oferuje odmienną strategię dochodzenia do pewnych wysoko cenionych wartości, niemożliwych do uzyskania na drodze znanej, pewnej i bezpiecznej. Walor ryzyka ma charakter instrumentalny; jest narzędziem i środkiem do celu.
Ryzyko i odpowiedzialność. Chociaż podjęcie ryzyka nie daje gwarancji, iż ten cel zostanie osiągnięty, to przynajmniej wyklucza ono sytuację najgorszą, mianowicie całkowita rezygnację z własnego, podmiotowego udziału w kreowaniu przyszłości (w określonym jej wycinku). Chcemy wszak, aby było lepiej, niż jest, wiedząc zarazem, iż niejednokrotnie nie ma innego wyjścia, jak tylko konieczność ryzykowania (aby nie pozostawać wciąż w punktach zerowych i kręcić się wokół nich w promieniu biernej, chciejskiej, bezskutecznej).
3. Indywidualne postawy wobec ryzyka
Ryzykowne działanie charakteryzuje się dwiema cechami:
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
prawdopodobieństwem (częstotliwość) wystąpienia określonego wyniku
(np. prawdopodobne odsetki z oszczędności na rachunku bankowym),skalą zmienności wszystkich możliwych wyników.
Grami nazywa się sytuacje, kiedy wyniki o pewnej wartości pieniężnej pojawiają się z różnym prawdopodobieństwem .
Rodzaje gier
Jeśli istnieje 50%-owa szansa zarobienia 1000 PLN, to znaczy, że istnieje jednocześnie 50%-we prawdopodobieństwo utraty tej kwoty pieniędzy (rzut monetą). Udział w takiej grze nie przynosi - przeciętnie rzecz biorąc - szansy na zarobienie pieniędzy. Stąd też taką grę nazywa się uczciwą. Czyli gra uczciwa to taka gra, w przypadku której zyski -przeciętnie rzecz biorąc - są równe zeru.
Jeśli szansa wygrania w/w sumy pieniędzy wynosiłaby 30%, a szansa przegrania 70%, to taką grę nazywa się nieuczciwą. Grając w nią -przeciętnie rzecz biorąc traci się pieniądze.
Gdyby sytuacja była odwrotna, tj. 70%- we prawdopodobieństwo wygranej i 30%- we przegranej, to gra byłaby korzystna, ponieważ udział w grze przeciętnie przyniósłby zysk.
Nie zawsze ludzie biorą udział w grach dobrowolnie. Przypuśćmy, że ktoś posiada domek letniskowy warty 20 tyś. PLN na skraju Borów Tucholskich. Niech prawdopodobieństwo włamania do niego i straty 10 tyś. PLN wynosi 10%, a prawdopodobieństwo tego, że do włamania nie dojdzie i właściciel ani nie straci, ani nie zyska wynosi 90%. Życie zmusza do udziału w takiej grze.
Z punktu widzenia gracza, któremu zależy na wygranej, jedną z najważniejszych cech gry jest jej wartość oczekiwana (WO), czyli suma jej wyników pomnożonych przez prawdopodobieństwo ich pojawienia się. Informuje ona o przeciętnym wyniku wielu partii tej
Wi = -1000 * 0,5 + 1000 * 0,5 = O zł. WO2 = -1000 * 0,7 + 1000 * 0,3 = - 400 zł. WO3 = 1000 * 0,7 + (- 1000) * 0,3 - 400 zł. WO4 = -10 000 * 0,1 + O * 0,9 - - 1000 zł.
Biorąc pod uwagę kryterium wyniku wartości oczekiwanej gry dzielą się na korzystne, uczciwe (sprawiedliwe) i niekorzystne (nieuczciwe).
Rodzaje gier Kryterium
wyniku wartości oczekiwanej
skala zmienności wyników
częstotliwość pojawiania się ich wartości skrajnych
korzystne (WO>0)
uczciwe (sprawiedliwe) (WO=0)
niekorzystne (nieuczciwe) (WO<0)
mniej ryzykowne
WGi < WG2 bardziej ryzykowne (WG2)
< WG2
10
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
Gra jest bardziej ryzykowna, im większy jest rozrzut jej wyników i im częściej pojawiają się wyniki najbardziej oddalone od wartości oczekiwanej gry.
Grając o 100 zł za pomocą rzutu monetą, może wypaść orzeł lub reszka z jednakowym prawdopodobieństwem 0,5. Wówczas WO, = 0,5 * 100 + 0,5 * (-100) = O
Podobnie, rzucając kostką, możemy wyrzucić parzystą lub nieparzysta liczbę oczek. Jeśli parzysta oznacza wygraną 1000 zł, a nieparzysta stratę 500 zł, to
WO2 = 0,5 * 1000 + 0,5 * (-500) = 250 zł.
Dla gry w rzucanie monetą wyniki 100 zł i -100 zł pojawiają się z takim samym prawdopodobieństwem jak dla gry w kości, ale wyniki są 1000 zł i - 500 zł. Druga gra jest bardziej ryzykowna niż gra pierwsza. Z tymi grami nie można porównać gry z domkiem letniskowym, ponieważ za duża jest różnica zarówno wyników, jak i prawdopodobieństw. Potrzeba bardziej precyzyjnej miary ryzyka związanego z udziałem w grze.
Za dokładną miarę zmienności wyników gry (ryzyko wność gry) uznaje się wariancję gry (WG). Jest ona sumą podniesionych do kwadratu odchyleń wyników gry od jej wartości oczekiwanej, zważonych prawdopodobieństwem wystąpienia tych wyników, czyli
WG = £ D, (ws - WO)2 , gdzie:
s=\
ws -wynik gry, na - prawdopodobieństwo ich wystąpienia.
W przypadku gry w rzucanie monetą o 100 zł, której wartość oczekiwana WO = O, wariancja gry wynosi:
WG, = 0,5 (100 zł)2 + 0,5 (-100 zł)2 = 0,5*10 000 zł + 0,5*10 000 zł =
= 5000 zł + 5000 zł = l O 000 zł
W gry w kości, której wartość oczekiwana WO = 250, wariancja tej gry równa się
WG2 = 0,5 (1000 zł - 250 zł)2 + 0,5 (-500 zł - 250 zł)2 =
= 281 250 zł + 281 250 zł = 562 500 zł.
Dla gry w letnisko, której wartość oczekiwana wynosi - 1000 zł, wariancja gry równa się: WG3 = 0,9 (0+1000 zł)2 + 0,1(-10 000 zł + 1000 zł)2 = 900 000 zł +8 100 000 zł =
= 9 000 000 zł.
Wynika stąd, że gra w kości jest bardziej ryzykowna od gry w rzucanie monetą, lecz mniej ryzykowna od gry w domek letniskowy.
Ekonomiści dzielą ludzi - ze względu na stosunek do gry uczciwej - na:
• unikających ryzyka (niechętne ryzyku) - nie wezmą dobrowolnie udziału w grze uczciwej bo oznaczałoby to wzięcie na siebie pewnego ryzyka, tymczasem powstrzymanie się od gry nie wiąże się z żadnym ryzykiem. Osoby niechętne ryzyku może skłonić do gry dopiero dodatnia wartość oczekiwana; wybiorą wówczas grę mniej ryzykowną. Przy czym nie chodzi tu wcale o niechęć do hazardu. Jeśli szansę na wygraną są dostatecznie duże, to nadzieja na prawdopodobne zyski pokona naturalną niechęć do ryzyka. Wymagana wysokość wartości oczekiwanej zależy od stopnia niechęci do ryzyka. Im bardziej dana jednostka unika ryzyka, tym większe muszą być szansę wygranej ;
11
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
neutralne - nie zwracają uwagi na stopień rozproszenia możliwych wyników gry; jest
im wszystko jedno, jakim ryzykiem jest obarczona wybrana gra. Decyzję o rozpoczęciu
gry podejmuje jedynie wtedy, gdy szansę na osiągnięcie zysków przeważają. Chociaż
każdy uczestnik gry naraża się na niebezpieczeństwo przegranej, a przegrane mogą
powtarzać się, osobę neutralną wobec ryzyka interesuje jedynie to, czy - przeciętnie
rzecz biorąc - uczestnictwo w grze przyniesie jakieś zyski;skłonnych do ryzyka (lubiące ryzyko) - podejmą wyzwanie nawet wtedy, gdy według
ścisłych matematycznych obliczeń prawdopodobieństwo przegranej przeważa, czyli
zawsze wybiorą grę bardziej ryzykowną. Im silniejsze jest zamiłowanie do ryzyka,
tym większe musza być szansę przegranej, aby zrezygnowali z gry. Osoba, która lubi
ryzyko zagra w grę sprawiedliwą, ponieważ powstrzymanie się od gry oznacza brak
ryzyka, natomiast udział w grze z wartością oczekiwaną równą zeru jest ryzykowny. Ze
względu na swoją skłonność do ryzyka osoby takie zaakceptuje nawet grę o ujemnej
wartości oczekiwanej. Dopuszczalny poziom ryzyka zależy oczywiście od stopnia jej
zamiłowania do ryzyka.
Badania empiryczne ujawniają, że ludzie nie lubią ryzyka. Obroty kasyn gier i wpływy z loterii, choć duże, nie dorównują obrotom firm ubezpieczeniowych. Ubezpieczenie jest przeciwieństwem hazardu.
Załóżmy, że ktoś posiada dom o wartości 500 000 PLN i że prawdopodobieństwo utracenia go wskutek pożaru lub powodzi wynosi 10%. Tym samym szansę utrzymania dotychczasowego stanu posiadania (500 000 PLN) są równe 90%, zaś szansę stracenia wszystkiego wynoszą 10%. Życie zmusza do przyjęcia tego zakładu. Przeciętnie właściciel uzyska 450 000 PLN, czyli 90% od sumy 500 tyś. zł plus 10% od zera. Firma ubezpieczeniowa oferuje ubezpieczenie pełnej wartości domu za 100 000 PLN. Sumę tę należy wpłacić niezależnie od tego, czy dom spali się, czy też pozostanie nienaruszony. Natomiast jest ona zobowiązana do wypłacenia odszkodowania w wysokości 500 000 zł tylko wtedy, gdy dom spłonie lub zostanie zalany. A zatem, bez względu na to, czy dom spłonie, czy nie, wartość majątku wyniesie 400 000 zł.
Postawy ludzi wobec ryzyka
Typ człowieka |
Decyzja o udziale w grze |
Ubezpieczenie przy niekorzystnych stawkach |
Unikający ryzyka |
Aby zgrać potrzebuje przewagi szans na wygraną |
Wykupi polisę |
Neutralny wobec ryzyka |
Nie zagra, gdy widoki na wygraną są niekorzystne |
Nie wykupi polisy |
Skłonny do ryzyka |
Zagra nawet wtedy, gdy prawdopodobieństwo przegranej przeważa |
Nie wykupi polisy |
Czy dom zostanie ubezpieczony? Towarzystwo ubezpieczeniowe wykorzystuje tę sytuację i w ten sposób zarabia pieniądze. Jeśli właściciel nie skorzysta z jego oferty, jego średni wynik wyniesie 450 tyś. zł. Jednak wynik rzeczywisty może być równy 500 tyś. lub zeru. Ubezpieczenie gwarantuje pewny wynik w wysokości 400 tyś. zł. Osoba neutralna odrzuci ofertę, ponieważ zgodnie z kalkulacją matematyczna bardziej opłaca się podjęcie ryzyka, że dom spłonie lub zostanie zalany. Oferta zostanie również odrzucona przez osobę skłonną do ryzyka, ponieważ ubezpieczenie nie daje szans na wygraną, a zabiera
12
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
przyjemność odczuwania ryzyka. Osoba z awersją do ryzyka zdecyduje się na ubezpieczenie, bo suma tracona w stosunku do przeciętnego wyniku (50 tyś. zł) nie wydaje się zbyt wygórowaną ceną za uniknięcie możliwej katastrofy.
Niektórzy twierdzą, że przyczyną niechętnego nastawienia ludzi do ryzyka jest ich stosunek-do bogactwa. Kolejne porcje pieniądza (AMi = AM2 = AM3 ...) w coraz mniejszym stopniu (odpowiednio: o AUj > AU2 > AU3 ...) zwiększają użyteczność całkowitą tego, kto je dostaje. Zmiana użyteczności całkowitej spowodowana wzrostem dochodu o daną, stałą porcję, czyli użyteczność krańcowa zmniejsza się w miarę wzrostu dochodu. Najbardziej użyteczne produkty zostają nabyte szybko, za pierwsze porcje dochodu.
użyteczność całkowita
Malejąca krańcowa użyteczność pieniądza
użyteczność całkowita
! (AU,)>(AU2)
AU
AU2 AU
AU,
O AM, AM2 AM3
bogactwo
O M, M* M2
bogactwo
Skoro użyteczność krańcowa dochodu pieniężnego maleje, to utrata danej sumy pieniądza powoduje spadek użyteczności całkowitej, który jest większy od przyrostu użyteczności całkowitej spowodowanego dodatkowym dochodem takiej samej wielkości. Utrata kwoty MiM* powoduje obniżenie się użyteczności całkowitej o AUi, natomiast przyrost dochodu o kwotę M2M*, równą M|M*, podnosi użyteczność tylko oAU2. Malejąca krańcowa użyteczność sprawia, (AUi) > (AU2). Wartość bezwzględna straty jest większa od wartości bezwzględnej korzyści. Gra sprawiedliwa w kategoriach pieniężnych okazuje się niekorzystna w kategoriach użyteczności. Wygrana pewnej kwoty pozwoli na zakup jakiejś ilości dóbr luksusowych, przegrana zaś zmusi do zrezygnowania z zakupu znacznej ilości dóbr podstawowych. To właśnie dlatego ludzie unikają gier sprawiedliwych, czyli są niechętni ryzyku! Wyjątek może stanowić udział w okazjonalnych grach o niskich stawkach, prowadzonych dla czystej przyjemności. Gra zapewniająca równe szansę wygrania lub przegrania określonej kwoty pieniężnej nie jest grą uczciwą z punktu widzenia użyteczności.
Podejmowanie ryzyka zależy od dwóch czynników: uczucia przyjemności lub przykrości towarzyszącemu ryzyku.
Z dotychczasowej analizy wynikają dwa wnioski:
13
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
osoby unikające ryzyka są skłonne poświęcić część swoich zasobów, aby je
zmniejszyć (rozwój sektora ubezpieczeń),jednostki, które biorą na siebie ryzyko, muszą otrzymać za to odpowiednie
wynagrodzenie.
W praktyce, inwestorzy rzadko są hazardzistami i niemal zawsze przedkładają szansę mniejszych zysków (lub mniejszych strat) nad szansę większych zysków (lub większych strat). Wiele rodzajów działalności ekonomicznej to odpłatne usługi tych, którzy mniej boją się ryzyka, polegające na przejmowaniu ryzyka i świadczone na rzecz tych, którzy bardzo nie lubią niepewności.
Skłonność społeczeństwa do ryzyka
Użyteczność Użyteczność
U(B2)
U(B0) EU(B)
U(B,)
O B, B* Bo
B2
B, Bo B* B2
Gdyby uzyskanie korzyści z zamierzenia bi lub 5? były uznane za pewne, wówczas
użyteczność wynosiłaby odpowiednio U(Bi) lub u(bt).
Możliwość pojawienia się obu poziomów korzyści z niejednakowym, lecz określonym
prawdopodobieństwem p/ i p-2 pozwala obliczyć oczekiwaną wartość EU wyrażoną
równaniem:
EU = piU(Bi) + p2U(Bi), którego graficzna postać kryje się za odcinkiem XY. Przy rozkładzie
prawdopodobieństwa pi/p2 wartość oczekiwana znajduje się tam, gdzie B}B(/BoB2=pi/p2 (E}-
Prawidłowością jest wyższa użyteczność w warunkach pewności (krzywa U(B) niż
użyteczność oczekiwana dla każdego poziomu korzyści o prawdopodobieństwie zdarzenia
mniejszym od jedności (krzywa XY) dla społeczeństwa niechętnego ryzyku (a).
Odwrotna prawidłowość występuje w odniesieniu do społeczeństwa skłonnego do ryzyka (b).
Tutaj oczekiwana użyteczność korzyści jest większa od użyteczności jej wartości
oczekiwanej. Społeczny koszt ponoszenia ryzyka mierzy się odcinkiem bo - B*, gdzie B*
interpretuje się jako korzyści w warunkach pewności przy uzyskanej oczekiwanej
użyteczności dla bi i B2.
„Informacja, którą posiadasz, nie jest informacją, której szukasz Informacja, której szukasz, nie jest informacją, której potrzebujesz Informacja, której potrzebujesz, nie jest informacją, którą możesz uzyskać Informacja, którą możesz uzyskać, kosztuje więcej niż możesz za nią zapłacić."
14
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
Rodzaje ryzyka
Jeśli można zmierzyć prawdopodobieństwo wystąpienia pewnego zdarzenia z przedziału wartości <0,1>, to im wyższa zmienność rezultatu, tym wyższe ryzyko. Z tego wynika pierwsze podejście do klasyfikacji ryzyka na:
obiektywne (prawdopodobieństwo otrzymania rezultatu w danych
warunkach i czasie),subiektywne, będące efektem subiektywnych szacunków osób, które muszą
się na nie przygotować.
Innymi słowy, ta sama sytuacja daje różne wyniki szacunków zależnie od zgromadzonych doświadczeń przez ludzi narażonych na występowanie identycznego ryzyka.
Wyróżnia się następujące elementy ryzyka:
przedmiot - wartości materialne (kapitał rzeczowy) i niematerialne (marka firmy,
zaufanie klientów do firmy),wszelkie siły sprawcze, które mogą spowodować wystąpienie strat (nieprzewidzianych
zysków), które można podzielić na:
naturalne (trzęsienia ziemi, powodzie, epidemie), spowodowane przez ludzi (kradzież, wandalizm, niedbalstwo),
ekonomiczne, które są związane z takimi zjawiskami jak recesja, inflacja, przemiany w poziomie rozwoju technologicznego, zmiany gustów konsumentów.
Biorąc to kryterium pod uwagę można wydzielić:
^ ryzyko czyste, gdy można ponieść tylko szkodę, natomiast wykluczone jest osiągnięcie korzyści (np. kradzież, w wyniku której ponosi się jedynie straty). Ma charakter rekurencyjny, co oznacza, że przy założeniu pewnych okoliczności istnieje prawdopodobieństwo jego wystąpienia. Tym samym jest ono stosunkowo łatwe do przewidzenia.
^ ryzyko spekulacyjne, gdy występuje prawdopodobieństwo poniesienia strat i osiągnięcia korzyści (wprowadzenie nowego produktu na rynek- pozytywnym przykładem są komputery osobiste, a niekorzystnym - samolot „Concorde"),
• potencjalny wpływ strat (zysków) i szkód na sytuację finansową.
Ze względu na wszechobecność występowania ryzyka w działalności gospodarczej wyróżnia się:
•J* ryzyko wewnętrzne - pojawia się od momentu pojawienia się pomysłu założenia firmy i jej rozwoju. Można nad nim panować podejmując decyzje dotyczące na przykład wielkości inwestycji,
*J* ryzyko zewnętrzne - uzależnione jest od rynku, od tego, co robi konkurencja lub od polityki rządu.
Klasyfikacja ryzyka bankowego jest trudna ze względu na złożone funkcje banków.
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
Rodzaje ryzyka w poszczególnych obszarach działania banków |
Obszar wartości |
Ryzyko utraty płatności, ryzyko kredytowe, ryzyko zmiany stopy procentowej, ryzyko w obrocie papierami wartościami, ryzyko kursowe, ryzyko zmiany wartości składników majątkowych, ryzyko stosowania innowacji finansowych |
Obszar techniczny |
Ryzyko niesprawności technicznej, ryzyko niesprawności organizacyjnej, ryzyko kadrowe. ryzyko pominięcia ważnych informacji, ryzyko finansowania nowych technologii |
Obszar strategiczny |
Ryzyko kraju, ryzyko związane ze zmianami w przepisach prawnych (np. podatkowych) |
Źródło: A. Kropielnicka: Analiza ryzyka \v controllingu, „Bank i Kredyt'1' nr 7/1993. Trzeba też wspomnieć o klasyfikacji ryzyka walutowego, które dzieli się na:
ryzyko kursowe - ważne wyróżnienie pozycji walutowej zajmowanej przez
bank do koszyka walutowego będącego podstawą wyliczenia kursu złotówki,
tak aby w każdym razie można było określić, jaka część dochodów lub strat
związana ze zmianą wartości złotego, a jaka wynika z ruchu kursu walut
obcych między sobą.ryzyko kredytowe - związane z niebezpieczeństwem, że kontrahent banku nie
będzie chciał lub nie będzie mógł z powodów wewnętrznych wypełnić
ciążących na nim zobowiązań, przy czym ryzyko to obejmuje wszystkie
możliwe operacje, a nie tylko kredyty i pożyczki. W szczególności bank
wykonując transakcje wymiany walutowej, w których przesyła pieniądze, jako
pierwszy ponosi ryzyko kredytowe.ryzyko kraju - związane z możliwością, że kontrahent banku nie będzie w
stanie wypełnić swych zobowiązań wskutek sytuacji w jego kraju.ryzyko transakcji - obejmuje straty, jakie bank może ponieść przy
wykonywaniu transakcji dewizowych na skutek różnego rodzaju
niedokładności, pomyłek i oszustw.ryzyko stopy procentowej - związane z zagrożeniem, że zmiana stopy
procentowej waluty obcej spowoduje straty banku.ryzyko płynności walutowej - związane z zagrożeniem, że bank nie będzie w
stanie wykonać swoich zobowiązań wskutek braku środków płynnych w
walutach obcych.
Każdy rodzaj ryzyka walutowego wymaga - ze względu na swoją specyfikę -odmiennego traktowania. NBP ustalił wspólny dla wszystkich rodzajów ryzyka schemat ich nadzorowania. Schemat ten wymaga funkcjonowania podziału całości nadzorowania danego ryzyka na następujące części:
o mierzenie - polegające na ustaleniu jednoznacznych zasad określenia wielkości ryzyka,
16
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
o raportowanie - obejmujące tworzenie, sprawdzanie i przesyłanie sprawozdań dotyczących ponoszonego ryzyka,
o limitowanie - polegające na bieżącym określeniu, jaki poziom danego ryzyka bank może zaakceptować,
o zarządzanie - obejmujące działanie konieczne do zmniejszenia lub usunięcia istniejącego zagrożenia,
o kontrola - polegająca na wykrywaniu wszelkiego rodzaju nieprawidłowości.
Źródła i rodzaje ryzyka w ocenie projektu inwestycyjnego
Czynniki makroekonomiczne
Czynniki mezoekonomiczne
Czynniki mikroekonomiczne
Źródła ryzyka
Rodzaje ryzyka
w ocenie inwestowania
Kryteria:
geograficzne częstotliwości skutków decyzji efektywnego doboru źródła finanso-
występowania inwestycyjnej projektu wania
w globalnej strategii
Ryzyko
regionu
kraju
międzynaro
dowe
Ryzyko
systema
tycznespecyficz
ne
Ryzyko
projektu
firmy
rynkowe
właścicielisektora
Ryzyko
operacyjne
finansowe
Ryzyko
zerowe
ukryte
jawne
całkowitej
niewypłacal
ności
Źródło: E. Ostrowska: „Ryzyko inwestycyjne", s. 29
Wielokryterialna identyfikacja rodzajów ryzyka ma istotne znaczenie w aspekcie możliwości jego uwzględnienia w rachunku efektywności inwestycji.
Kryterium geograficznej dywersyfikacji kapitału związane jest z przepływem kapitału w ujęciu geograficznym i obejmuje:
> ryzyko inwestycyjne regionu zależy od zasobów naturalnych, warunków lokalizacyjno-komunikacyjnych i możliwości pozyskania siły roboczej,
17
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
ryzyko kraju, które ma wpływ na decyzje inwestorów zagranicznych. Bierze
się w nich pod uwagę: stabilność gospodarki (strajki, zmienność władzy,
inflację, deficyt budżetowy, koszty pracy), sytuację prawno-społeczną (jasność
i stabilność prawa, nastroje społeczne), stan infrastruktury społeczno-
ekonomicznej,ryzyko międzynarodowe wynika ze światowych tendencji globalizacji i
internalizacji gospodarki.
Ze względu na kryterium częstotliwości występowania danego ryzyka wyróżnia się:
ryzyko systematyczne (tzn. rynkowe, stałe lub niedywersyfikowalne), którego
przyczyną są czynniki ogólnogospodarcze i losowe (np. inflacja i wojna).
Dotyczy ono wszystkich realizowanych projektów inwestycyjnych, przy
założeniu uwzględnienia różnej wrażliwości projektów na to ryzyko. Ryzyko
systematyczne odnosi się do tej części zysku osiągniętego z danej inwestycji,
której zmiany są spowodowane przez czynniki wpływające na całą
gospodarkę. Dywersyfikacja nie może wyeliminować tego ryzyka, stąd jest
ono podstawową determinantą premii z tytułu ryzyka dla poszczególnych
projektów inwestycyjnych. Ta premia wynika z różnicy między oczekiwaną
(wymaganą) stopą zwrotu osiągniętą w czasie eksploatacji inwestycji a stopą
wolną od ryzyka.ryzyko specyficzne (nierynkowe, zmienne, dywersyfikowlane), którego
źródłem są czynniki mezo - i mikroekonomiczne. Dotyczy ono konkretnych
projektów, a nawet ich wariantów i scenariuszy.
Kryterium częstotliwości występowania ryzyka inwestycyjnego
ryzyko a
oczekiwana stopa zwn
^ |
^ k 1 |
r |
ryzyKO specyficzne |
ryzyko całkowite T |
f |
ł i |
k ryzyko systematyczr r |
stopa zwrotu
W ramach kryterium skutków decyzji inwestycyjnej w globalnej strategii przedsiębiorstwa można wyodrębnić:
> ryzyko projektu inwestycyjnego, które wynika ze skali trafności założeń technicznych i ekonomiczno-finansowych tego projektu. Rodzaj projektu inwestycyjnego jest nośnikiem rodzaju ryzyka. Przyjmuje się, że największe ryzyko towarzyszy nowym przedsięwzięciom inwestycyjnym zmierzającym do wejścia na nowe rynki i oferowania nowych produktów. Najmniejsze -charakteryzuje inwestycje odtworzeniewo-modernizacyjne. W tym wypadku inwestor ma większą^ sprawdzoną wiedzę odnośnie do warunków realizacji projektu inwestycyjnego;
18
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
> ryzyko przedsiębiorstwa zamierzającego realizować nową inwestycję zazwyczaj nie jest takie samo jak ryzyko inwestycji. Ryzyko przedsiębiorstwa zależy od relacji między korzyściami osiągniętymi z realizacji danego projektu z korzyściami związanymi z eksploatacją majątku będącego w dyspozycji tego przedsiębiorstwa. Miarą tego ryzyka jest wpływ projektu na zmienność jego zysków, ponieważ jest ono oceniane jako ryzyko całego portfela inwestycyjnego tego przedsiębiorstwa z pominięciem dywersyfikacji portfeli akcjonariuszy;
5> ryzyko rynkowe właścicieli przedsiębiorstwa, czyli właścicieli kapitału, jest związane z ryzykiem systematycznym oraz ze skłonnością i preferencjami tych właścicieli do lokaty kapitału w różnych firmach. W granicach własnego ryzyka mogą oni preferować dywersyfikację inwestycji finansowych, np. metodą portfela zakupu akcji. Umiejętny dobór papierów wartościowych umożliwia budowę portfela o odpowiedniej stopie zysku i wymaganym minimalnym ryzyku. Miarą omawianego ryzyka (ryzyko beta) ocenianego z punktu widzenia inwestującego w akcje i mającego zróżnicowany portfel jest współczynnik beta projektu. W modelu wyceny aktywów finansowych konkretny współczynnik beta to miara stopnia, w jakim zyski z danej akcji zmieniają się wraz ze zmianami całego rynku papierów wartościowych.
5> Ryzyko inwestycyjne sektora wynika z bardziej lub mniej uzasadnionego poglądu inwestorów, a także instytucji finansowych lub władz lokalnych, że przedsiębiorstwa danego sektora gospodarki mają możliwość uzyskać wyższą stopę zysku (lub są zagrożone niższą stopą zysku) w porównaniu do przedsiębiorstw innego sektora.
W rezultacie cztery rodzaje ryzyka są ze sobą skorelowane. Ryzyko pojedynczych projektów inwestycyjnych oddziałuje na ryzyko przedsiębiorstw, które ma wpływ na ryzyko rynkowe właścicieli. Z kolei suma poszczególnych firm należących do określonego sektora gospodarki determinuje szansę lub zagrożenia uzyskania oczekiwanej stopy zwrotu z inwestycji.
Kryterium efektywnego doboru projektu inwestycyjnego pozwala wyodrębnić:
^ ryzyko operacyjne związane ze zmianami w strukturze aktywów, tj. ze zmianami elementów majątku trwałego i obrotowego, a szczególnie elementów aktywów wpływających na zysk operacyjny firmy. Ryzyko to wynika ze stopnia wpływu zmian sprzedaży na kształtowanie się zysku operacyjnego;
>• ryzyko finansowe, które ma inny charakter, ponieważ dotyczy sposobu finansowania przedsięwzięcia inwestycyjnego. Jego wyznacznikami są zmiany w strukturze pasywów przedsiębiorstw, czyli wyników pionowej i poziomej struktury ich bilansu. Mogą to być zmiany w strukturze kapitału (własny i obcy) lub zobowiązań i należności. Z reguły duże inwestycje wymagają zaangażowania oprócz środków własnych, znacznego udziału środków obcych (kredyt bankowy, obligacje, leasing), co obciąża przedsiębiorstwo kosztami za korzystanie z obcego kapitału (odsetki). Duży udział kapitału obcego w globalnym majątku przedsiębiorstwa powoduje, że jego działalność związana jest z dużym ryzykiem finansowym. Przychody i zyski z inwestycji mogą być zbyt małe w relacji do pozostałych zobowiązań finansowych, a zatem mogą spowodować utratę płynności firmy (dźwignia finansowa).
19
pro f. Teresa Kamińska: Ryzyko w działalności gospodarcze WSB
stopa
ł
zwrotu

![]()
oczekiwana stopa zwrotu
ryzyko całkowite
ryzyko finansowe
\ryzyko operacyjn
czas
Dodatkowym kryterium klasyfikacji ryzyka inwestycyjnego mogą być źródła finansowania inwestycji, szczególnie zewnętrzne, np. kredyt bankowy. Z punktu widzenia źródła dopływu niezbędnego kapitału (kredytodawcy) istotne jest rozpoznanie i ustalenie znaczenia ryzyka:
zerowego, które występuje przy realizacji inwestycji finansowanych
kredytami, które są gwarantowane, np. przez państwo w przypadku inwestycji
prestiżowych. Ryzyko to dotyczy kredytu inwestycyjnego o
nierozpoznawalnym ryzyku, który otrzymują inwestorzy o niepodważalnej
solidności;ukrytego, dotyczącego głównie etapu przygotowania projektu (studium
możliwości i zagrożeń inwestycji oraz studium przedrealizacyjnego). Czyli
okresu pierwszych sygnałów rozwoju negatywnych tendencji, np. malejącej
płynności finansowej. Stąd udzielenie kredytu wymaga wnikliwego
controllingu. Ten rodzaj ryzyka powstaje w sytuacji, gdy konkretny projekt
jest już obciążony, ale bank nie ma podstaw (sygnałów) do oceny
ewentualnych strat. Zaistnieje ono, gdy prawdopodobieństwo wystąpienia strat
jest mniejsze od prawdopodobieństwa niewystąpienia tych strat;
^ jawnego, gdy prawdopodobieństwo poniesienia straty jest większe od prawdopodobieństwa uniknięcia straty. Jest to przypadek trwałych, negatywnych tendencji w przedsiębiorstwie inwestującym, a nie tendencji przejściowych, tak jak w wypadku ryzyka ukrytego. Kredytodawca przewiduje więc utratę części swojego kapitału finansowego;
> pewnego, czyli całkowitej niewypłacalności inwestora powstaje wraz z utratą
jego zdolności do obsługi zobowiązań. Z reguły prawdopodobieństwo obsługi
kredytu równa się zero, a więc dla banku jest to kredyt stracony.
Metody pomiaru ryzyka i niepewności
W praktyce nie istnieje powszechnie akceptowana metoda traktowania ryzyka, którą można byłoby zastosować w ocenie efektywności inwestycji. Problem mógłby być
20
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
rozstrzygnięty dzięki zastosowaniu metody rankingu projektów w zależności od oczekiwanej wartości i wariancji ich zwrotów z inwestycji.
Pomimo trudności pomiaru ryzyka w ogóle, wydaje się, że należy posługiwać się gdzie tylko możliwe zasadami wynikającymi z praw wielkich liczb, a w pozostałych wypadkach zarówno poszukiwać metod, jak i wykorzystywać tradycyjne podejścia wskazujące na prawdopodobieństwo wystąpienia ryzyka, bo jak twierdzi P.L. Bernstein: ..Istota kontrolowania ryzyka polega na maksymalizowaniu zakresu zagadnień, w odniesieniu do których jesteśmy w stanie, choćby w pewnym stopniu, przewidzieć skutki zdarzeń oraz minimalizowaniu tych obszarów, gdzie związki przyczynowo-skutkowe pozostają całkowicie poza naszą kontrolą i są nam nieznane"17.
* W takich sytuacjach, nazywanych niekiedy sytuacjami „całkowitej ignorancji", kryterium oczekiwanej użyteczności nie może być stosowane. Ekonomiści proponują wówczas narzędzia zbliżone do teorii gier, w której zakłada się, że decydent zna swoje zachowanie w każdym przypadku „stanu natury" i użyteczność wypłaty, jaką można uzyskać w rezultacie działania w warunkach każdego stanu. Inaczej mówiąc, można wnioskować, że zna macierz wypłat (patrz metody operacyjne).
W odniesieniu do wartościowania projektów inwestycyjnych sytuacja związana z określonym ryzykiem jest lepsza aniżeli wysoki stopień niepewności. Zakładając, że istnieje możliwość przekształcenia niepewności w ryzyko, w praktyce dokonywania wyboru wykształciły się następujące podstawowe grupy narzędzi przydatnych w różnych sytuacjach decyzyjnych:
metody korygujące polegające na ograniczeniu skutków niepewności przez
korektę (in plus lub in minus) parametrów wyjściowych w rachunku
efektywności inwestycji;analizę wrażliwości badając, jaki jest wpływ najważniejszych zmiennych na
podstawowe wskaźniki efektywności. Chodzi tu przede wszystkim o
stwierdzenie tempa zmian zaktualizowanej wartości netto NPV i/lub
wewnętrznej stopy zwrotu IRR, jeśli zmieniłyby się kolejno przychody, koszty
inwestycji i koszty eksploatacji (bada się poszczególne zmienne niezależne
przy pozostałych zmiennych ceteris paribus);metody probabilistyczne - statystyczne oceny ryzyka, w których
wykorzystuje się rachunek prawdopodobieństwa i metody statystyczne, takie
jak wartość oczekiwana (nadzieja matematyczna) i miary rozproszenia
(wariancję, odchylenie standardowe i współczynnik zmienności);metody symulacyjne dają możliwość zbadania wpływu wielu czynników
zależnych zmiennych na efektywność inwestycji oraz możliwość symulacji
ryzyka. Ważne w tym wypadku jest ustalenie parametrów symulacji i
złożonego cyklu symulacji. W odróżnieniu od analizy wrażliwości tutaj
badany jest wpływ różnych (wszystkich) kombinacji zmiennych na
efektywność projektu, a nie tylko każdej zmiennej z osobna;metody operacyjne, wśród których na uwagę zasługuje strategia gier. gdyż
wykorzystuje się ją w sytuacjach, kiedy nie ma możliwości ustalenia
prawdopodobieństw osiągania danego efektu.
L. Bernstein, op. cit. s. 174.
21
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
Generalnie wybór i zastosowanie omawianych metod zależy od preferencji decydentów w zakresie rozpoznawania dwóch skutków:
szans na osiągnięcie korzyści z tytułu realizacji projektu inwestycyjnego,
ryzyka popełnienia błędu (zagrożenia stratami) z tytułu błędnej decyzji
inwestycyjnej.
korekty parametrów rachunku
Korekta parametrów rachunku dotyczy zazwyczaj parametrów obciążonych ryzykiem istotnym dla inwestora, a szczególnie pełniących funkcję normatywu efektywności ekonomicznej. Weryfikacja parametrów polega na zwiększeniu lub zmniejszeniu wielkości lub wartości zmiennych, uprzednio skalkulowanych w rachunku. Celem jest tutaj określenie takiego poziomu zmiennych, który byłby bardziej realny w aktualnych warunkach realizacji projektu, przy uwzględnieniu danego horyzontu czasowego. Dzięki korekcie parametry obciążone ryzykiem stają się zmiennymi względnie pewnymi.
Do szczególnie narażonych na duże ryzyko należą następujące zmienne:
stopa procentowa (dyskontowa), stopa zysku. Ponieważ stopa procentowa (r)
równa się sumie stopy procentowej pozbawionej ryzyka r\, premii za ryzyko
inwestycyjne r2, spodziewanej stopy inflacji lub deflacji rlcj, tj. r = fi + r: + rjd,
to należy uwzględnić korektę wszystkich jej składników;okres zwrotu nakładów kapitałowych.
Przykład l Ocena ryzyka inwestycyjnego w sytuacji występowania dwóch zmiennych dyskontujących
Inwestor ocenia opłacalność realizacji projektu inwestycyjnego, który jest związany z poniesieniem nakładu inwestycyjnego w wysokości 9000 PLN. Okres realizacji i eksploatacji inwestycji wynosi 5 lat. Spodziewane salda przepływów pieniężnych (zyski) uzyskiwane w kolejnych latach tego okresu mają być następujące: 2000, 4000, 5000, 4000 i 4000. Stopa dyskontowa nie uwzględniająca ryzyka kształtuje się na poziomie 18%, a stopa z\viązana tylko z samym ryzykiem szacowana jest na poziomie 10%. W powyższej sytuacji, w ocenie efektywności inwestycji wykorzystującej dynamiczny rachunek wartości zdyskontowanej netto, należy zastosować metodę podwójnego dyskontowania (dwie zmienne dyskontujące).
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
lata |
Saldo przepływów (zysk/strata) |
Dyskontowanie bez ryzyka |
Dyskontowanie z ryzykiem |
||
|
|
współczynnik wartość dyskontujący zdyskontowna zmienna 18% |
|
||
|
|
|
współczynnik wartość dyskontujący zdyskontowana zmienna 10% |
||
0 |
-9000 |
1,000 |
-9000 |
1,000 |
-9000 |
1 |
2000 |
0,847 |
1694 |
0,909 |
1540 |
2 |
4000 |
0,718 |
2872 |
0,826 |
2372 |
3 |
5000 |
0,609 |
3045 |
0,751 |
2287 |
4 |
4000 |
0,516 |
2064 |
0,683 |
1410 |
5 |
4000 |
0,437 |
1748 |
0,621 |
1086 |
0-5 |
|
Razem wartość zdyskontowana NPV= 2423 |
Razem zdyskontowana wartość NPV = -305 |
||
analiza wrażliwości projektu inwestycyjnego
1. zasady rachunku wrażliwości
Zakładając inny poziom jednej lub kilku zmiennych w porównaniu do wcześniej przyjętych zmierza się do poszukiwania wartości krytycznych (granicznych) i marginesów bezpieczeństwa inwestycji. Chodzi o ustalenie progu rentowności i związanego z nim marginesu bezpieczeństwa inwestycji poprzez określenie minimalnej wielkości i wartości produkcji gwarantującej, przy przyjętej stopie procentowej, pokrycie kosztów z uzyskanych dochodów ze sprzedaży. Analizą tą obejmuje się również wyznaczenie granicznego okresu zwrotu zaangażowanego kapitału, czyli nakładów inwestycyjnych. Minimalny okres eksploatacji inwestycji powinien zagwarantować zwrot kapitału przy uwzględnieniu zmiany wartości siły nabywczej pieniądza.
Wyróżnia się dwa podstawowe warianty analizy:
wariant ze szczegółowymi zmiennymi wejściowymi
determinującymi przepływy środków pieniężnych (ceny
materiałów, stawki płac, wielkość produkcji, ceny produktów i
usług, stopień wykorzystania zdolności produkcyjnych itp.);wariant ze zagregowanymi zmiennymi wejściowymi, którymi
mogą być strumienie przepływu środków pieniężnych
(wydatków i przychodów) oraz skalkulowana stopa
dyskontowa.
Celem obu jest ustalenie stopnia wrażliwości wyniku rachunku NPV i IRR na zmiany konkretnych zmiennych. Dla każdego parametru, czyli istotnej zmiennej wejściowej, granicą bezpieczeństwa może być wartość bezwzględna lub wartość względna. W pierwszym przypadku jest to różnica między wartością maksymalną a najbardziej prawdopodobną albo między wymaganą wartością minimalną a najbardziej prawdopodobną. W drugim zaś jest to iloraz obliczonej wartości bezwzględnej granicy bezpieczeństwa i wartości najbardziej prawdopodobnej szacowanego elementu rachunku (iloraz może być pomnożony przez 100%).
23
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
Jednak zasady i mechanizmy jej zastosowania nie uwzględniają możliwości ustalenia prawdopodobieństw zmian wskaźników prawdopodobieństwa kształtowania się takiej, a nie innej wartości NPV. Jest to metoda tylko rozpoznawania ryzyka i prób jego ograniczania, a nie dokładnego pomiaru ryzyka.
Analiza wrażliwości projektu inwestycyjnego w warunkach zmian wielkości sprzedaży i przeciętnych kosztów zmiennych
a)sprzedaż
b) przeciętne koszty zmienne
NPV.
NPV
NPV0
-10%
10%
NPV0
-e-
-10% O
-t-
+10%
wahania zmiennej
Nachylenie krzywej jest wyznacznikiem ryzyka związanego z danym parametrem rachunku. Im kąt nachylenia jest większy, tym bardziej wrażliwa jest wartość NPV na wszelkie zmiany zmiennych wejściowych. Jeśli porównuje się kilka projektów (wariantów), to należy przedstawić wrażliwość na te same parametry na tym samym wykresie, ponieważ ułatwia to porównanie ryzyka tych projektów.
Wskaźnik bezpieczeństwa wb określa poziom wrażliwości danego projektu na spadek popytu; przyjmuje wartości o O do l, czyli im bliższy l, tym projekt bezpieczniejszy.
- BEP
IS,.
gdzie: ISm - maksymalna ilość sprzedanych produktów
BEP - liczba produktów, przy których projekt osiąga próg rentowności. Przykładowo, wb = 0,5 oznacza, że zmianę popytu nawet o 50% nie przyniesie strat ani zysków.
Próg rentowności dla produkcji wieloasortymentowej oblicza się wg następującej formuły:
rfp TFC
BEP = - - -
Uzupełnić str.24
Przykład 2. Ocena wrażliwości projektu inwestycyjnego na zmiany stopy dyskontowej i czasu życia projektu
24
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej
WSB
W strategii inwestowania firmy przewiduje się montaż nowych maszyn i urządzeń, których cena zakupu wynosi 12 tyś. PLN. Spodziewany czas ich eksploatacji t=8 lat. Oszacowana stopa dyskontowa = 10%, a uzyskana roczna nadwyżka finansowa w okresie eksploatacji maszyn i urządzeń będzie wynosiła 5 tyś. PLN. Inwestor oczekuje, że po okresie eksploatacji wartość likwidacyjna będzie kształtowała się na poziomie 2 tyś. PLN.
Należy przeprowadzić analizę wrażliwości projektu do wariantu bazowego inwestycji, przy uwzględnieniu zmian stopy dyskontowej i czasu eksploatacji inwestycji.
Ze względu na jednakowe roczne saldo przepływów należy zastosować współczynnik dyskontowania równych płatności rocznych (annuitowy), czyli
. Zdyskontowana wartość netto NPV przy t = 8 i r = 10% wynosi:
NPVB =-12 + 5[
0,1(1+ 0,1)
-] + 2(1 + 0,1)-8 = -12 + 5 * 5,335 + 2 * 0,466 = 15.607
W rachunku wrażliwości scenariusz zmian stopy dyskontowej dla wariantów:
X (r = 9%) NPVX = -12 + 5 * 5,535 + 2 * 0,502 = 16,679
Y (r - 11%) NPVY = - 12 + 5 * 5,146 +2 * 0,434 - 14,598.
Przy okresie wydłużonego czasu użytkowania inwestycji (t = 11 lat) wartość NPV dla trzech analizowanych scenariuszy wyniesie:
NPVB = - 12 + 5 * 6,495 + 2 * 0,350 - 21, 175 NPVX= - 12 + 5 * 6,805 + 2 * 0,387 = 22,799 NPVY = - 12 + 5*6,206 + 2*0,317 = 19,664
Macierz wrażliwości projektu inwestycyjnego na zmiany stopy dyskontowej i czasu życia
inwestycji (w tyś. PLN)
Czas życia inwestycj i (lata) |
Wartość NPV przy stopie dyskontowej |
||
|
9% 10% 11% |
||
t = 5 |
NPVX = 8,7 |
NPVB = 8,2 |
NPVY = 7,7 |
tB = 8 |
NPVX=16,7 |
NPVB=15,6 |
NPVY= 14,6 |
t= 11 |
NPVX = 22,8 |
NPVB = 21,2 |
NPVY= 19,7 |
Zastosowanie analizy wrażliwości nie znajduje uzasadnienia, gdy stopień niepewności zmiennych jest zbyt duży lub istnieje duża współzależność zmiennych. Wówczas należy
25
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
wykorzystywać probabilistyczne - statystyczne i symulacyjne metody pomiaru ryzyka inwestycyjnego lub strategię gier.
Metody probabilistyczne - statystyczne w pomiarze ryzyka
l. Założenia wyjściowe i zasady zastosowania metod Założenia wyjściowe:
horyzontu czasowego (t) budowy i eksploatacji,
kryterium oceny efektywności projektu inwestycyjnego np. NPV,
definicji rozłącznych pojęć mających istotne znaczenie z punktu widzenia
mechanizmów zastosowania metod, np. rzeczywiście osiągnięta NPV i
oczekiwana NPV (spodziewana w przyszłości), oszacowana NPV, możliwe
salda przepływów w przyszłości z różnymi prawdopodobieństwami. Salda
przepływów pieniężnych to zmienne losowe w danym horyzoncie czasu
realizacji i eksploatacji inwestycji; te salda to różnice między przychodami
i kosztami (ujemne w okresie budowy i dodatnie w czasie eksploatacji).warunki realizacji projektu, głównie związanych z charakterystyką zdarzeń
inwestycyjnych (zmiennych losowych) w czasie, np. sald przepływów
środków pieniężnych.wariantów i scenariuszy projektów inwestycyjnych uwzględniających
wszystkie skrajnie możliwe niepewne warunki inwestowania (korzystne i
niekorzystne).
Metody te są związane z rachunkiem ustalania wartości oczekiwanych i ze statystycznym pomiarem ryzyka. Zakłada się, że istnieje rozkład prawdopodobieństw kształtowania się zmiennych rachunku efektywności inwestycji na określonym oczekiwanym poziomie.
Można wyróżnić podstawowe zasady zastosowania metod probabilistyczne -statystycznych w pomiarze ryzyka:
Gdy salda przepływów środków pieniężnych w okresie realizacji projektu
są zmiennymi losowymi, to kryterium oceny efektywności ekonomicznej
tego projektu stanowi oczekiwana wartość zaktualizowana netto NPV, a nie
wartość zaktualizowana netto.Strumienie sald przepływów środków pieniężnych związanych z danym
projektem inwestycyjnym mogą być niezależne lub zależne w czasie:
gdy w kolejnych okresach (latach) salda są niezależne, to wariancja wartości
zaktualizowanej netto zdeterminowana jest tylko wariancją sald w
poszczególnych okresach przy danej stopie dyskontowej, a więc stanowi ich
sumę;gdy w kolejnych okresach salda są zależne (tzn. prawdopodobieństwa ich
wystąpienia są uwarunkowane uprzednio realizowanymi saldami), to przy
obliczaniu wariancji wartości zaktualizowanej netto niezbędne jest
uwzględnienie kowariancji sald w czasie; obliczanie tych kowariancji zatem
występuje przy założeniu, że zyski i straty generowane w realizacji są zależne.
W rezultacie dobór i wykorzystanie tych metod zależy od tego, czy:
26
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
salda przepływów pieniężnych osiągane w poszczególnych latach są
niezależne, czyli saldo uzyskane w roku t nie ma wpływu na poziom
sald uzyskanych w następnym roku (t+1) => wówczas oblicza się
wariancję i odchylenie standardowe tych sald —> nadrzędny scenariusz
o bardzo dobrych tendencjach rozwoju w gospodarce;saldo przepływów pieniężnych w danym czasie t jest zależne od salda
uzyskanego w poprzednim okresie (t-1) i występują
prawdopodobieństwa warunkowe :=> wówczas oblicza się kowariancję
sald -> nadrzędny scenariusz o dobrych tendencjach makro i
mezogospodarczych.
W skomplikowanych sytuacjach decyzyjnych rozłożonych w czasie wykorzystywana jest metoda decyzyjnego drzewa inwestycyjnego.
2. Pomiar ryzyka w warunkach niezależności zmiennych w czasie Wariancyjne ryzyko inwestycyjne
W ujęciu porobabilistycznym ocena ryzyka inwestycyjnego polega na oszacowaniu kilku możliwych poziomów sald przepływów środków pieniężnych dla każdego okresu i określenia prawdopodobieństw ich wystąpienia w celu ustalenia oczekiwanego salda tych przepływów. Następnie dokonuje się pomiaru ryzyka, zakładając, że standardowymi jego miarami są statystyczne miary rozproszenia, a więc wariancja, odchylenie standardowe i współczynnik zmienności.
Etap I
Oczekiwaną wartość salda niezależnych przepływów pieniężnych dla każdego okresu
oblicza się wg wzoru: E(St) = poprawic srt27
gdzie: i = l,2,..mt - numery prawdopodobnych poziomów przepływów pieniężnych w okresie t; symbol mt oznacza, że liczba tych przepływów może być zróżnicowana w poszczególnych latach budowy i eksploatacji;
Stj - saldo przepływów pieniężnych w okresie t na poziomie i;
Pti - wskaźnik prawdopodobieństwa kształtowania się przepływów pieniężnych w okresie t na poziomie i, przy spełnieniu warunku Eptj = l.
Możliwe salda Stj są traktowane jako zmienne losowe. Natomiast oczekiwana wartość E(St), wiążąca się z niepewnością, jest określana jako średnia ważona możliwych do zrealizowania sald przepływów pieniężnych w wagami równymi prawdopodobieństwom ich realizacji.
Po oszacowaniu wartości prawdopodobnej wszystkich sald przepływów pieniężnych należy obliczyć oczekiwaną wartość zaktualizowaną netto:
E(NPV) = ^ [str27 popraw] E(S, )a, gdzie: at - współczynnik dyskontujący dla okresu t, tj.
—. Dla uproszczenia zakłada się, że nakład
początkowy występujący w okresie t = O jest pewny, tj p = l. Gdyby go uwzględnić, to
poprawic poprawic wzory str28
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
wzoru:
E(NPV) = -S„
Etap II
Obliczanie wariancji sald przepływów pieniężnych V(St) dla każdego okresu t wg
m,
V(St)-2^[S,l-E(Siy\2pll. Następnie oblicza się wariancję
zaktualizowanych sald przepływów, czyli wariancję wartości bieżącej wartości netto V(NPV):
n
V(NPV) = VF(5,)a, . Wariancja wartości NPV jest średnią ważoną kwadratów
(=0
odchyleń możliwych do zrealizowania sald od oczekiwanej zaktualizowanej wartości salda przepływów pieniężnych E(NPV). Wariancja wartości NPV jest wyrażona jest w procentach podniesionych do kwadratu. W praktyce korzystniejsze jest operowanie pierwiastkiem z wariancji, czyli odchyleniem standardowym.
Etap III
Ustalenie odchylenia standardowego NPV: 5(NPV} = ^V(NPV) =
Podobnie jak wyżej wartość zero przyjmuje w sytuacji braku ryzyka odnośnie do przyszłego poziomu salda przepływów pieniężnych.
Etap IV
Ustalenie współczynnika zmienności wartości zaktualizowanej netto NPV:
8(NPV)
C(NPV) = — . Współczynnik może przyjąć wartości z przedziału (- co, + oo),
.C* l J V j( V J
czyli nie jest mianowany. Wielkość ryzyka na jednostkę oczekiwanej wartości NPV powinna być najmniejsza.
Ponieważ odchylenie standardowe informuje, o ile przeciętnie przyszła wartość zaktualizowana netto NPV ocenianego projektu może odchylać się (plus, minus) od obliczonej oczekiwanej wartości E(NPV). Wraz z współczynnikiem zmienności oznacza, że prostym kryterium oceny projektu inwestycyjnego jest minimalizacja ryzyka względem oczekiwanej wartości NPV. W praktyce to kryterium jest realizowane przez maksymalizację E(NPV) oraz minimalizację V(NPV) i odchylenia standardowego 8(NPV).
Przy założeniu, że rozkład prawdopodobieństwa jest normalny, rzeczywiste saldo przepływów będzie zawarte w 68,26% przypadków w granicach ± odchylenia standardowego, 95,46% przypadków w granicach ± 2 odchyleń standardowych, a w 99,74% przypadków w granicach ± 3 odchyleń oczekiwanego salda (reguła trzech sigm). Bardziej skomplikowana jest sytuacja, gdy rozkład zmiennej znacznie różni się od rozkładu normalnego.
W inwestowaniu wzrostowi odchylenia standardowego towarzyszy spłaszczenie krzywej dzwonowej. Wynika to z faktu, że wzrost horyzontu czasowego inwestycji jest utożsamiany ze wzrostem trudności weryfikacji warunków inwestowania, a w tym obszaru ryzyka. Krzywe dzwonowe są coraz bardziej spłaszczone dla coraz odleglejszych okresów. Oznacza to tendencje do zmniejszania wartości oczekiwanej i wzrost rozpiętości ryzyka w późniejszych przedziałach czasu.
28
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
Współczynnik zmienności jest przydatny również w procesie oszacowania premii z tytułu ryzyka. Premia za ryzyko to różnica między zyskiem z realizacji projektu inwestycyjnego w warunkach niepewnego otoczenia a zyskiem z inwestycji pozbawionej ryzyka. Premia z tytułu ryzyka może być rozpatrywana jako funkcja współczynnika zmienności, ponieważ jego poziom jest proporcjonalny do ryzyka. Oznacza to, że wraz ze wzrostem tego współczynnika wzrasta ryzyko towarzyszące realizacji projektu inwestycyjnego.
Gdy poziom współczynnika zmienności jest wysoki, należy powtórzyć obliczanie oczekiwanej wartości NPV przy uwzględnieniu stopy procentowej zwiększonej o premię z tytułu ryzyka, w celu wzrostu granicznej stopy rentowności. W takim wariancie uzyskana kolejna dodatnia wartość NPV jest argumentem przemawiającym za realizacją inwestycji nawet przy dużym ryzyku.
Przykład 3 Weryfikacja mierników pomiaru ryzyka dla kilku różnych projektów inwestycyjnych
Istnieją 4 warianty strategii inwestowania w postaci projektów A,B, C i D. Możliwe wartości zdyskontowane netto NPV tych projektów są zdeterminowane pięcioma możliwymi tendencjami do zmian makrogospodarczych i mezogospodarczych w otoczeniu projektów z odpowiednimi prawdopodobieństwami (5 scenariuszy).
Należy ustalić, który projekt inwestycyjny powinien być realizowany wg kryterium maksymalizacji oczekiwanej wartości bieżącej netto E(NPV).
Wartości zaktualizowane netto NPV oraz prawdopodobieństwa ich wystąpienia dla
projektów A, B. C i D
Tendencje gospodarcze |
prawdopod obieństwo |
Projekt A NPVA |
Projekt B NPVB |
Projekt C NPVC |
Projekt D NPVD |
bardzo dobra |
0,1 |
200 |
100 |
250 |
210 |
Dobra |
0,2 |
110 |
55 |
140 |
150 |
przeciętna |
0,3 |
25 |
25 |
30 |
50 |
trudności |
0,3 |
-20 |
15 |
-40 |
-60 |
Zła |
0,1 |
-100 |
-50 |
-165 |
-200 |
W pierwszym etapie należy porównać projekt A i B.
E(NPV)A = 0,1*200 + 0,2*110 + 0,3*25 + 0,3*(-20) + 0,1*(-100) =
= 20 + 22 + 7,5 +(-6) + (-10) = 33,5
E(NPV)B = 0,1*100 + 0,2*55 + 0,3*25 + 0,3*15 + 0,1*(-50) =
= 10+ 11+7,5+ 4,5+ (-5) = 28
E(NPV)A > E(NPV)B , zatem inwestor powinien preferować wariant A, ale wariant B może spowodować mniejsze ujemne salda w warunkach recesji, więc przy awersji do ryzyka może zdecydować się na wariant B, niezależnie od oczekiwanej NPV.
Miarą ryzyka jest wariancja V(NPV) i odchylenie standardowe 8(NPV) wg
formuły:[popraw str29 ] 5(NPV) = [ZPi * (NPVj - E(NPV))2]0'5
29
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej
WSB
Dla projektu A wariancja V(NPV)A = 6605,23 Dla wariantu B wariancja V(NPV)B = 1326,00
=81,27
S(NPV)A =
8(NPV)B = ^1326,00 = 36,41
Poziom odchylenia standardowego informuje o średnim odchyleniu możliwych do osiągnięcia wartości NPV od oczekiwanej wartości NPV. Pod tym względem ryzyko towarzyszące A jest większe od ryzyka projektu B.
Zakłada się, że projekty C i D charakteryzują się odpowiednio tą samą oczekiwaną
wartością bieżącą co A i B, tj. E(NPV)C = 33,5 i E(NPV)D = 28.
Dla projektu C Dla projektu D
V(NPV)C= 12520,23 V(NPV)D= 13956
Natomiast wariancja i odchylenie standardowe wynosi:
5= 712520,23=111,89 §= Vl3956=118,13.
Z rozważanych projektów A i C, charakteryzujących się największą oczekiwaną wartością E(NPV), ale na takim samym poziomie należy wybrać A (najmniejsze ryzyko). Spośród B i D należy wybrać B o znacznie mniejszym ryzyku.
W pierwszym etapie analizy decydent jednoznacznie powinien odrzucić wariant D.
8(NPV) Współczynnik zmienności C(NPV) = „,„„„, wynosi:
Dla projektu A Dla projektu B Dla projektu C Dla projektu D
E(NPV)
81,3 : 33,5 = 2,42 36,4:28-1,3 111,9:33,5 = 3,34 118,1 : 28,0 = 4,22
Zestawienie oczekiwanej NPV, odchylenia standardowego i współczynnika zmienności dla projektów A, B, C i D
Mierniki oceny ryzyka projektu |
Projekty inwestycyjne A B C D |
|||
Oczekiwana wartość NPV |
33,5 |
28,0 |
33,5 |
28,0 |
Odchylenie standardowe |
81,3 |
36,4 |
111,9 |
118,1 |
Współczynnik zmienności |
2,4 |
1,3 |
3,3 |
4,2 |
Spośród najkorzystniejszych A i B inwestor charakteryzujący się niechęcią do ryzyka wybierze projekt B, ponieważ tylko 1,3 jednostek ryzyka przypada na jednostkę oczekiwanej wartości NPV. Natomiast inwestor preferujący ryzyko zdecyduje się na realizację projektu A mając na uwadze również oczekiwaną wartość E(NPV).
3. Metoda drzewa decyzyjnego
Metoda decyzyjnego drzewa inwestycyjnego umożliwia graficzną interpretację złożonych strumieni sald przepływów pieniężnych (zysków i strat) oraz prawdopodobieństw ich wystąpienia. W definicji drzewa:
> pień drzewa jest utożsamiany z wyjściowym problemem decyzyjnym, np.
może to być decyzja dotycząca celu i wielkości nakładu początkowego
związanego z uruchamianiem projektu;
30
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
> konary i rozgałęzienia pnia drzewa są utożsamiane z jednej strony z możliwościami występowania i wyboru różnych zdarzeń inwestycyjnych, a z drugiej strony z możliwościami wystąpienia efektów różnych wyborów przedsięwzięć inwestycyjnych zdeterminowanych tymi różnymi zdarzeniami.
W rezultacie z jednej strony rozgałęzieniem danego konara jest splot decyzyjny, z drugiej zaś - rozgałęzieniem danego konara jest splot wyników, który w przyszłości będzie wyznacznikiem kolejnych splotów (przyczyna -> skutek —> przyczyna). W tej metodzie istotne znaczenie maj ą następując e relacje:
Założenia projektu inwestycyjnego i początkowy nakład inwestycyjny —» możliwe zdarzenia inwestycyjne —> splot decyzyjny —> możliwe efekty zdarzeń inwestycyjnych -> splot wyników głównie ekonomicznych —> oczekiwane końcowe efekty wyborów przedsięwzięć inwestycyjnych.
W związku z tym drzewa decyzyjne są • wykorzystywane głównie wtedy, gdy występują warunkowe prawdopodobieństwa zdarzeń i warunkowe decyzje inwestycyjne. Są to bieżące decyzje podejmowane w pewnej kolejności i w konkretnym czasie. Dzięki tej analizie inwestor może sprawnie i efektywnie na bieżąco oceniać projekt w celu podjęcia decyzji o wzroście wydatków w zamian za dodatkowe wpływy, albo może on przerwać realizację tego projektu. Co więcej, drzewo decyzyjne umożliwia także dokonanie wielokrotnej analizy wrażliwości oraz zmodyfikowanie podstawowych parametrów i założeń, a także zbadanie wpływu tych zmian na zalecany kierunek przyszłych działań.
Ryzyko obliczone tą metoda powinno być kompensacją niepewności osiągnięcia celu i założeń (techniczno - organizacyjnych, prawno - ekonomicznych) projektu inwestycyjnego oraz całego jego dynamicznego otoczenia.
Przykład 4. Problem poszukiwań ropy: wiercić czy nie wiercić?
Poszukiwacz ropy musi zdecydować, czy rozpocząć wiercenie szybu naftowego w pewnym miejscu przed wygaśnięciem zezwolenia na odwierty. Koszt wiercenia wynosi $200tys. Suma ta zostanie stracona (koszt utopiony), jeśli odwiert okaże się ,,suchy". W przeciwnym razie - według ocen poszukiwacza - całkowite przychody z eksploatacji szybu naftowego wyniosą SSOOtys. Prawdopodobieństwo wystąpienia złóż ropy (na podstawie wyników badań geologicznych) wynosi 0,4 (szansa znalezienia ropy wynosi 40%). Zatem prawdopodobieńst\vo niepowodzenia wynosi 0,6. Kryterium podejmowani decyzji jest wartość oczekiwana, ponieważ pozwala ono menedżerowi wybór wariantu działania, pozwalający zmaksymalizować wielkość oczekiwanego zysku.
Posuwając się po drzewie decyzyjnym z lewa w prawo można prześledzić sekwencję zdarzeń składających się na proces decyzyjny. Początkiem sekwencji jest węzeł decyzyjny, oznaczony zwykle kwadratem. Wychodzą z niego dwie możliwe do podjęcia decyzje. Jeśli decyzja o podjęciu poszukiwań jest pozytywna, to w schemacie drzewa pojawia się kółko. Zdarzenie losowe jest sposobem wyrażenia ryzyka związanego z podjęciem wierceń. Opis dopełnić trzeba prawdopodobieństwem wystąpienia złoża ropy (p = 0,4). Wariant „nie wiercić" jest pewny i daje wynik $0 (podwójna linia oznacza odrzucenie wariantu). Oczekiwany wynik (zysk) w wariancie „wiercić" wynosi: WO = 0,4* 600 tyś. + 0,6(-200 tys.)= 120 tyś.
Im większe prawdopodobieństwo określonego wyniku, tym większy jego wpływ na wartość oczekiwaną zysku (tym bardziej zbliża się on do tej wartości).
31
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
mokro 600
0,4
wiercić
x-—V
0,6
wiercić
nie wiercić O
-200
Gdy decyzja jest bardziej złożona, to wartość oczekiwaną oblicza się etapami, dokonując „wstecznego uśrednienia" wyników otrzymanych na końcu poszczególnych gałęzi.
Metody symulacyjne
Metody te należą do najbardziej skutecznych narzędzi stosowanych przez podejmujących decyzje w warunkach niepewności i ryzyka. W przypadku projektów inwestycyjnych stosowanie symulacji uzasadnia w szczególności fakt, że projekty te podlegają równoczesnemu oddziaływaniu wielu zróżnicowanych czynników obciążonych ryzykiem.
Badania symulacyjne (najbardziej znane jako metoda Monte Carlo) polegają na konstruowaniu modeli, opisujących matematycznie strukturę i funkcjonowanie występującego w rzeczywistości badanego systemu, np. przedsiębiorstwa lub projektu inwestycyjnego i następnie na odtwarzaniu za pomocą tych modeli kolejnych stanów analizowanego systemu w celu określenia jego właściwości. Inaczej mówiąc, przy decyzjach inwestycyjnych jest to wielokrotne powtarzanie procedury obliczania wartości miary efektywności projektu zgodnie z modelem dla generowanych losowo wartości zmiennych niepewnych wpływających na tę wartość. W modelach symulacyjnych określa się powiązania wszystkich zmiennych, które mogą wystąpić z mniejszym lub większym prawdopodobieństwem i ustala się wszystkie możliwe wyniki.
W procesie symulacji stosuje się na ogół dwa podejścia; w pierwszym wykorzystuje się metody teorii gier, w drugim stosowany jest proces powtarzalnego eksperymentowania. W ramach teorii gier symulacja odzwierciedla przeciwstawne interesy uczestników gry w symulowanym środowisku. Symulację stosująca powtarzalne eksperymentowanie można podzielić na dwa rodzaje:
opartą na deterministycznych modelach symulacyjnych, w których
zakłada się, że zmienne modelu przyjmują określone wartości. Za
pomocą tych modeli uzyskuje się odpowiedź na pytanie „co będzie,
jeśli?";opartą na probabilistycznych (stochastycznych) modelach. W tego
typu modelach zmienne mogą być przyjmowane jako znane z
pewnością (traktowane jako stałe) lub są reprezentowane za pomocą
ich rozkładów prawdopodobieństwa (zmienne losowe będące poza
kontrolą podejmującego decyzje).
Analiza symulacyjna nie jest metodą eliminowania ryzyka. Jej wyniki nie są wiążące, ale są źródłem ważnych informacji, istotnie wspomagających proces decyzyjny zorientowany na wzrost atrakcyjności ekonomicznej projektu. Im większa różnorodność i siła wrażliwości projektu na zmiany, tym większe ryzyko i potrzeba zastosowania metod symulacyjnych.
32
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej
WSB
Bardziej złożona decyzja dotycząca wierceń
$26
$26
5000 baryłę 0,15
ropa na B
głębokości 900 m
8000 baryłek
16 000 baryłek
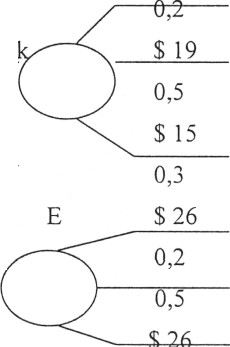
0,13
0,55
0,3
D
0,3
5000 baryłek
ropa na głębokości 1500 m
0,24
0,21
brak ropy 0,66
-400
33
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej
WSB
Metody operacyjne - strategia gier
Metody te służą do rozwiązywania konkretnych sytuacji decyzyjnych w celu wyznaczenia decyzji optymalnych i są wykorzystywane, gdy istnieje konieczność koordynacji dużej liczby czynników zmierzających do osiągnięcia określonego celu, przy założeniu optymalnego układu tych czynników. Strategia gier umożliwia stosunkowo dokładne poznanie skutków poszczególnych wariantów decyzji inwestycyjnych. Decyzje są podejmowane w warunkach pewności, niepewności (nie mogą być opisane ani modelem deterministycznym ani probabilistycznym) i ryzyka. Z punktu widzenia analizy strategicznej wyróżnia się cztery grupy czynników efektywności inwestowania (analiza SWOT).
Macierz decyzyjna w analizie SWOT przy uwzględnieniu kombinacji czynników
niepewnych
Stan otoczenia |
|
STRATEGIE |
|
|
|
Czynniki pewne Wewnętrzne Pw |
Czynniki niepewne Wewnętrzne Nw |
|
Czynniki pewne Zewnętrzne Pz |
Pz <-»Pw maxi - maxi |
pz<-»nw maxi - mini |
|
Czynniki niepewne zewnętrzne Nz |
N2 <-»Pw mini - maxi |
N2«-»NW mini - mini |
P2 <-»Pw Inwestor jest w najkorzystniejszej sytuacji, ponieważ otoczenie
stwarza szansę. Należy maksymalizować stopień wykorzystania tych
atutów.Nz <-» Nw Inwestor jest w najgorszej sytuacji, ponieważ zagrożenia
zewnętrzne są wzmacniane przez słabości wewnętrzne przedsiębiorstwa
realizującego projekt inwestycyjny. Należy minimalizować te słabości.
Strategia w wersji pesymistycznej prowadzi do zaniechania projektu, a w
wersji optymistycznej do przeczekania sytuacji.P z <-» Nw Szansę zewnętrzne są trudne do wykorzystania, ponieważ istnieją
słabości samego projektu inwestycyjnego. Zastosowana strategia maxi-minu
powinna być ukierunkowana na minimalizację słabości w celu
wykorzystania szans zewnętrznych.Nz <->Pw Atuty projektu, sprzyjające poprawie pozycji decydenta są
narażone na zewnętrzne zagrożenia. Inwestor poprzez zastosowanie strategii
mini - maxu powinien przeciwstawić się trudnościom, jakie stwarza
otoczenie w celu wykorzystania swojego potencjału wewnętrznego do
maksimum.
W literaturze proponuje się szereg kryteriów podejmowania decyzji, spośród których do najważniejszych należą:
* kryteria maksymalizujące bezpieczeństwo, tj. rozpatrujące jedynie najgorsze konsekwencje podejmowania decyzji:
34
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
kryterium wypłaty maximin Wałda wynika z zasady pesymistycznej i polega na wyborze
minimalnej wypłaty (największej straty) z każdej strategii, a następnie wyborze wariantu o
najwyższej minimalnej wypłacie lub alternatywnie na wyborze strategii o najmniejszej
maksymalnej stracie, czyli zabezpiecza najwyższy minimalny poziom wypłaty
(najmniejszy maksymalny poziom straty);kryterium żalu minimax Savage'a wyprowadzone z najmniejszej maksymalnej straty,
doty
czy odjęcia bieżącej wypłaty od potencjalnej, tj. sumy, która mogłaby być uzyskana,
gdyby stan natury był znany w chwili podejmowania decyzji. Ta różnica jest „żalem"; w
każdej strategii należy zaznaczyć największą różnicę, a spośród nich wybrać wariant o
najniższej wartości (wybiera się wariant o najmniejszym maksymalnie możliwym
rozczarowaniu, które wynika z różnicy między wynikiem maksymalnie możliwym do
uzyskania a wynikami możliwymi do uzyskania przez każdy z pozostałych wariantów).
Jest więc to kryterium gwarantujące najmniejszy maksymalny żal;kryteria decyzji oparte jednocześnie na najlepszych i najgorszych wynikach:
kryterium indeksu pesymizmu Hurwicza tworzone jest poprzez nadanie rezultatom
odpowiednich wag nawiązujących do stopnia pesymizmu decydenta zgodnie z
następującymi regułami:
1. wprowadzeniem stałej wielkości 0<a<l, odzwierciedlającej „indeks
pesymizmu" decydenta;
2. wybraniem z każdej strategii działania / (/=7,2,...) minimalnej m, i maksymalnej
wypłaty A//;
3. obliczeniem a-indeksu dla każdej strategii według formuły am,+(l-a)Mi, który interpretuje się jako średnią ważoną z najniższej i najwyższej wypłaty, skorygowaną przez współczynnik pesymizmu a i (1-a). Najmniej ryzykowną decyzją jest strategia o najwyższym a-indeksie;
Kryterium masymaksu związane z optymistyczną zasadą Hurwicza polega na wyborze wariantu, którego wynik (skutek) jest najbardziej wartościowy w sytuacji najbardziej sprzyjającej.
* zasada niewystarczającej przyczyny Łapiące 'a i Bayesa wywodzi się z twierdzenia, że
decydent w warunkach „całkowitej ignorancji" powinien założyć, iż wystąpienie
wszystkich możliwych stanów natury jest jednakowo prawdopodobne
(prawdopodobieństwa są równe, gdy nie są znane). Regułą postępowania jest
przemnożenie prawdopodobieństwa wystąpienia danego stanu natury przez poziom
wypłat w każdej strategii w celu otrzymania oczekiwanej użyteczności z danej strategii i
wybór strategii z najwyższą wypłatą.
W procesie podejmowania decyzji inwestycyjnych w warunkach niepewności z orientacją na najgorsze możliwości spośród wymienionych kryteriów, zastosowanie ma kryterium pesymistyczne (maksyminu) i kryterium rozczarowania (minimaksu).
Sposób postępowania przy zastosowaniu zasad i metod strategii gier:
Obliczanie wskaźników efektywności dla wszystkich analizowanych
wariantów decyzji inwestycyjnych. Wariantom można przypisać
scenariusze decyzyjne różniące się wszystkimi możliwymi
kombinacjami czynników niepewnych;Każdy wariant decyzji inwestycyjnych (Wi. ...Wn) ma dwa lub
więcej scenariuszy, np. wariant Wj ma scenariusze Sei, ...Sem-
35
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej
WSB
Przyjmuje się a priori, że trudno jest jednoznacznie ustalić, które ze
scenariuszy decyzyjnych sensu stricto są optymistyczne lub
pesymistyczne, ponieważ dany scenariusz może być optymistyczny
w świetle danego wariantu , a w świetle innego - pesymistyczny.Opracowanie decyzji inwestycyjnej według formuły maksyminu i
minimaksu.
Opracowanie decyzji wg maksyminu
Należy wybrać dla każdego wariantu takiego scenariusza, który charakteryzuje się najgorszymi wskaźnikami, następnie wybrać wariant z najwyższym poziomem spośród tych najniższych wskaźników efektywności.
Projekt inwestycyjny |
Możliwe wskaźniki efektwności Sel Se2 . Se3 |
Minimalny poziom wskaźnika \v danym wariancie |
||
W, |
1,0 |
1,7 |
1,1 |
1,0 |
W2 |
1,2 |
1,1 |
1,4 |
1,1 |
W3 |
1,3 |
1,5 |
1.6 |
1,3 |
Opracowanie decyzji wg formuły minimaksu dotyczy wyboru wariantu najlepszego z każdego scenariusza, a następnie obliczeniu różnicy między wskaźnikiem efektywności tego najlepszego i wskaźnikami efektywności dla poszczególnych scenariuszy. W trzecim etapie dla każdego wariantu jest wybierany taki scenariusz, który charakteryzuje się największą różnicą efektywności ze wszystkich obliczonych różnic. Ostatecznie, wybierany jest wariant, który w razie faktycznej realizacji niewłaściwego scenariusza spowoduje minimalną stratę w porównaniu do wariantu, jaki byłby najkorzystniejszy przy tym scenariuszu.
Projekt inwestycyjny |
Możliwe różnice wskaźników efektywności jako skutki decyzji |
Max poziom różnicy wskaźników w danym wariancie |
||
|
A Sel A Se2 A Se3 |
|
||
W, |
0,3 |
0,0 |
0,5 |
0,5 |
W2 |
0,1 |
0,6 |
0,2 |
0,6 |
W3 |
0,0 |
0,2 |
0,0 |
0,2 |
W tym wypadku istnieją podstawy do podjęcia decyzji realizacji projektu W3 przy minimaks = 0,2. Zastosowanie formuły minimaksu zobowiązuje do podjęcia decyzji, która zapewnia najmniejszą stratę spośród największych strat mogących wystąpić w niepewnych warunkach realizacji przedsięwzięcia inwestycyjnego. Najczęściej może dotyczyć inwestycji prestiżowych lub ekologicznych, które znaj duj ą uzasadnienie społeczne.
Konwencjonalne podejmowanie ryzyka w procesie decyzyjnym dotyczącym inwestycji w infrastrukturę opiera się na założeniach, że efekty działań można zdefiniować i skonkretyzować oraz że istnieje możliwość określenia i pomiaru ekonomicznych efektów każdego wariantu. Poszerzenie analizy o efekty środowiskowe wprowadza dodatkowy element niepewności. Ponadto zrealizowanie przewidywanych korzyści może nie być
36
prrT. T:resa Kurnińska: Rrcrko ir dzLihtlr.ośc: '^osnodarczei V\'S;;
spełnione ze względu na brak możliwości określenia prawdopodobieństwa wystąpienia skali i charakteru zagrożeń środowiskowych. Stosuje się wówczas analizę dopuszczalnego ryzyka lub/i analizę decyzji.
Tą pierwszą wykorzystuje się, gdy nie ma jednoznacznie określonych metod wyboru stosowanych przy poszukiwaniu najbardziej akceptowanego wariantu (analiza uzupełniona jest opiniami ekspertów i ludzi reprezentujących różne grupy społeczne oraz doświadczeniami z przeszłości).
Ta druga bada, w jaki sposób uświadomienie sobie ryzyka wpływa na podejmujących decyzje18, ponieważ tradycyjna metoda kosztów-korzyści zakłada neutralność ryzyka.
Gdy celem jest zapobieganie wydarzeniom niosącym realne zagrożenia, to powinno się stosować analizę ryzyka i korzyści, która jest odwróceniem analizy kosztów-korzyści, gdyż opiera się na założeniu, że zamierzenie nie zostanie podjęte. Z drugiej strony korzyści wynikające z bezczynności równe są oszczędnościom wynikającym z zaniechania stosowania zabezpieczeń. Jeżeli koszty niepodjęcia inwestycji są mniejsze od korzyści zaniechanie inwestycji jest usprawiedliwione i odwrotnie.
Metodą łączącą założenia analizy decyzji i analizy ryzyka i korzyści jest analiza komparatywnego ryzyka. Warto jej poświęcić więcej uwagi ze względu na to, że jest procesem, w trakcie którego formułowane są narzędzia porównujące znaczenie różnych problemów środowiskowych oraz dostarczające prawodawcom i decydentom bieżących technicznych informacji służących bardziej efektywnemu wyborowi. Typowa analiza komparatywnego ryzyka obejmuje następujące etapy: zdefiniowanie zagrożeń środowiskowych, które muszą być w danym przypadku poddane osądowi, sklasyfikowanie ich według rozmiaru zagrożenia, dokonanie selekcji priorytetów wymagających szczególnej uwagi, ustalenie celów w zakresie obniżenia ryzyka, propozycja strategii porównawczych umożliwiających osiągnięcie zakładanych celów, wdrożenie najbardziej obiecujących strategii, monitorowanie rezultatów i odpowiedniego przystosowania polityki i budżetu w tym zakresie. Na każdym etapie analizy wyszczególniane są typowe problemy według ich rangi, kryteria wyboru i plan działania. Główną zaletą tej analizy jest precyzyjne stawianie problemów ryzyka towarzyszącego podejmowaniu decyzji, następnie zaangażowanie ekspertów i polityków do twórczego przeciwdziałania jemu zarówno w ramach ekspansywnej, jak i restrykcyjnej polityki budżetowej. Wadą jest zbyt dużo posunięć nie gwarantujących zadowalających rezultatów w warunkach niepewności, ponieważ do ryzyka środowiskowego odnoszą się te same ograniczenia wyboru odnośnie do pozostałych zasobów.
Łączenie ryzyka (ubezpieczenie się, różnicowanie portfela inwestycyjnego)
Łączenie ryzyka polega na wykorzystywaniu działania prawa wielkich liczb, zgodnie z którym przeciętny wynik gry jest tym bliższy wartości oczekiwanej, im więcej partii gry zostaje rozegranych. Jeśli zdarzenia są niezależne, a gracze uczciwi, tj. przestrzegają ustalone reguły gry, to wówczas można zawierać formalne umowy, których celem jest zapłata za zmniejszenie ryzyka.
Przypuśćmy, że ktoś ma samochód wart 30 tyś. zł, a prawdopodobieństwo kradzieży w nadchodzącym roku wynosi 0,1. Prawdopodobieństwo, że do kradzieży nie dojdzie, wynosi 0,9. Towarzystwo ubezpieczeniowe oferuje polisę roczną w wysokości 3 tyś. zł. W razie kradzieży ubezpieczyciel wypłaca ubezpieczonemu równowartość 30 tyś. zł. Wykupując polisę, właściciel samochodu rezygnuje z udziału w jednej grze i przystępuje do innej gry. Zanim się ubezpieczył, życie zmuszało go do udziału w grze o wypłatach O zł i - 30 tyś. zł.
18 Decydent nie lubiący ryzyka będzie preferował opcje bez wielkiego ryzyka uzyskania nieoczekiwanego wyniku, czyli unikał rozwiązań mogących przynieść zarówno wielkie korzyści, jak i ogromne straty.
37
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
wypłaty te pojawiały się z prawdopodobieństwem 0,9 i 0,1. W wypadku nowej gry wypłaty wynoszą: - 3 tyś. zł w razie kradzieży (ubezpieczony traci składkę i samochód, lecz odszkodowanie warte tyle samo, co samochód) oraz - 3 tyś. zł, jeśli do kradzieży nie dojdzie (ubezpieczony traci składkę). Prawdopodobieństwo obu zdarzeń nadal równe jest 0,1 i 0,9. Ile wynosi wartość oczekiwana obu gier i jak wysokie jest związane z nimi ryzyko?
Wartość oczekiwana pierwszej gry jest równa:
WOi = - 30 tyś. zł 0,1 + 0*0,9 = - 3tys. + O = - 3 tyś. zł.
WO2 = - 3tys. zł *0,1 + - 3 tyś. *0,9 - - 300 - 2,7 tyś. zł = -3 tyś. zł.
Dla pierwszej gry wariancja wynosi:
= [-30 tyś. zł - (-3 tyś. zł)]2 * 0,1 + (O - 3 tyś. zł)2 * 0,9 =
27
tys.2*0,l + -3tys. 2*0,9 = 72 900 tyś. - 8 100 tyś. = 64 800 tyś. zł.
WG2 = [- 3 tyś. zł - (-3 tyś. zł)]2 * 0,1 + [- 3 tyś. zł - (-3 tyś. zł)]2 * 0,9 = O zł.
= O zł, oznacza, że wynik tej gry nie jest obciążony żadnym ryzykiem.
Zgodnie z definicjami osób z różnymi skłonnościami do ryzyka, osoba niechętna ryzyku, z dwóch gier o takiej samej wartości oczekiwanej, wybierze mniej ryzykowną. Osobom obojętnym wobec ryzyka jest wszystko jedno, czy kupią polisę, czyjej nie wykupią. Natomiast osoby skłonne do ryzyka będą wolały nie ubezpieczać samochodu na opisanych warunkach. Dzięki temu zagrają w grę o takiej samej wartości oczekiwanej jak gra w ubezpieczenie, a w dodatku będą mogły cieszyć się ryzykiem, wynikającym z większej wariancji wyników.
Gra ubezpieczyciela po zawarciu opisanej transakcji wygląda następująco: w razie kradzieży jego wypłata wynosi:
27 tyś. zł = - 30 tyś. zł (odszkodowanie) + 3 tyś. zł (składka ubezpieczającego się).
kiedy do kradzieży nie dochodzi: 3 tyś. zł (składka).
Wypłaty te pojawiają się z prawdopodobieństwem odpowiednio 0,1 i 0,9. Oferując ubezpieczenie, ubezpieczyciel decyduje się na udział w grze o wartości oczekiwanej równej:
WO = - 27 tyś. zł * 0,1 + 3 tyś. zł * 0,9 = - 2,7 tyś. + 2,7 tyś. = O zł.
Wariancja wyników tej gry wynosi:
WG = (-27 tyś. zł - O)2 * 0,1 + (3 tyś. zł - O)2 * 0,9 =
= 72 900 tyś. - 8 100 tyś. = 64 800 tyś. zł. Ubezpieczyciel przejął na siebie całe ryzyko, którego pozbył się ubezpieczający się. Wartość oczekiwana równa się zero, co należy interpretować, że przeciętnie składek ubezpieczających się ledwie starczy na pokrycie wypłacanych odszkodowań. Towarzystwa ubezpieczeniowe znają metody umożliwiające pozbycie się całego ryzyka, które przejęły na siebie19, niekoniecznie powiększając stawki ubezpieczeniowe (co mogłoby sugerować przejęcie ryzyka obciążającego osoby niechętne ryzyku przez tych, którzy lubią ryzykować).
Emisja akcji i sprzedaż na giełdzie to nic innego, jak pozbycie się przez właścicieli przedsiębiorstw części obciążającego ich ryzyka, którego źródłem jest zmienność wyników gospodarowania ich przedsiębiorstw. Ryzyko to zostaje przeniesione na nabywców akcji. To oni poniosą straty spowodowane ewentualnymi niepowodzeniami. Natomiast dochody
' Tu też mamy do czynienia z łączeniem i dzieleniem ryzyka przez różne towarzystwa ubezpieczeniowe.
38
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
właściciela z emisji akcji mogą być przeznaczone na zakup udziałów w innych firmach. W taki sposób właściciele mogą łączyć ryzyko związane z udziałem w różnych grach gospodarczych i w rezultacie obniżać ryzyko swojej działalności Ciągły obrót papierami wartościowymi umożliwia alokację ryzyka na rynku kapitałowym odpowiadającą preferencjom jednostek.
Rynek kapitałowy nie pozwala pozbyć się całego ryzyka związanego z gospodarowaniem. Może się zdarzyć, że w okresie kryzysu gospodarczego prawie wszystkie akcje zaczną przynosić straty, które nie zostaną wyrównane zyskami z innych papierów. W pozostałych fazach cyklu koniunkturalnego można stosować reguły obniżające ryzyko.
Przykład 5. Chcesz zainwestować 10 zł na rynku papierów wartościowych, a w sprzedaży są dostępne akcje banku i fabryki samochodów (obie akcje kosztują po 5 zł). Ich właściciele postanowili rozłożyć ryzyko, jakiemu podlegają na wielu innych inwestorów. Obaj emitenci mogą mieć zarówno rok dobry, jak i zły w swojej działalności. W zależności od rozwoju sytuacji dywidendy i zyski kapitałowe z akcji tych firm zapewnią ich posiadaczom dochód w wysokości, odpowiednio 2 zł lub Izl. Prawdopodobieństwo tego, że nadchodzący rok będzie dobry lub zły, jest równe i wynosi 'h.
Mogłoby się wydawać, że jest obojętne, w jakie akcje zostaną zainwestowane pieniądze. Jednak ważna jest struktura inwestycji. Przy zakupie akcji jednego rodzaju inwestor bierze udział tylko w jednej grze, przy zakupie obu rodzajów akcji, zapewnia udział w dwóch grach i połączenie związanego z nimi ryzyka, co sprawia, że - zgodnie z prawem wielkich liczb - dochód z portfela inwestycyjnego okazuje się bliższy wartości oczekiwanej
gry-
ii
Zakup jednego rodzaju akcji ]] Różnicowanie zakupu akcji
S |
|
BANK |
|
n ii |
BANK |
A M |
|
dobry rok |
zły rok |
u u n n u n |
dobry zły rok rok |
O C |
dobry rok |
4 lub 4 |
41ub- |
n n ii u II II |
2+2=4 2+1=3 |
H O D Y |
zły rok |
-lub 4 |
2 lub 2 |
II II II II II II II II |
1 +2=3 1+1=2 |
Jeśli jest się w posiadaniu tylko akcji banku lub tylko akcji producenta samochodów, to wystąpi tylko albo rok dobry, albo rok zły. Stąd prawdopodobieństwo wystąpienia tych zdarzeń wynosi '/2. Gdy portfel jest zróżnicowany, to mogą wystąpić 4 sytuacje i wówczas prawdopodobieństwo któregokolwiek wynosi '/4.
Chociaż wartość oczekiwana przed i po zróżnicowaniu nie różni się, to ryzyko portfela, mierzone wariancją, po zróżnicowaniu obniża się o 50%.
Przed zróżnicowaniem:
WOi = 4 zł * 0,5 + 2 zł * 0,5 - 2 zł +1 zł = 3 zł
Po zróżnicowaniu:
WO2 = 4zł*0,25 + 3zł*0,25 + 3zł*0,25 + 2 zł*0,25 = 3 zł
39
pro f. Teresa Kamińska: Ryzyko w działalności gospodarczej WSB
Odpowiednio wariancja przed zróżnicowaniem wynosi: WGi= (4zł - 3zł)2 *0,5 + (2zł - 3zł)2 *0,5 = 0,5 zł + 0,5zł = l zł Po zróżnicowaniu:
WG2 = (4zł - 3zł)2 *0,25 + (3zł - 3zl)2 *0,25 + (3zł - 3zł)2 *0,25 + (2zł - 3zł)2 *0,25 = 0,25zł + Ozł + Ozł + 0,25 = 0,5 zł.
Warunkiem powodzenia tej operacji jest niezależność zdarzeń (inaczej nie pojawiłyby się warianty mieszane z dobrym i złym rokiem dla różnych podmiotów).
Należy zwrócić uwagę na inne możliwości analizy ryzyka przy podejmowaniu decyzji inwestycyjnych.
Najczęściej w badaniach ekonomicznych występuje ryzyko związane z aktywami firmy. Wygodnie jest mierzyć ryzyko związane z danym aktywem w relacji do ryzyka rynku kapitałowego jako całości za pomocą tzw. współczynnika p. Współczynnik ten można zapisać jako:
P = (ryzyko akcji i) / (ryzyko całego rynku kapitałowego).
Analiza ryzyka odbywa się za pomocą modelu wykorzystującego współczynnik P, dla każdej z rozważanych inwestycji. Określa się go w wyniku oceny historycznego zapisu dochodowości inwestycji na tle dochodowości rynku, które są badane za pomocą dochodowości akcji wchodzących w skład Indeksu 500 akcji Standard & Poor lub innych indeksów akcji (np. Dow Jones).
Model oceny aktywów kapitałowych umożliwia inwestorowi ustalenie wymaganych zysków od poszczególnych akcji przez zastosowanie następującego równania:
kj = Rf + p j (km - Rf), gdzie: kj - wymagana dochodowość,
Rf- dochodowość aktywu wolnego od ryzyka, Pi - współczynnik P dla aktywu i,
km - średnia dochodowość wszystkich aktywów rynkowych.
Jako dochodowość aktywów wolnych od ryzyka przyjmuje się bieżącą stopę oprocentowania trzymiesięcznych weksli skarbowych. Wyrażenie (k,„ - Rj) nazywane jest rynkową premią ryzyka. Jest to dodatkowy zysk, jaki inwestor musi otrzymać, aby był skłonny zakupić na rynku akcje, a nie wolne od ryzyka papiery rządowe.
Często współczynnik P przyjmuje się dla danego typu aktywów w sposób aprioryczny lub próbuje się go szacować.
Można jednak przyjąć, że ryzyko danego i-tego aktywu zależy od k zmiennych. Zatem ryzyko i-tego aktywu można zapisać jako funkcję wielu zmiennych g(x/, ...,xt<). Inaczej P jest ilorazem dwóch wielowymiarowych (k-wymiarowych) rozkładów. Znając modele różnych rodzajów ryzyk można następnie wykorzystać je do dywersyfikacji ryzyka poprzez zmianę struktury aktywów w danej firmie. Prowadzi to bezpośrednio do dwóch zagadnień teoretycznych i praktycznych, tj. do poszukiwania punktów równowagi oraz do generowania zysków poprzez unikanie ryzyka. Konkludując, subiektywizm bierze się z przyjmowanych założeń apriorycznych o rozkładach i ich parametrach, a także metod szacowania lub stymulowania procesów rzeczywistych, natomiast obiektywizm zawarty jest w fakcie consensusu w środowisku zarządzających finansami, co do powszechnie przyjmowanych założeń o rozkładach w praktycznie stosowanych procedurach i algorytmach decyzyjnych.
40
prof. Teresa Kamińska: Ryzyko w działalności gospodarczej
WSB
Stopa zwrotu to stosunek wyrażonych w pieniądzu korzyści z inwestycji w zakup akcji do wartości zainwestowanej sumy w danym okresie (najczęściej l roku). Portfel rynkowy to wszystkie akcje notowane na giełdzie. Jest zbyt drogi, aby go kupić, jednak prawie każdego stać na odpowiednio mniejszy portfel, którego struktura pokrywa się ze strukturą portfela rynkowego. Oba portfele mają taką samą stopę zwrotu. Dla pewnego przedziału czasu znane są wartości stopy zwrotu z jakiejś akcji oraz stopy zwrotu z portfela rynkowego.
stopa zwrotu z pewnej akcji
* ,.."••*
*,.•••''' * .'••" *
* ...•-' * * ..•••'"*
stopa zwrotu z portfela rynkowego
Linia przerywana to linia najlepszego dopasowania (linia charakterystyczna papieru wartościowego). Ukazuje ona, jakiej stopy zwrotu z inwestycji w akcje konkretnego przedsiębiorstwa można oczekiwać przy danej stopie zwrotu z portfela rynkowego. Linie tę, jak każdą prostą, można opisać za pomocą dwóch parametrów: współczynnika kierunkowego i wyrazu wolnego. Współczynnik kierunkowy to współczynnik (3, który pokazuje siłę reakcji stopy zwrotu z danej akcji na zmiany stopy portfela rynkowego. Załóżmy, że dla akcji X wynosi on 0,67. Oznacza to, że jeżeli stopa zwrotu z portfela rynkowego zmieni się o l punkt procentowy, to stopa zwrotu zmieni się o 0,67 punktu procentowego w tym samym kierunku.
Wyszukiwarka