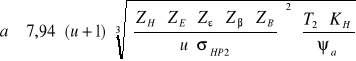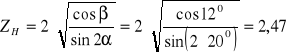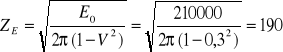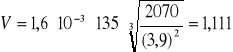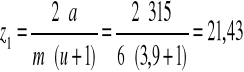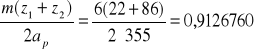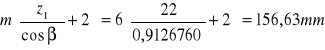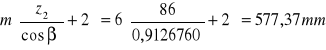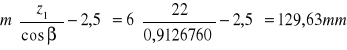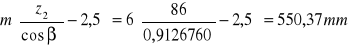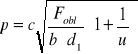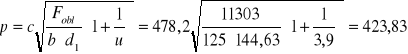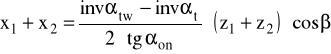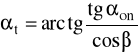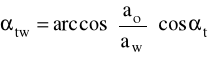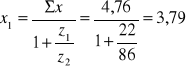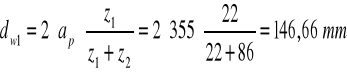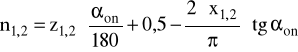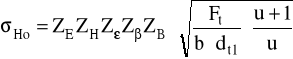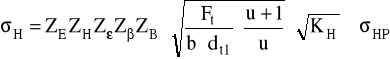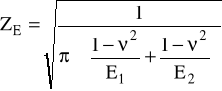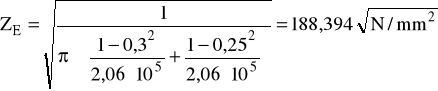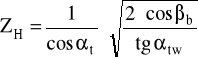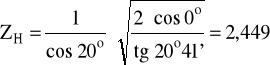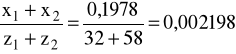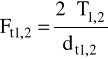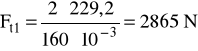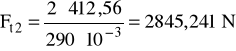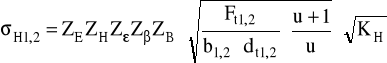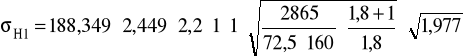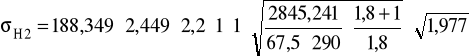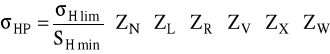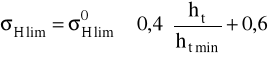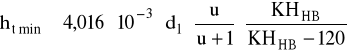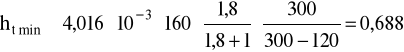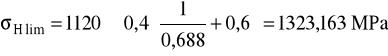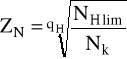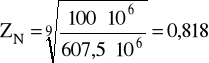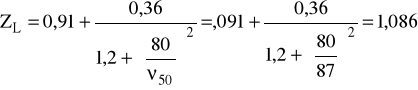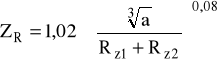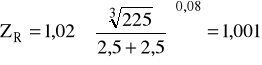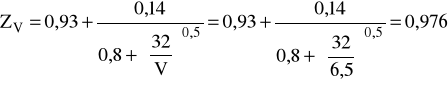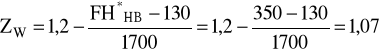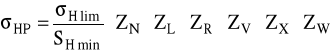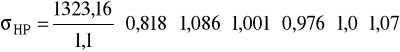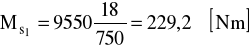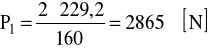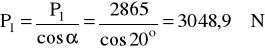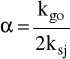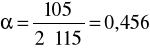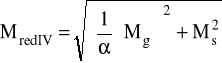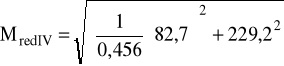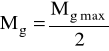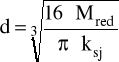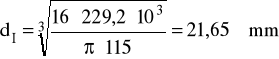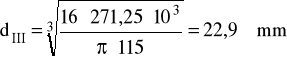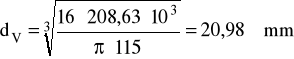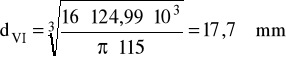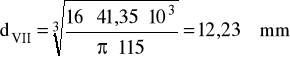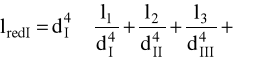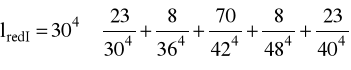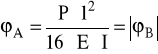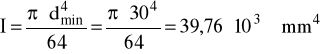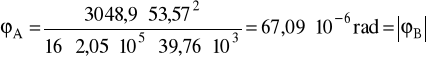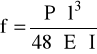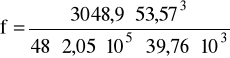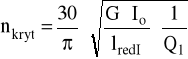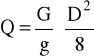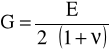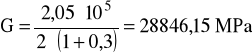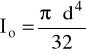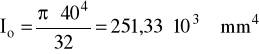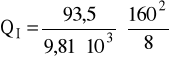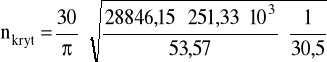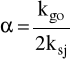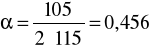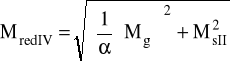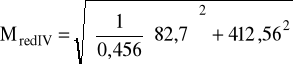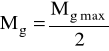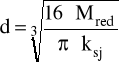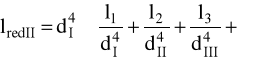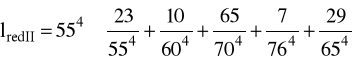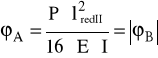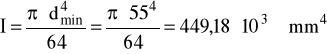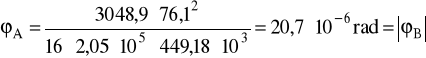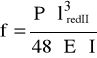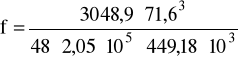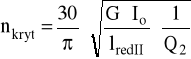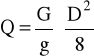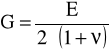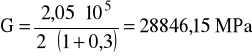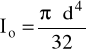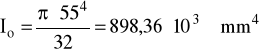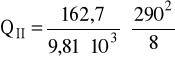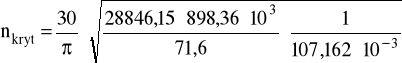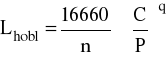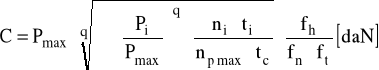Dane:	Obliczenia:	Wyniki:
u = 3,9 n1=135[obr/min] P = 7,5 kW KA = 1,4 a = 315 mm u = 3,9 m = 6 β^I = 24^0 7^I d1= 144,63mm d2= 565,37mm ap = 355 mm n1=135[obr/min] d1= 144,63mm T1 = 530,55 Nm YF1 = 4,5 b = 125 mm n2=34,61[obr/min] d2= 565,37mm T2 = 2070 Nm N c = 478,2 N σHlim =1323,16 MPa SHmin = 1,1 ZN = 0,818 ZL = 1,086 mm^2/s ZR = 1,001 ZX = 1,0 ZV = 0,976 ZW = 1,07 σH1 = 882,844 N/mm^2 σH2 = 678,468 N/mm^2 T1 = 229,2 Nm aw = 225 mm b1 = 72,5 mm N = 18 kW n = 750 obr/min d1 = 160 mm P1 = 3048,9 N l = 108,5 mm Re = 800 MPa Rm = 1000 MPa X = 4 kgo = 105 MPa ksj = 115 MPa α = 0,456 Mg = 82,7 Nm Ms = 229,2 Nm Mgmax = 82,7 Nm MredI = 229,2 Nm MredII = 250,225 Nm MredII = 271,25 Nm MredIV = 292,275 Nm MredV = 208,63 Nm MredVI = 124,99 Nm MredVII = 41,35 Nm ksj = 115 MPa dI­ = 30 mm dII = 36 mm dIII = 42 mm dIV = 48 mm dV = 40 mm l1 = 23 mm l2 = 8 mm l3 = 70 mm l4 = 8 mm l5 = 23 mm E = 2,05⋅10^5 MPa I = 39,76⋅10^3 mm^4 P = 3048,9 N E = 2,05⋅10^5 MPa I = 39,76⋅10^3 mm^4 P = 3048,9 N mn = 5 mm nI = 750 obr/min E = 2,05⋅10^5 MPa ν = 0,3 d = 40 mm GI = 93,5 N DI = 160 mm QI =30,5 Io = 251,33⋅10^3 mm^4 G = 28846,15 MPa MsI = 229,2 Nm u = 1,8 P2 = 3048,9 N kgo = 105 MPa ksj = 115 MPa MsII = 412,56 Nm Mgmax = 82,7 Nm MredI = 41,35 Nm MredI = 41,35 Nm MredII = 177,72 Nm MredIII = 314,1 Nm MredIV = 450,45 Nm MredV = 437,8 Nm MredVI = 425,2 Nm MredVII = 412,56 Nm dI = 65 mm dII = 76 mm dIII = d­IV = dV 70 mm dVI = 60 mm dVII = 55 mm l1 = 29 mm l2 = 7 mm l3 = 65 mm l4 = 10 mm l5 = 23 mm P = 3048,9 N lredII = 71,6 mm dmin = 55 mm lredII = 71,6 mm lredII = 71,6 mm I = 449,18⋅10^3 mm^4 P = 3048,9 N E = 2,05⋅10^5 MPa E = 2,05⋅10^5 MPa ν = 0,3 d = 55 mm Io = 898,36⋅10^3 mm^4 lredII = 71,6 mm QII = 107,162⋅10^-3 T = 3 lata z = 3 zmiany w = 0,6 n = 750 obr/min q = 3	Założenia konstrukcyjne: 1.1 Dobór materiałów na koła: Przyjmuję, że materiały na koła będą ulepszane cieplnie do HB ≤ 350. Materiał koła zębatego przyjmuję stal 55 ulepszaną cieplnie do HBz=270 o następujących własnościach mechanicznych: Rm = 640 MPa Re = 360 MPa σHP2 = 450 MPa σFP2 = 240 MPa Na koło małe dobieram materiał z warunku jednakowej trwałości kół zębatych o twardości: HB1 = ⋅HB2 = ⋅270 = 338,75 Przyjmuję HB1= 350 Zakładam, że koło małe, zębnik, będzie wykonane ze stali stopowej konstrukcyjnej do ulepszania cieplnego 30H o następujących właściwościach mechanicznych: Rm = 900 MPa Re = 750 MPa σHP1 = 500 MPa σFP1 = 280 MPa Przyjmuję symetryczne łożyskowanie kół zębatych. Przyjmuję, że zęby nie będą korygowane, zatem αt = α0 = 20­­­^0 Wyznaczenie odległości między osiami kół . Wyznaczenie odległości między osiami kół z warunku na naciski stykowe. 2.1.1 Rozstaw osi: Wyznaczenie obrotów koła napędzanego: [obr/min] Moment skręcający na kole napędzanym. Moment skręcający na kole napędzającym. Współczynnik geometrii zarysu Współczynnik sprężystości materiałów. Do obliczeń wstępnych przyjmuję: Zε = 0,85 Zβ = 1 ZB = 1 Współczynnik szerokości przekładni. Współczynnik obciążenia. KH = KA ⋅ KV współczynnik nadwyżek dynamicznych, wewnętrznych według materiału: prędkość obwodowa [m/s] Zatem rozstaw osi wynosi: mm Przyjmuję wstępnie znormalizowaną odległość osi a = 315 mm Wyznaczenie wartości modułu i liczby zębów. Przyjmuje wartość modułu z warunku jednakowej wytrzymałości na naciski stykowe i zginanie. m = (0,016 ÷ 0,02)a m = (0,016 ÷ 0,02)⋅ 315 = 5,04 ÷ 6,3 Przyjmuję znormalizowany moduł m = 6 Obliczam liczbę zębów na kołach. Przyjmuję z1 = 22 z2 = z1⋅u = 22⋅3,9 = 85,8 Przyjmuję z2 = 86 Odległość rzeczywista między osiami. ap = mm Po zaokrągleniu ostateczny rozstaw osi wynosi: ap = 355 mm Obliczam rzeczywisty kąt pochylenia zębów. cosβ^I = stąd β^I = 24^0 7^I Wymiary geometryczne kół zębatych. Średnice podziałowe kół. d1 = d2 = Średnice głów zębów. da1 = da2 = Średnice stóp zębów. df1 = df2 = Szerokość zęba (wieńca zęba). b = Przyjmuję szerokość wieńca b = 125 mm Obliczanie naprężeń od zginania u podstawy zęba. 5.1 Naprężenia od zginania na kole małym (zębniku). σF1= Wyznaczam współczynnik obciążenia. KF1 = KA ⋅ KV1 KF1 = 1,4 ⋅ 1,004426 = 1,406197 Wyznaczam współczynnik kształtu zęba YF1 Dla zęba α = 20^0 x1 = 0 YF1 = 4,5 Naprężenia od zginania na kole małym (zębniku). σF1= Mpa σF1<<σFP1 - koło małe nie ulega zniszczeniu 5.2 Naprężenia od zginania na kole małym (zębniku). σF2= 5.2.1 Wyznaczam współczynnik obciążenia. KF2 = KA ⋅ KV2 KF2 = 1,4 ⋅ 1,0048624 = 1,406807 Wyznaczam współczynnik kształtu zęba YF1 Dla zęba α = 20^0 x2 = 0 YF2 = 3,8 Naprężenia od zginania na kole małym (zębniku). σF2= Mpa σF2<<σFP2 - koło duże nie ulega zniszczeniu Sprawdzam zęby koła małego na naciski powierzchniowe przy zakładanym czasie pracy T = 6000 h Obliczam wartość siły F działającej na ząb. N N Obliczam nacisk na zęby dla koła małego (zębnika) dla koła wykonanego ze stali c = 478,2 MPa Obliczam dopuszczalny nacisk na ząb dla koła małego dla T = 6000 h i n1 = 135 obr/min ⇒ W = 2,5 MPa p < ko - naciski powierzchniowe działające na powierzchnie uzębienia koła małego nie spowodują jego uszkodzenia Przeprowadzenie korekcji uzębienia: Określenie sumy współczynników przesunięcia w płaszczyźnie czołowej: ⋅ gdzie: - kąt przyporu na średnicy podziałowej αon = 20°, natomiast β = 0° bo zęby są proste, czyli: α­t = αon = 20° = 0,349 rad czyli: invαt = tgαt - αt = tg20° - 0,349 = 0,0149 kąt przyporu na okręgu tocznym w płaszczyźnie czołowej czyli: zatem: invαtw = tgαtw - αtw = tg28°49' - 0,503 = 0,047 zatem suma współczynników przesunięcia w płaszczyźnie czołowej wynosi: Pozorna odległość osi. a^'w = ap + Σx*m a^'w = 331 + 4,76*6 = 359,56 mm Współczynnik zbliżenia osi (współczynnik skrócenia głowy zębów) Y = (a^'w - ap)/m Y = (359,56 - 331)/6 = 4,76 Wartości współczynników przesunięcia zębnika oraz koła zębatego przyjmujemy odwrotnie proporcjonalnie do liczby zębów Wymiary geometryczne zębów i kół po dokonanej korekcji 7.5.1 Średnice kół tocznych: Średnice kół podziałowych d1 = m*z1= 6*22 = 132 mm d2 = m*z2= 6*86 = 516 mm Wysokość głowy zęba ha1 = (1+x1-Y)m = 6( 1+22 - 4,76) = Średnica kół głów (przy y = 1 i Δy = 0): da1,2 = m⋅[z1,2 + 2⋅(y + x1,2 - Δy)] czyli: da1 = 171,978 mm oraz da2 = 300 mm Średnica kół stóp: df1,2 = m⋅[z1,2 - 2⋅(y - x1,2 + 0,25)] czyli: df1 = 149,478 mm oraz df2 = 277,5 mm Wysokości stóp zębów: hf1,2 = m⋅(y - x1,2 + 0,25) czyli: hf1 = 5,261 mm oraz hf2 = 6,25 mm Wysokości głów zębów: ha1,2 = m⋅(y + x1,2 - Δy) czyli: ha1 = 5,989 mm oraz ha2 = 5 mm Rzeczywisty luz promieniowy: czyli: Liczba n zębów do pomiaru grubości zęba: czyli: n1 = 4,0, natomiast n2 = 6,944 Zatem przyjmuję n1 = 4 oraz n2 = 7 zębów Obliczenie długości W wzdłuż normalnej przy pomiarze przez n zębów: W = m⋅cos α⋅[(n1,2 - 0,5)⋅π + z1,2⋅inv α] + 2⋅x1,2⋅m⋅sin α zatem: W1 = 54,579 mm, natomiast W2 = 100,005 mm Obliczenia sprawdzające: Z warunku na rzeczywiste naprężenia stykowe mamy: gdzie: czyli: ZE - wsp. sprężystości materiału kół: gdzie: dla stali 55 liczba Poissona ν = 0,3 dla stali 45 liczba Poissona ν = 0,25 moduł Younga E1 = E2 = 2,06⋅10^-5 MPa czyli: ZH - wsp. geometrii zarysu: czyli: Zε - wsp. stopnia pokrycia: Dla przyjmuję wg [1] Zε = 2,2 Zβ - wsp. pochylenia linii zęba: ZB - wsp. zmiany krzywizny powierzchni styku - dla przełożenia u < 3,5 przyjmuję ZB = 1. Ft - nominalna siła działająca na okręgu podziałowym w płaszczyźnie czołowej: czyli mamy: , natomiast Zatem mamy: dla zębnika σH1 = 882,844 N/mm^2 dla koła z2: σH2 = 678,468 N/mm^2 Dopuszczalne naprężenia na naciski stykowe: Granica wytrzymałości zmęczeniowej na naprężenia stykowe powierzchni zęba dla obu materiałów kół wynoszą: gdzie dla FHHRC = 50 i KHHB = 300 wg [1]: wytrzymałość zmęczeniowa trwała σ^oHlim: σ^oHlim = 17⋅FHHRC + 270 = 17⋅50 + 270 = 1120 MPa grubość warstwy utwardzonej: ht = 0,2⋅m = 1 mm wymagana grubość warstwy utwardzonej: czyli: Rzeczywisty minimalny współczynnik bezpieczeństwa przyjmuję SHmin = 1,1. ZN - współczynnik trwałości: Dla materiału kół przyjmuję wg [1] bazową liczbę cykli NHlim = 100⋅10^6 cykli. Wykładnik nachylenia krzywej Wöhlera przyjmuję qH = 9. zatem: ZL - współczynnik smarowania: Wg [5] dla prędkości V = 6,5 m/s przyjmuję z [1] olej do przekładni przemysłowych Transol 75, dla którego lepkość kinematyczna ν50 = 75 ÷ 87 mm^2/s i ν100 = 12,5 mm^2/s, czyli: ZR - wsp. uwzględniający wpływ chropowatości: gdzie: Rz1,2 - średnie wartości chropowatości zębów; przyjmuję wykonanie zębów z chropowatością Ra1,2 = 0,63 μm ⇒ Rz1,2 = 2,5 μm, czyli: ZV - współczynnik prędkości: ZW - współczynnik wzmocnienia powierzchniowego: Dla wg [1] (twardość powierzchni zęba koła słabszego - z2) mamy: ZX - współczynnik wielkości zębów - wg [1] dla modułu m < 10 przyjmuję ZX = 1,0 Czyli dopuszczalne naprężenia na naciski stykowe: σHP = 1117 MPa Czyli: σH1 = 882,844 < σHP = 1117 MPa σH2 = 678,468 < σHP = 1117 MPa A zatem warunek jest spełniony. Założenia: produkcja seryjna; praca bez rewersji obrotów; Obliczenia wałów: Schemat obciążenia: Wstępne określenie długości wału: odległość koła od wewnętrznej ścianki reduktora: δ = (0,025⋅aw + 1) δ = (0,025⋅225 + 1) = 6,625 mm Ale grubość ścianki δ ≥ 8 mm, zatem przyjmuję odległość koła od ścianki δ = 8 mm. długość wału przy wstępnym założeniu szerokości łożysk B = 20 mm: l = b1 + 2⋅δ + B l = 72,5 + 2⋅8 + 20 = 108,5 mm Wyznaczenie obciążeń i wymiarów wału I: moment skręcający na wale I: siła obwodowa na kole z1: reakcje w łożyskach: Przyjmuję materiał wałka - stal 40H, dla której: Rm = 1000 MPa Re = 800 MPa Przyjmuję wykonanie obróbki cieplnej: hartowanie: 850^oC - olej; odpuszczanie: 500^oC - olej lub woda; Przyjmuję współczynnik bezpieczeństwa X = 4, czyli będziemy mieli: współczynnik redukcyjny naprężeń: moment zastępczy (dla dominujących naprężeń stycznych): MredIV = 292,275 Nm Na końcu wału, gdzie wykresy momentów wskazują 0, przyjmuję moment zginający w łożyskach równy: wartości pozostałych momentów zostaną odczytane z wykresu poprzez interpolację liniową: MredI = 229,2 Nm MredII = 250,225 Nm MredII = 271,25 Nm MredV = 208,63 Nm MredVI = 124,99 Nm obliczenie średnic wału w przekrojach I ÷ VII: Ze względu na wykonanie wpustów oraz uwzględniając nieprzewidziane obciążenia, zwiększam otrzymane wyniki o 30%, uzyskując: dI = 28,145 mm dII = 28,977 mm dIII = 29,77 mm dIV =30,524 mm dV = 27,274 mm dVI = 23,01 mm dVII = 15,9 mm obliczenie długości zredukowanej - średnice i długości odczytujemy z wykresu: lredI = 53,57 mm obliczenie kąta obrotu dla zadanego sposobu podparcia, obliczonej długości zredukowanej oraz minimalnej średnicy: E = 2,05⋅10^5 MPa - moduł Younga dopuszczalny kąt obrotu dla wałów maszynowych wynosi: ϕdop = (0,25 ÷ 2)°/mb = (0,00436 ÷ 0,0349)rad zatem: ϕA < ϕdop obliczenie strzałki ugięcia w podporach: f = 1,198⋅10^-3 mm obliczenie wartości dopuszczalnej strzałki ugięcia: fdop = (0,005 ÷ 0,01) ⋅mn fdop = (0,005 ÷ 0,01) ⋅5 fdop = (0,025 ÷ 0,05) mm zatem: f < fdop obliczenie obrotów krytycznych wału I: 1,3nkryt ≤ nI ≤ gdzie: - moduł Kirchoffa biegunowy moment bezwładności: ciężar zębnika: GI = 9,35 kg = 93,5 N zatem mamy: QI = 30,499⋅10^-6 czyli: nkryt = 20115,3 obr/min Czyli wał I przy obrotach 750 obr/min nie jest narażony na pracę przy częstotliwościach rezonansowych. Wyznaczenie obciążeń i wymiarów wału II: Siły działające na ten wał są identyczne jak na wał I, inny jest tylko moment skręcający: moment skręcający na wale II: MsII = MsI⋅u MsII = 229,2⋅1,8 = 412,56 Nm siła obwodowa na kole z2 jest równa sile na kole z1,czyli P2 = 3048,9 N reakcje w łożyskach: Przyjmuję materiał wału II taki sam jak na wał I, czyli będzie się on charakteryzował takimi samymi własnościami: moment zastępczy (dla dominujących naprężeń stycznych): MredIV = 450,45 Nm Na końcu wału, gdzie wykresy momentów wskazują 0, przyjmuję moment zginający w łożyskach równy: wartości pozostałych momentów zostaną odczytane z wykresu poprzez interpolację liniową: MredI = 41,35 Nm MredII = 177,72 Nm MredIII = 314,1 Nm MredIV = 450,45 Nm MredV = 437,8 Nm MredVI = 425,2 Nm MredVII = 412,56 Nm obliczenie średnic wału w przekrojach I ÷ VII, średnice są zwiększane dodatkowo o 30% ze względu na nieprzewidziane obciążenia oraz wykonanie rowków wpustowych: obliczenie długości zredukowanej: Z wykresu mamy średnice: dI = 65 mm dII = 76 mm dIII = d­IV = dV 70 mm dVI = 60 mm dVII = 55 mm odpowiednio na długościach: l1 = 29 mm l2 = 7 mm l3 = 65 mm l4 = 10 mm l5 = 23 mm lredII = 71,6 mm obliczenie kąta obrotu dla zadanego sposobu podparcia, obliczonej długości zredukowanej oraz minimalnej średnicy: E = 2,05⋅10^5 MPa - moduł Younga dopuszczalny kąt obrotu dla wałów maszynowych wynosi: ϕdop = (0,25 ÷ 2)°/mb = (0,00436 ÷ 0,0349)rad zatem: ϕA < ϕdop obliczenie strzałki ugięcia w podporach: f = 0,253⋅10^-3 mm obliczenie wartości dopuszczalnej strzałki ugięcia: fdop = (0,005 ÷ 0,01) ⋅mn fdop = (0,005 ÷ 0,01) ⋅5 fdop = (0,025 ÷ 0,05) mm zatem: f < fdop obliczenie obrotów krytycznych wału II: 1,3nkryt ≤ nII ≤ gdzie: - moduł Kirchoffa biegunowy moment bezwładności: ciężar koła zębatego: GII = 16,27 kg = 162,7 N zatem mamy: QII = 107,162⋅10^-3 czyli: nkryt = 554962,45 obr/min Czyli wał II przy obrotach 416,67 obr/min nie jest narażony na pracę przy częstotliwościach rezonansowych. Obliczenie łożysk: Obliczenie łożysk na wale I: Zliczona ilość godzin pracy: Lh = ilość lat × ilość zmian × 2500×w gdzie: w - stopień wykorzystania czyli: Lh = 3⋅3⋅2500⋅0,6 = 13500 h Wymagany czas pracy łożyska: q = 3 - zakładam zastosowanie łożysk kulkowych Obciążenie zastępcze wypadkowe: Pmax = V⋅X⋅Ppmax + Y⋅Pwmax V = 1 - dla nieruchomego wału; Ppmax = 3048,9 N; Pwmax = 0; X =1; Y = 0; czyli: Pmax = 1⋅1⋅3048,9 = 3048,9 N Obliczenie nośności dynamicznej: widmo obciążenia:	HB1= 350 αt = α0 = 20­­­^0 n2=34,61[obr/min] T2 = 2070 Nm T1 = 530,55 Nm ZH = 2,47 ZE = 190 Zε = 0,85 Zβ = 1 ZB = 1 V = 1.11[m/s] a = 315 mm m = 6 z1 = 22 z2 = 86 ap = 355 mm β^I = 24^0 7^I d1= 144,63mm d2= 565,37mm da1 =156,63mm da2 =577,37mm df1 = 129,63mm df2 =550,37mm b = 125 mm KF1 = 1,406197 YF1 = 4,5 σF1= 67,82 MPa KF2 = 1,406807 YF2 = 3,8 σF2= 57,188MPa N MPa MPa P1 = 3048,9 N Mgmax = 82,5 Nm kgo = 105 MPa ksj = 115 MPa α = 0,456 MredI = 229,2 Nm MredII = 250,225 Nm MredII = 271,25 Nm MredV = 208,63 Nm MredVI = 124,99 Nm dI = 21,65 mm dII = 22,29 mm dIII = 22,9 mm dIV = 23,48 mm dV = 20,98 mm dVI = 17,7 mm dVII = 12,23 mm dI = 28,145 mm dII = 28,977 mm dIII = 29,77 mm dIV =30,524 mm dV = 27,274 mm dVI = 23,01 mm dVII = 15,9 mm lredI = 53,57 mm E = 2,05⋅10^5 MPa I = 39,76⋅10^3 mm^4 ϕA = 67,09⋅10^-6 rad ϕdop= (0,00436 ÷ 0,0349)rad f = 1,198⋅10^-3 mm fdop = (0,025 ÷ 0,05) mm G = 28846,15 MPa Io = 251,33⋅10^3 mm^4 QI =30,5 nkryt = 20115,3 obr/min MsII = 412,56 Nm P2 = 3048,9 N α = 0,456 MredIV = 450,45 Nm MredI = 41,35 Nm MredI = 41,35 Nm MredII = 177,72 Nm MredIII = 314,1 Nm MredIV = 450,45 Nm MredV = 437,8 Nm MredVI = 425,2 Nm MredVII = 412,56 Nm dI = 15,9 mm dII = 25,86 mm dIII = 31,26 mm dIV = 35,26 mm dV = 34,9 mm dVI = 35,3 mm dVII = 34,24 mm lredII = 71,6 mm I = 449,18⋅10^3 mm^4 ϕA = 20,7⋅10^-6 rad ϕdop = (0,00436 ÷ 0,0349)rad f = 0,253⋅10^-3 mm G = 28846,15 MPa Io = 898,36⋅10^3 mm^4 GII = 162,7 N QII = 107,162⋅10^-3 nkryt = 554962,45 obr/min Lh = 13500 h q = 3 V = 1 Pmax = 3048,9 N

2

Akademia Górniczo - Hutnicza w Krakowie

---