LABORATORIUM MECHANIKI TECHNICZNEJ
NR GRUPY T 3		NR PODGRUPY 3			ROK AKADEMICKI 2001/02
ĆWICZENIE NR 4 TEMAT: Analiza kratownic płaskich metodą elementów skończonych.
	Imię i nazwisko		Sprawdzian pisemny	Sprawozdanie		Ocena końcowa	Uwagi:
	Krzysztof Maciejewski

Wiadomości teoretyczne

Celem ćwiczenia jest wstępne zapoznanie się z komputerową metodą wytrzymałościowej analizy konstrukcji zwaną Metodą Elementów Skończonych ( MES ) na przykładzie płaskich ustrojów kratowych.

Metoda Elementów Skończonych pozwala rozwiązać zagadnienia rozkładu naprężeń, odkształceń i temperatury w badanej konstrukcji. Uniwersalne programy komputerowe MES ułatwiają analizę statyczną a więc określanie odkształceń i naprężeń w obiektach obciążonych statycznie oraz analizę dynamiczną, czyli wyznaczanie przemieszczeń, prędkości i przyspieszeń.

Metoda Elementów Skończonych polega na:

- podziale badanego obiektu na mniejsze części;

- dokonaniu opisu przebiegu nieznanej wielkości przez każdy z elementów skończonych, zakładając znaną postać rozkładu badanej wielkości w pojedynczym elemencie;

- zbudowaniu macierzowego modelu opisującego przebieg nieznanej wielkości w całym obiekcie.

Ćwiczenie obejmuje zakres podstawowych wiadomości o płaskim stanie naprężeń, a także o układach prętów zachowujących się jak ciało sztywne zwanych kratownicami.

Gdy osie wszystkich prętów leżą w jednej płaszczyźnie wówczas mamy do czynienia z kratownicą płaską. Do rozwiązania kratownic płaskich zakładamy takie uproszczenia, aby w przekrojach prętów występowały naprężenia normalne ( siły ściskające i rozciągające ).

Pręty łączone są węzłem. Środek ciężkości węzła jest punktem przecięcia osi wszystkich prętów. Takie połączenie zapewnia wprowadzenie siły w cały przekrój pręta.

Kratownica musi być statycznie wyznaczalna zewnętrznie i wewnętrznie. Aby warunek na statyczną wyznaczalność zewnętrzną był spełniony liczba zewnętrznych podpór kratownicy nie może przekraczać trzech. Warunek na statyczną wyznaczalność wewnętrzną:

p=2w-3

gdzie: p. - liczba prętów ( sił w prętach ),

w - liczba węzłów,

Jeżeli p>2w-3 kratownica jest przesztywniona i statycznie niewyznaczalna.

Jeżeli p<2w-3 kratownica jest układem sztywnym i staje się mechanizmem.

Rozwiązywanie kratownic płaskich metodą elementów skończonych

Kratownice płaskie można rozwiązać metodą elementów skończonych. Prostą wersją programu bazującego na metodzie elementów skończonych jest program DMES. Pozwala on przeanalizować wiele wariantów danej konstrukcji. Praca konstruktora ogranicza się do narysowania modelu kratownicy i wprowadzenia danych. Istnieje możliwość podglądu struktury odkształconej oraz sprawdzenia wykresów sił i naprężeń w prętach. Program posiada funkcje ułatwiające zmianę wprowadzonych danych i modyfikację modelu. Moduł tekstowy pozwala na szybkie przeglądanie wyników w postaci liczbowej, ich selekcję oraz drukowanie wybranych wyników na drukarce.

Rozwiązywanie kratownicy płaskiej analityczną metodą równoważenia węzłów

Metodą analityczną wyznaczamy jedynie kratownice statycznie wyznaczalne. Metoda polega na wyznaczeniu reakcji podpór za pomocą trzech równań równowagi i rozpatrzeniu równowagi węzłów. Po wyznaczeniu sił we wszystkich prętach kratownicy sprawdzamy warunki dopuszczalnych naprężeń. W prętach rozciąganych

σ=S/A<=kr

gdzie: σ - naprężenia rozciągające,

S - siła,

A - przekrój pręta,

kr - dopuszczalne naprężenia rozciągające.

W prętach ściskanych może nastąpić wyboczenie jeżeli zostanie osiągnięte naprężenie krytyczne σ_kr

σ<σ_kr=P_kr/A

gdzie : P_kr - siła krytyczna, σ - naprężenia ściskające.

Aby określić deformację kratownicy należy wyznaczyć odkształcenie sprężyste

ΔL=SL/EA

gdzie : L - długość pręta, E - moduł Younga..

Przebieg ćwiczenia

W ćwiczeniu będzie przeanalizowana następująca kratownica płaska

R_XA= 9000N 5 4 4 P_y=3000N

S₄ S₄

S₅ S₆ S₇ S₃

5 6 7 3

S₅

S₆ S₇ S₃ P_y=3000

R_XA= -9000 S₁ S₁ S₂ S₂

1 1 2 2 3

Ry =-6000

o parametrach:

materiał - stal St1

dopuszczalne naprężenie rozciągające: kr = 106 * E 6 [ N / m²]

moduł Younga: E = 2.1 * E 11 [ N / m²]

pole przekroju: A = 1 * E -4[ m²]

długość prętów a = 0,4m

granica plastyczności: Re = 220 * E 6 [ N / m²]

Analiza i rozwiązanie zadanej kratownicy.

Zanim przystąpi się do rozwiązywania kratownicy, należy sprawdzić, czy jest ona statycznie wyznaczalna. Jest to warunek konieczny rozwiązania kratownicy płaskiej.

Zatem: p = 2w - 3;

Gdzie: p=7; w=5

7=2*5 - 3

Z obliczenia wynika liczba niewiadomych jest równa liczbie równań równowagi statycznej (kratownica jest statycznie wyznaczalna ) i można przystąpić do dalszych obliczeń.

Kolejnym krokiem jest wyznaczenie reakcji występujących w podporach ( korzystając z warunku równowagi sił i momentów w dowolnym układzie płaskim ). Rozkład reakcji przedstawiony jest na poniższym rysunku.

P_iX = R_X5 - R_X1 = 0

P_iY = P_y4 + P_y3 - R_y1 = 0

Następną czynnością jest obliczenie sił działających w poszczególnych prętach ( korzystając z zasady równowagi sił )

- węzeł 1

Pix = S₁ - R_X1 + S₆ ^. cos 45^o = 0

Piy = S₅+ S₆ ^. cos 45^o - Ry = 0 ** S₆=8485

- węzeł 2

Pix = S₂ -S₁ = 0 => S₂ = S₁ => S₁ = 3000

Piy = S₇ = 0 S₇=0

- węzeł 3

Pix = - S₂- S₃ ^. cos 45^o = 0

Piy = Py + S₃ ^. sin 45^o = 0 => S₃= - 4243

S₂= 3000

- węzeł 4

Pix = S₃ ^. cos 45^o- S₆ ^. cos 45^o - S₄ = 0

Piy = Py - S₃ ^. sin 45^o- S₆ ^. sin 45^o- S₇ = 0

- węzeł 5

Pix = S₄ + R_X5 =0 => S₄= - 9000[N]

Piy = S₅ =0 => S₅=0

Siły działające osiowo w prętach:

Nr pręta	1	2	3	4	5	6	7
Siła [N]	3000	3000	- 4243	- 9000	0	8485	0

Następnie należy obliczyć naprężenia osiowe w poszczególnych prętach.

Dla prętów rozciąganych ( pręty 1,2,6) trzeba skorzystać z następującej zależności :

σ = P\A

gdzie σ - oznacza naprężenie osiowe działające w pręcie

P - siła osiowa działająca w pręcie

A - pole przekroju pręta

σ₁ = 3000 / 1*10 ^-4 = 3*10 ⁷ [N/m²]

σ₂ = 3000 / 1*10^-4= 3*10 ⁷ [N/m²]

σ₃ = - 4243 / 1*10^-4 = - 4,2*10 ⁷ [N/m²]

σ₄ = - 9000 / 1*10^-4 = - 9*10 ⁷ [N/m²]

σ₆ = 8485 / 1*10^-4 = 8,4*10 ⁷ [N/m²]

Naprężenia osiowe działające w prętach:

Nr pręta	1	2	3	4	5	6	7
Naprężenia [N/m^2]	3*10^7	3*10^7	- 4,2*10 ^7	- 9*10 ^7	0	8,4*10 ^7	0

Należy sprawdzić, czy naprężenia osiowe w prętach nie przekraczają dopuszczalnych naprężeń k_r = 100 ^. 10 ⁶ =10000 ^. 10 ⁴ [N / m²]

σ₁< k_r σ₆< k_r

σ₂< k_r

.

- siłę krytyczną można obliczyć ze wzoru Eulera:

P_kr = π ²* E * J/a ² = 1,72/0,16 = 10,8

Gdzie: E - moduł Younga

J = 8.33 * 10^-13 - moment bezwładności przekroju względem osi prostopadłej do płaszczyzny wyboczenia

a - długość pręta

- Naprężenie krytyczne określone są:

σ_kr = P_kr / A [ N / m²]

σ_kr = 10,8 / 1* 10 ^-4 = 10,8*10 ⁴ [ N / m²]

- Warunkiem bezpieczeństwa jest, aby naprężenia ściskające w pręcie były mniejsze od kry tycznych;

σ₃< σ_kr

σ₄< σ_kr

- Odkształcenia sprężyste pręta kratownicy obciążonego siłą zgodnie z prawem Hooke'a wynosi:

ΔL=SL/EA

Szkic zdeformowanej struktury kratownicy i sił w prętach

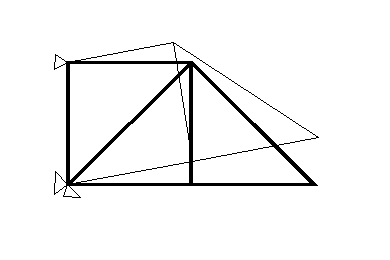
Wnioski.

Zadana kratownica jest statycznie wyznaczalna ponieważ liczba prętów (niewiadomych) jest równa liczbie równań równowagi.. W przypadku większej ilości prętów konstrukcja była by przesztywniona, natomiast w tym przypadku staje się mechanizmem, który może się deformować. W kratownicy występują siły rozciągające i ściskające działające na pręty. Naprężenia te powodują wygięcie się układu. Na rysunku widać działanie sił powodujących deformację w prętach, oraz postać zdeformowanej kratownicy.

Deformacja spowodowana jest wydłużeniem prętów, na które działają siły wewnętrzne wytworzone przez przyłożone do węzłów siły zewnętrzne i reakcje podpór. Największe siły działają w prętach 4 i 6 , pręt 4 jest ściskany natomiast 6 rozciągany. Siły te nie są jednak tak duże aby spowodować wyboczenie pręta - spełniony jest warunek bezpieczeństwa - naprężenia w prętach nie są większe od naprężeń krytycznych, które (w tym przypadku) mogą spowodować ich wyboczenie.

Wyniki obliczeń różnią się od wyników uzyskanych w programie DMES. Według tego programu w pręcie 7 powstają małe naprężenia . Z obliczeń analitycznych w pręcie tym nie występują żadne naprężenia Wynika to z niedokładności i uproszczenia obliczeń.

---