§ 8. TWIERDZENIA O WARTOŚCI ŚREDNIEJWZÓR Taylora

Twierdzenie 1 ( Twierdzenie Rolle'a )

Jeżeli funkcja f jest ciągła na przedziale domkniętym <a,b> oraz jest skończona pochodna f ' w każdym punkcie przedziału otwartego (a,b). Ponadto f(a)=f(b), to istnieje taki sam punkt
że

DOWÓD:Jeżeli
czyli
dla każdego
to wtedy
dla każdego
Jeżeli funkcja f nie jest stała na <a,b> to jako funkcja ciągła na <a,b> osiąga w nim wartość największą oraz najmniejszą. Ponieważ
więc istnieje taki punkt wewnętrzny
że jest w nim osiągana jedna z tych wartości.

Niech np. w punkcie c funkcja osiąga wartość największą. Zatem dla każdego h mamy
. Wykażemy, że
ponieważ dla h>0
dla h<0
więc z istnienia pochodnej
w każdym punkcie
wynika, że po przejściu do granicy otrzymujemy:

oraz

czyli

Twierdzenie 2 ( twierdzenie Lagrange'a )

Jeżeli funkcja f jest ciągła na przedziale domkniętym <a,b> oraz istnieje skończona pochodna w każdym punkcie przedziału otwartego (a,b) to:

gdzie

DOWÓD

Podstawiając w tezie tw. Cauchy'ego
dla
otrzymujemy

czyli

Twierdzenie 3 ( tweirdzenie Cauchy'ego )

Jeżeli funkcje f, g są ciągłe na przedziale domkniętym <a.b> oraz posiadają skończone pochodne w każdym punkcie przedziału (a,b) otwartego przy czym
dla
to

gdzie

DOWÓD Zakładamy, że
gdyż gdyby
to na mocy tw. Rolle'a pochodna g' byłaby równa zero, w pewnym punkcie
co przeczy założeniu
dla każdego
Rozważmy funkcję pomocniczą F gdzie

Funkcja F spełna założenia tw. Rolle'a gdyż:

1. F jest ciągła na <a,b> ze względu na ciągłość f , g

2. Dla każdego
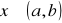
   mamy:

3. 
   

Zatem istnieje liczba
takie, że

Wnioski z twierdzeń o wartości średniej:

1. Jeżeli funkcja f jest ciągła na <a,b> oraz pochodna f' zeruje się na przedziale otwartym to f(x)=const dla
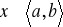
   to znaczy funkcja jest funkcją stałą na <a,b>

DOWÓD

Oznaczmy x₀ , x₀+h dowolne punkty przedziału <a,b>. Na mocy twierdzenia Lagrange'a otrzymujemy

Ponieważ z założenia
więc

2. Jeżeli funkcja f jest ciągła na przedziale <a,b> oraz posiada na (a,b) skończoną pochodną wszędzie dodatnią (wszędzie nieujemną) to funkcja f jest na tym przedziale rosnąca (malejąca)

DOWÓD

Jeżeli x₀ , x₀+h, h>0 są dodatnimi punktami przedziału <a,b> to z twierdzenia Lagrange'a wynika, że:

czyli f jest rosnąca (malejąca) na <a,b>

Twierdzenie 4 ( wzór Taylora)

Jeżeli funkcja f jest określona na przedziale domkniętym <a,b> pochodna f ^(n-1) jest ciągła na <a,b>natomiast pochodna f ⁽ⁿ⁾ (x) jest skończona dla każdego
to dla dowolnych punktów
zachodzi tzw. wzór Taylora

gdzie n= 1,2,3,4,5,6,........

przy czym reszta
może być zapisana w następujący sposób:

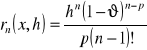
gdzie

postać Schlomlicha

postać Lagrange'a

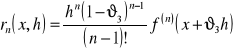
postać Cauchy'ego

DOWÓD Tw. 4 przeprowadzamy stosując Tw. Rollea

§9. EKSTREMUM FUNKCJI

Def.Mówimy, że funkcja
posiada maksimum (minimum) w punkcie
jeżeli istnieje takie otoczenie punktu

że:

(1)

Jeżeli funkcja f osiąga w x₀ maksimum (minimum) to mówimy, że f osiąga w x₀ ekstremum

W przypadku gdy w (1) lub (2) poza x₀ występuje nierówność ostra < (>) to mówimy o maksimum (minimum) właściwym

Osiąganie ekstremum przez funkcję jest własnością lokalną i może być realizowana tylko w punktach wewnętrznych przedziału określoności.

W punktach x₁ , x₃ , x₅ f osiąga minimum, natomiast w punktach x₂ , x₄ osiąga maksimum.

Twierdzenie 1 ( WARUNEK KONIECZNY ISTNIENIA EKSTREMUM )Jeżeli funkcja f posiada skończoną pochodną f ' w otoczeniu punktu
oraz posiada w tym punkcie ekstremum (minimum lub maksimum) to f '(x) = 0

DOWÓDNiech np. w x₀ istnieje maksimum funkcji f. Ponieważ pochodna f '(x) jest skończona więc:

Dla dostatecznie małych h dodatnich zachodzi nierówność:

czyli po przejściu do granicy przy
otrzymujemy:

Dla dostatecznie małych co do bezwzględnej wartości h<0 mamy:

Punkt x₀ taki, że
nazywamy punktem stacjonarnym funkcji f. Zerowanie się pochodnej funkcji f w x₀ nie wystarcza na to by w x₀ istniało ekstremum. Np. dla funkcji
gdzie

oraz

czyli f jest niemalejąca a więc brak ekstremum w x₀=0

Twierdzenie 2 ( WARUNEK DOSTATECZNY ISTNIENIA EKSTREMUM )Jeżeli funkcja f posiada w otoczeniu x₀ skończoną pochodną f ' przy czym f ' (x₀)=0 oraz istnieje skończona pochodna f '' (x₀) to:

a) w x₀ funkcja osiąga maksimum właściwe, gdy f ''(x₀)<0

b) w x₀ funkcja osiąga minimum właściwe, gdy f ''(x₀)>0

DOWÓDJeżeli f ''(x₀)<0 to na podstawie wniosku 2) z twierdzenia o wartości średniej wynika, że funkcja f ' maleje przy przejściu przez x₀. Oznacza to, że istnieje takie otoczenie
że dla
mamy:
a dla
mamy:
czyli kontynuując znów wniosek 2) stwierdzimy, że funkcja f w lewostronnym otoczeniu x₀ rośnie a w otoczeniu prawostronnym maleje. Zatem w x₀ f osiąga maksimum właściwe. Stąd część a) tezy. Podobnie dowodzimy część b) tezy.

Twierdzenie 3 ( Warunek dostateczny istnienia ekstremum )Jeżeli funkcja f posiada w otoczeniu x₀ skończoną pochodną do (n-1)-rzęduwłącznie, przy czym
oraz istnieje skończona pochodna
to w punkcie x₀nie występuje ekstremum funkcji f gdy n jest liczbą nieparzystą

a.)występuje maksimum właściwe gdzie n jest liczbą parzystą oraz

b.)występuje minimum właściwe gdy n jest liczbą parzystą oraz

DOWÓD przeprowadzamy stosując wzór Taylora Wypukłość lub wklęsłość funkcji różniczkowalnej na przedziale (a,b) podamy przy pomocy następujących twierdzeń:

Twierdzenie 4 Niech funkcja f będzie określona na przedziale (a,b) oraz posiada skończoną pochodną f '' na (a,b) Na to by funkcja f była wypukła (wklęsła) na przedziale (a,b) potrzeba i wystarcz by pochodna f ' buła niemalejąca (nierosnąca) na (a,b)

Twierdzenie 5 Niech funkcja f będzie określona na przedziale (a,b) oraz posiada skończoną pochodną f '' na (a,b)Na to by funkcja f była wypukła (wklęsła) na (a,b) potrzeba i wystarcza

Def.Mówimy, że punkt
jest punktem przegięcia krzywej y=f(x), która jest wykresem funkcji f jeżeli w x₀ zmienia się charakter wypukłości funkcji tzn. funkcja z wypukłej staje się wklęsła i na odwrót Ponieważ dla funkcji dla funkcji f określonej na przedziale (a,b) oraz posiadającej skończoną pochodną f ' na (a,b) warunkiem koniecznym i dostatecznym wypukłości (wklęsłości) funkcji f jest by f ' była niemalejącą (nierosnącą) na (a,b) więc w x₀ f ma punkt przecięcia gdy f ' osiąga w x₀ ekstremum.W ogólnym przypadku zachodzi następujące twierdzenie:

Twierdzenie 6 Jeżeli funkcja f posiada w otoczeniu x₀ skończone pochodne do (n-1)-tego rzędu włącznie przy czym
oraz skończoną pochodną n-tego rzędu
gdzie n>2to w punkcie x₀ wykres funkcji f ma punkt przegięcia gdy n jest liczbą nie parzystą.ASYMPTOTY Niech będzie dana krzywa y=f(x) określona i ciągła na
gdzie X jest przedziałem skończonym lub nieskończonym. Jeżeli odległość punku krzywej y=f(x)
od prostej dąży do zera przy
(lub
) oraz odległość ta jest stale różna od zera to prosta ta nazywa się asymptotą krzywej y=f(x)Wyróżniamy trzy rodzaje asymptot: Asymptota pozioma Na to by przy
(lub
) parzysta y=b była asymptotą krzywej y=f(x) potrzeba i wystarcza by:

b) pionowe. Jeżeli dla krzywej y=f(x) istnieje skończona pochodna f^| oraz
, lub
to prosta x=a jest asymptota pionową krzywej y=f(x)c) ukośne (pochyłe)Załóżmy, że krzywa ciągła y=f(x) posiada asymptotę o równaniu kierunkowym y=ax+b przy
. Oznaczmy przez α kąt pomiędzy osią OX i prostą y=ax+b wtedy odległość punktu P krzywej y=f(x) od asymptoty
Ponieważ
więc
oraz
przy założeniu istnienia skończonych granic. Na odwrót, jeżeli a oraz b są określone jak wyżej przy założeniu istnienia skończonych granic to prosta y=ax+b jest asymptotą krzywej y=f(x), xεX. Nazywamy ją asymptotą ukośną. Jeżeli a=0, otrzymujemy asymptotę poziomą. Analogicznie badamy asymptoty ukośne przy
. Badanie przebiegu zmienności funkcji. Dziedzina, przeciwdziedzina

Przedziały monotoniczności

Ekstrema (warunek konieczny i warunek wystarczający)

Przedziały wypukłości i wklęsłości

Punkty przegięcia

Asymptoty Tabela i wykres

18

---