Metody porzadkowania liniowego p, Wielowymiarowa analiza statystyczna, Panek, wap

Przykład 2.1

Na podstawie wystandaryzowanych wartości zmiennych diagnostycznych obliczono macierz odległości euklidesowych D przedstawioną w tablicy 2.1.

Tab. 2.1. Macierz odległości euklidesowych między województwami.

	O₁	O₂	O₃	O₄	O₅	O₆	O₇	O₈	O₉	O₁₀	O₁₁	O₁₂	O₁₃	O₁₄	O₁₅	O₁₆
O₁	0.000	2.518	3.959	2.435	2.873	3.018	2.974	3.274	4.183	3.251	3.281	3.673	4.186	3.048	3.110	1.514
O₂	2.518	0.000	3.316	2.564	3.700	2.981	3.637	4.197	4.047	2.712	2.863	3.913	2.855	1.677	2.796	2.387
O₃	3.959	3.316	0.000	4.650	4.061	4.130	4.714	5.194	3.658	4.102	4.022	4.370	2.273	3.475	4.783	3.940
O₄	2.435	2.564	4.650	0.000	3.687	3.996	4.512	3.512	5.021	3.124	3.796	5.348	4.291	2.006	4.018	2.342
O₅	2.873	3.700	4.061	3.687	0.000	3.926	3.555	3.968	5.573	4.479	3.979	3.430	3.835	3.879	4.177	3.389
O₆	3.018	2.981	4.130	3.996	3.926	0.000	2.347	2.957	3.188	2.257	2.202	4.060	3.187	3.506	2.278	3.480
O₇	2.974	3.637	4.714	4.512	3.555	2.347	0.000	3.704	4.900	4.067	2.383	4.037	4.155	4.393	3.094	3.203
O₈	3.274	4.197	5.194	3.512	3.968	2.957	3.704	0.000	4.827	2.538	4.052	5.549	4.458	4.239	3.337	4.108
O₉	4.183	4.047	3.658	5.021	5.573	3.188	4.900	4.827	0.000	3.309	3.975	5.129	3.971	4.106	4.520	4.418
O₁₀	3.251	2.712	4.102	3.124	4.479	2.257	4.067	2.538	3.309	0.000	3.463	5.019	3.218	2.880	2.546	3.790
O₁₁	3.281	2.863	4.022	3.796	3.979	2.202	2.383	4.052	3.975	3.463	0.000	4.853	3.087	2.886	3.769	2.728
O₁₂	3.673	3.913	4.370	5.348	3.430	4.060	4.037	5.549	5.129	5.019	4.853	0.000	4.591	5.033	3.621	4.461
O₁₃	4.186	2.855	2.273	4.291	3.835	3.187	4.155	4.458	3.971	3.218	3.087	4.591	0.000	2.859	3.993	4.141
O₁₄	3.048	1.677	3.475	2.006	3.879	3.506	4.393	4.239	4.106	2.880	2.886	5.033	2.859	0.000	4.019	2.512
O₁₅	3.110	2.796	4.783	4.018	4.177	2.278	3.094	3.337	4.520	2.546	3.769	3.621	3.993	4.019	0.000	3.972
O₁₆	1.514	2.387	3.940	2.342	3.389	3.480	3.203	4.108	4.418	3.790	2.728	4.461	4.141	2.512	3.972	0.000

W oparciu o macierz odległości przeprowadzono porządkowanie województw Polski, ze względu na osiągnięty poziom życia 2005 r., stosując metodę Czekanowskiego. Zakres zmienności elementów macierzy odległości został podzielony na cztery klasy, którym przyporządkowano następujące symbole graficzne:

	- do 2,5
·	- pow. 2,5 do 3,5
+	- pow. 3,5 do 4,5
X	- pow. 4,5

W kolejnym kroku w macierzy odległości D zastąpiono poszczególne jej elementy przez odpowiadające im symbole graficzne otrzymując nieuporządkowany diagram (tab. 1.5).

Tab. 2.2. Nieuporządkowany diagram Czekanowskiego.

O₁

O₂

O₃

O₄

O₅

O₆

O₇

O₈

O₉

O₁₀

O₁₁

O₁₂

O₁₃

O₁₄

O₁₅

O₁₆

O₁

•

O₂

•

O₃

•

O₄

•

O₅

•

O₆

•

O₇

•

O₈

•

O₉

•

O₁₀

•

O₁₁

•

O₁₂

•

O₁₃

•

O₁₄

•

O₁₅

•

O₁₆

•

Następnie przystąpiono do porządkowania diagramu stosując we wzorze na funkcję kryterium poprawności uporządkowania (2.1) wagi szacowane na podstawie formuły (2.2). Postać uporządkowaną wag diagramu Czekanowskiego uzyskano w 43 iteracji. Poniżej przedstawiamy postacie macierzy Czekanowskiego, w wybranych krokach procedury iteracyjnej, wraz z wartościami funkcji poprawności uporządkowania.

Krok 1

Tab. 2.3. Diagram Czekanowskiego uzyskany w kroku 1.

O₂

O₁

O₃

O₄

O₅

O₆

O₇

O₈

O₉

O₁₀

O₁₁

O₁₂

O₁₃

O₁₄

O₁₅

O₁₆

O₂

•

O₁

•

O₃

•

O₄

•

O₅

•

O₆

•

O₇

•

O₈

•

O₉

•

O₁₀

•

O₁₁

•

O₁₂

•

O₁₃

•

O₁₄

•

O₁₅

•

O₁₆

•

F¹= 224,00

Krok 2

Tab. 2.4. Diagram Czekanowskiego uzyskany w kroku 2.

O₃

O₁

O₂

O₄

O₅

O₆

O₇

O₈

O₉

O₁₀

O₁₁

O₁₂

O₁₃

O₁₄

O₁₅

O₁₆

O₃

•

O₁

•

O₂

•

O₄

•

O₅

•

O₆

•

O₇

•

O₈

•

O₉

•

O₁₀

•

O₁₁

•

O₁₂

•

O₁₃

•

O₁₄

•

O₁₅

•

O₁₆

•

F¹=226,93

Krok 20

Tab. 2.5. Diagram Czekanowskiego uzyskany w kroku 20.

O₁₆

O₄

O₁₄

O₁

O₂

O₁₀

O₁₁

O₆

O₇

O₃

O₈

O₅

O₁₃

O₉

O₁₅

O₁₂

O₁₆

•

O₄

•

O₁₄

•

O₁

•

O₂

•

O₁₀

•

O₁₁

•

O₆

•

O₇

•

O₃

•

O₈

•

O₅

•

O₁₃

•

O₉

•

O₁₅

•

O₁₂

•

F¹=251,07

Krok 42

Tab. 2.6. Diagram Czekanowskiego uzyskany w kroku 42.

O₈

O₄

O₁₅

O₁₀

O₁₄

O₁

O₂

O₁₆

O₆

O₁₁

O₇

O₁₃

O₅

O₃

O₉

O₁₂

O₈

•

O₄

•

O₁₅

•

O₁₀

•

O₁₄

•

O₁

•

O₂

•

O₁₆

•

O₆

•

O₁₁

•

O₇

•

O₁₃

•

O₅

•

O₃

•

O₉

•

O₁₂

•

F¹=262,13

Krok 43

Tab. 2.7. Uporządkowany diagram Czekanowskiego uzyskany w kroku 43.

O₈

O₁₅

O₄

O₁₀

O₁₄

O₁

O₂

O₁₆

O₆

O₁₁

O₇

O₁₃

O₅

O₃

O₉

O₁₂

O₈

•

O₁₅

•

O₄

•

O₁₀

•

O₁₄

•

O₁

•

O₂

•

O₁₆

•

O₆

•

O₁₁

•

O₇

•

O₁₃

•

O₅

•

O₃

•

O₉

•

O₁₂

•

F¹=262,40

Kolejność uporządkowania województw, ze względu na osiągnięty poziom życia w 2005 r., wskazana jest przez kolejność występowania kolumn (wierszy) diagramu opowiadających województwom.

Przykład 2.2

Stosując metodę rang przeprowadzono porządkowania województw Polski, ze względu na osiągnięty poziom życia w 2005 r. Na wstępie dokonano stymulacji zmiennych diagnostycznych X₁₁, X₁₅, X₃₅ oraz X₈₃ według formuły (1.27), dla a=0 i b=1. Następnie dokonano standaryzacji wartości zmiennych diagnostycznych w oparciu o wzór (1.31). Otrzymane wartości zmiennych diagnostycznych zawiera tablica 2.8.

Tab. 2.8. Wartość zmiennych diagnostycznych po stymulacji i standaryzacji.

Nr	Województwo	X₁₁	X₁₅	X₃₅	X₅₁	X₆₄	X₇₁	X₈₃
1	Dolnośląskie	-0.8201	0.4494	-0.0297	1.3149	0.1540	0.7433	-0.0662
2	Kujawsko-Pomorskie	-0.4350	0.4627	-0.7203	-1.0083	-0.1999	0.8002	0.3658
3	Lubelskie	-1.3763	-2.1481	0.3820	-1.0083	-0.9886	-0.3747	0.6395
4	Lubuskie	0.2781	0.8644	-1.4599	1.0567	-1.1268	1.0814	0.7602
5	Łódzkie	0.2781	-1.5456	-0.4552	1.1858	-0.2538	1.0111	-1.6879
6	Małopolskie	0.7488	0.5699	0.7029	-0.2339	0.7842	-1.0609	-0.2774
7	Mazowieckie	0.4635	-0.3004	0.4238	0.5405	2.4425	0.0471	-0.3968
8	Opolskie	2.0039	0.4895	1.2052	1.7021	-0.3886	0.0471	0.4698
9	Podkarpackie	-1.3050	0.5832	1.0099	-0.4921	-0.7729	-2.6575	0.6215
10	Podlaskie	1.0198	1.0920	0.7657	-0.3630	-0.9852	-0.3914	0.7941
11	Pomorskie	0.4635	-0.2469	-1.0622	-0.2339	1.4617	-1.0441	0.4478
12	Śląskie	-1.5475	-0.3406	0.9541	-0.6211	0.4034	0.8337	-2.8138
13	Świętokrzyskie	0.6062	-1.6125	-0.1343	-1.6537	-0.6549	-0.5354	0.2815
14	Warmińsko-Mazurskie	-0.0214	0.1682	-1.7040	-0.4921	-0.9886	0.0973	0.8165
15	Wielkopolskie	0.6917	1.3464	1.3447	-0.7502	0.5517	0.8805	-0.5643
16	Zachodniopomorskie	-1.0483	0.1682	-1.2227	1.0567	0.5618	0.5224	0.6098

W pierwszym kroku procedury porządkowania każdemu województwu przyporządkowano rangę, niezależnie ze względu na wartości kolejnych zmiennych. W kolejnym kroku obliczono wartość zmiennej syntetycznej dla każdego województwa jako średnią wartość rang według formuły (2.9). Etapy porządkowania województw zawiera tablica 2.9.

Tab. 2.9. Etapy porządkowania województw Polski, ze względu na poziom życia w 2005 r., według metody rang.

Nr	Województwo	Rangi zmiennych
Nr	Województwo			X₁₁	X₁₅	X₃₅	X₅₁	X₆₄	X₇₁	X₈₃	Średnia rang	Uporz.wojew.
1	*Dolnośląskie*	5	9	8	15	10	11	6	9,1	6
2	Kujawsko-Pomorskie	6	10	5	2,5	9	12	8	7,5	12
3	Lubelskie	2	1	9	2,5	2,5	6	13	5,1	16
4	Lubuskie	8,5	14	2	12,5	1	16	14	9,7	4
5	Łódzkie	8,5	3	6	14	8	15	2	8,1	10
6	Małopolskie	14	12	11	9,5	14	2	5	9,6	5
7	Mazowieckie	10,5	5	10	11	16	7,5	4	9,1	6
8	Opolskie	16	11	15	16	7	7,5	10	11,8	1
9	Podkarpackie	3	13	14	6,5	5	1	12	7,8	11
10	Podlaskie	15	15	12	8	4	5	15	10,6	3
11	Pomorskie	10,5	6	4	3,5	15	3	9	8,1	9
12	Śląskie	1	4	13	5	11	13	1	6,9	14
13	Świętokrzyskie	12	2	7	1	6	4	7	5,6	15
14	Warmińsko-Mazurskie	7	7,5	1	6,5	2,5	9	16	7,1	13
15	Wielkopolskie	13	16	16	4	12	14	3	11,1	2
16	Zachodniopomorskie	4	7,5	3	12,5	13	10	11	8,7	8

Przykład 2.3

Na podstawie wartości wystymulowanych, a następnie wystandaryzowanych zmiennych zawarte w tablicy 2.8 dokonano porządkowania województw Polski, ze względu na osiągnięty poziom życia w 2005 r., w oparciu o metodę sum.

W pierwszym etapie obliczono wartości zmiennej syntetycznej dla każdego województwa stosując formułę średniej arytmetycznej (2.6), przyjmując jednakowe wagi. Następnie wyeliminowano ujemne wartości zmiennej syntetycznej poprzez przekształcenie (2.10). W ostatnim kroku otrzymano, na podstawie wzoru (2.11), wartości zmiennej syntetycznej dla poszczególnych województw. Etapy porządkowania województw przedstawiono w tablicy 2.10.

Tabl. 2.10. Etapy porządkowania województw Polski, ze względu na poziom życia w 2005 r., według metody sum.

Nr	Województwo	s_i	s_i'	s_i"	uporząd-kowanie wojewó-dztw
1	Dolnośląskie	0,249	0,946	0,309	5
2	Kujawsko-Pomorskie	-0,105	0,591	0,193	10
3	Lubelskie	-0,696	0,000	0,000	16
4	Lubuskie	0,208	0,904	0,296	6
5	Łódzkie	-0,210	0,487	0,159	11
6	Małopolskie	0,176	0,873	0,285	7
7	Mazowieckie	0,460	1,156	0,378	3
8	Opolskie	0,790	1,486	0,486	1
9	Podkarpackie	-0,430	0,266	0,087	13
10	Podlaskie	0,276	0,972	0,318	4
11	Pomorskie	-0,031	0,666	0,218	9
12	Śląskie	-0,447	0,249	0,081	14
13	Świętokrzyskie	-0,529	0,167	0,055	15
14	Warmińsko-Mazurskie	-0,303	0,393	0,129	12
15	Wielkopolskie	0,500	1,196	0,391	2
16	Zachodniopomorskie	0,093	0,789	0,258	8

Przykład 2.4

W oparciu o wartości wystymulowanych i wystandaryzowanych zmiennych zawartych w tablicy 2.8 oraz wykorzystując macierz odległości przedstawioną w tablicy 2.1 dokonano porządkowania województw Polski, ze względu na osiągnięty poziom życia w 2005 r., w oparciu o miarę rozwoju.

Na wstępie wyznaczono współrzędne województwa wzorcowego w oparciu o formułę (2.13) , które przedstawiono w tablicy 2.11. Następnie obliczono odległość każdego województwa od województwa wzorcowego stosując metrykę euklidesową. Wreszcie dla każdego województwa obliczono miarę syntetyczną (2.15), według której uporządkowano województwa. Wyniki obliczeń zawiera tablica 2.12.

Tabl. 2.11. Współrzędne województwa wzorcowego.

Zmienne

z_0j

X₁₁

X₁₅

X₃₅

X₅₁

X₆₄

X₇₁

X₈₃

2,004

1,346

1,345

1,702

2,443

1,081

0,817

Tab. 2.12. Etapy porządkowania województw Polski, ze względu na poziom życia w 2005 r., według miary rozwoju.

Nr	Województwo	d_io	s_i	uporząd-kowanie wojewó-dztw
1	Dolnośląskie	4,117	0,496	5
2	Kujawsko-Pomorskie	5,060	0,381	10
3	Lubelskie	6,770	0,172	16
4	Lubuskie	4,923	0,392	9
5	Łódzkie	5,329	0,348	11
6	Małopolskie	3,857	0,528	4
7	Mazowieckie	3,134	0,617	1
8	Opolskie	3,156	0,614	2
9	Podkarpackie	6,389	0,219	15
10	Podlaskie	4,422	0,459	6
11	Pomorskie	4,480	0,452	7
12	Śląskie	6,197	0,242	14
13	Świętokrzyskie	6,054	0,259	13
14	Warmińsko-Mazurskie	5,687	0,304	12
15	Wielkopolskie	3,641	0,565	3
16	Zachodniopomorskie	4,648	0,431	8

Wartości pośrednie dla obliczeń miary rozwoju dla województw wyniosły odpowiednio:

Przykład 2.6

Na podstawie wartości zmiennych, po standaryzacji i stymulacji (tab. 2.8), oraz elementów macierzy odległości (tab. 2.1) dokonano porządkowania województw Polski, ze względu na osiągnięty poziom życia w 2005 r., w oparciu o metodę dystansową.

Na wstępie obliczono współrzędne województwa wzorcowego na podstawie formuły (2.13). Następnie oszacowano odległości każdego z województw od województwa wzorcowego stosując metrykę euklidesową (2.15). Na ich podstawie wyznaczono wartości ekstremalne odległości:

W kolejnym kroku obliczono wartości miary syntetycznej, na podstawie formuły (2.23), która stanowi podstawę porządkowania województw. Wyniki kolejnych etapów porządkowania województw zawiera tablica 2.14.

Tab. 2.14. Etapy porządkowania województw Polski, ze względu na poziom życia w 2005 r., według metody dystansowej.

Nr	Województwo	d_io	s_i	uporząd-kowanie wojewó-dztw
1	Dolnośląskie	4,117	0,270	5
2	Kujawsko-Pomorskie	5,060	0,530	10
3	Lubelskie	6,770	1,000	16
4	Lubuskie	4,923	0,492	9
5	Łódzkie	5,329	0,604	11
6	Małopolskie	3,857	0,199	4
7	Mazowieckie	3,134	0,000	1
8	Opolskie	3,156	0,006	2
9	Podkarpackie	6,389	0,895	15
10	Podlaskie	4,422	0,354	6
11	Pomorskie	4,480	0,370	7
12	Śląskie	6,197	0,843	14
13	Świętokrzyskie	6,054	0,803	13
14	Warmińsko-Mazurskie	5,687	0,702	12
15	Wielkopolskie	3,641	0,139	3
16	Zachodniopomorskie	4,648	0,416	8

Przykład 2.7

Na podstawie macierzy odległości przedstawionej w tablicy 2.1 przeprowadzono porządkowanie województw Polski pod względem poziomu życia osiągniętego w 2005 r., w oparciu o metodę Szczotki. Punktem wyjścia było uporządkowanie województw w kolejności alfabetycznej: O₁,O₂, O₃,...,O₁₆.

Dla wstępnego uporządkowania województw obliczono wartość funkcji kryterium dobroci uporządkowania (2.24), która wyniosła
=422,65 Następnie, w kroku 1, obliczono wartości funkcji kryterium dla każdej możliwej transpozycji pary województw z ich wstępnego uporządkowania. Wartość funkcji kryterium wzrosła dla transpozycji województw O₂ i O₁₂osiągając wielkość F₁=444,03. Po dokonaniu powyższej transpozycji uporządkowanie województw było następujące:

O₁, O₁₂, O₃, O₄, O₅, O₆, O₇, O₈, O₉, O₁₀, O₁₁, O₂, O₁₃, O₁₄, O₁₅, O₁₆.

Uporządkowanie powyższe stanowiło punkt wyjścia do kolejnego kroku procedury porządkowania województw.

Ostateczne uporządkowanie województw, dające maksymalną wartość funkcji kryterium porządkowania, osiągnięto w 8 iteracji. Poniżej przedstawiamy uporządkowania województw, w kolejnych krokach procedury, wraz z odpowiadającymi im wartościami funkcji poprawności uporządkowania:

Krok 2:

O₁, O₁₂, O₃, O₄, O₅, O₁₃, O₇, O₈, O₉, O₁₀, O₁₁, O₂, O₆, O₁₄, O₁₅, O₁₆.

= 457,43.

Krok 3:

O₁, O₁₂, O₃, O₄, O₅, O₁₃, O₇, O₈, O₉, O₁₀, O₁₁, O₁₅, O₆, O₁₄, O₂, O₁₆.

= 465,00.

Krok 4:

O₅, O₁₂, O₃, O₄, O₁, O₁₃, O₇, O₈, O₉, O₁₀, O₁₁, O₁₅, O₆, O₁₄, O₂, O₁₆.

= 471,06.

Krok 5:

O₅, O₁₂, O₃, O₄, O₁₆, O₁₃, O₇, O₈, O₉, O₁₀, O₁₁, O₁₅, O₆, O₁₄, O₂, O₁.

= 475,23.

Krok 6:

O₅, O₁₂, O₃, O₄, O₁₆, O₁₃, O₇, O₈, O₉, O₁₀, O₁₅, O₁₁, O₆, O₁₄, O₂, O₁.

= 478,82.

Krok 7:

O₅, O₁₂, O₃, O₉, O₁₆, O₁₃, O₇, O₈, O₄, O₁₀, O₁₅, O₁₁, O₆, O₁₄, O₂, O₁.

= 481,45.

Krok 8 (uporządkowanie ostateczne):

O₅, O₁₂, O₃, O₉, O₁₆, O₁₃, O₇, O₁₀, O₄, O₈, O₁₅, O₁₁, O₆, O₁₄, O₂, O₁.

= 483.92.

Przykład 2.8

Na podstawie wartości zmiennych diagnostycznych zawartych w tablicy 1.1 przeprowadzono porządkowanie województw Polski, ze względu na osiągnięty poziom życia w 2005 r. w oparciu o metodę gradientową. Punkt wyjścia procedury porządkowania województw stanowi przyjęty wektor wartości zmiennej syntetycznej unormowanych według formuły (1.33), dla kolejnych województw uporządkowanych alfabetycznie, o postaci:

Wartości zmiennych diagnostycznych, które zostały także poddane normalizacji według formuły (1.33), zostały przedstawione w tablicy 2.15. Następnie obliczono macierz odległości województw, w oparciu o wartości znormalizowanych zmiennych diagnostycznych (tab. 2.16).

Na podstawie wektora znormalizowanych zmiennych syntetycznych oraz macierzy odległości oszacowano wartość funkcji kryterium dobroci uporządkowania według formuły (2.27), równą
.

Dla obliczeń wartości zmiennej syntetycznej dla województw, w kolejnych iteracjach przyjęto następujące założenia:

W_max=10, W_min=1,
, liczba iteracji t=80.

Przyjmując maksymalną wartość parametru W=10 oszacowano wektor zmiennych syntetycznych w iteracji t=1 o postaci:

Wyznaczona wartość funkcji kryterium dobroci grupowania spadła w stosunku do poprzedniej iteracji (t=0) i wyniosła

W kolejnych iteracjach wektory wartości zmiennej syntetycznej oraz funkcji kryterium dobroci grupowania były następujące:

Krok 2:

Krok 3:

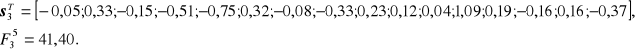
0x01 graphic

Krok 4:

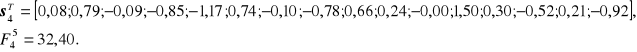
0x01 graphic

W kroku 5 wartość funkcji dobroci grupowania uległa zwiększeniu i wyniosła
W związku z powyższym powrócono do wektora wartości zmiennej syntetycznej otrzymanego w kroku 4 i zmniejszono wartość parametru W o przyjęty wskaźnik zmian (przyjęto W=5). W kroku 6 otrzymano następujący wektor wartości zmiennej syntetycznej oraz wartości funkcji dobroci grupowania:

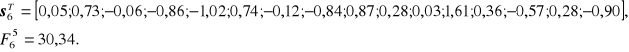
0x01 graphic

W kroku 7 wartości powyższych kategorii były następujące:

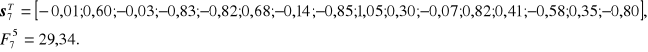
0x01 graphic

Krok 8 przyniósł wzrost wartości funkcji kryterium do
W efekcie wrócono do wartości zmiennych syntetycznych z kroku poprzedniego i zmniejszono wartość parametru W do 2,5.

W kroku 9 otrzymano:

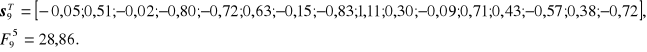
0x01 graphic

W kroku 10 wartość funkcji kryterium wzrosła do
Powrócono do wektora wartości zmiennej syntetycznej z poprzedniego kroku i zmniejszono wartość parametru W do 1,25.

W kolejnych iteracjach wartość funkcji kryterium ulegała ciągłemu spadkowi osiągając w kroku 22 wartość
przy wektorze wartości zmiennej syntetycznej:

W kroku 23 uzyskano wzrost wartości funkcji kryterium do
. Zmniejszono wartość parametru W do 0,625, jednocześnie wracając do wektora wartości zmiennej syntetycznej z poprzedniego kroku.

Krok 24 przyniósł spadek wartości funkcji kryterium do
przy wektorze wartości zmiennej syntetycznej:

W kroku 25 wartość funkcji kryterium ponownie wzrosła osiągając
. Zmniejszono wartość parametru W do 0,3125 i powrócono do poprzedniego wektora wartości zmiennej syntetycznej. Doprowadziło to do spadku wartości funkcji kryterium w kroku 26 (
) przy wektorze zmiennej syntetycznej:

Kolejna, 27 iteracja doprowadziła do wzrostu wartości funkcji kryterium (
). Ponownie zmniejszono wartość parametru W do 0,15625 i powrócono do wektora wartości zmiennej syntetycznej z poprzedniej iteracji.

W kolejnych krokach wartość funkcji kryterium stale malała osiągając w kroku 80 wartość
, przy wartościach zmiennej syntetycznej opisanej wektorem:

Wartości te wyznaczają następujące uporządkowanie liniowe województw:

O₈, O₄, O₅, O₁₆, O₁₄, O₁, O₇, O₁₁, O₂, O₆, O₁₀, O₃, O₁₅, O₁₃, O₉, O₁₂.

Tab. 2.15. Wartości zmiennych diagnostycznych po stymulacji i normalizacji.

Nr	Województwo	X₁₁	X₁₅	X₃₅	X₅₁	X₆₄	X₇₁	X₈₃
1	Dolnośląskie	0.2048	0.7433	0.5492	0.8846	0.3588	0.9096	0.7568
2	Kujawsko-Pomorskie	0.3133	0.7471	0.3227	0.1923	0.2597	0.9248	0.8758
3	Lubelskie	0.0482	0.0000	0.6842	0.1923	0.0387	0.6106	0.9512
4	Lubuskie	0.5141	0.8621	0.0801	0.8077	0.0000	1.0000	0.9845
5	Łódzkie	0.5141	0.1724	0.4096	0.8462	0.2446	0.9812	0.3101
6	Małopolskie	0.6466	0.7778	0.7895	0.4231	0.5354	0.4270	0.6987
7	Mazowieckie	0.5663	0.5287	0.6979	0.6538	1.0000	0.7234	0.6658
8	Opolskie	1.0000	0.7548	0.9542	1.0000	0.2068	0.7234	0.9045
9	Podkarpackie	0.0683	0.7816	0.8902	0.3462	0.0992	0.0000	0.9463
10	Podlaskie	0.7229	0.9272	0.8101	0.3846	0.0397	0.6061	0.9938
11	Pomorskie	0.5663	0.5441	0.2105	0.4231	0.7252	0.4315	0.8984
12	Śląskie	0.0000	0.5172	0.8719	0.3077	0.4287	0.9338	0.0000
13	Świętokrzyskie	0.6064	0.1533	0.5149	0.0000	0.1322	0.5676	0.8526
14	Warmińsko-Mazurskie	0.4297	0.6628	0.0000	0.3462	0.0387	0.7368	1.0000
15	Wielkopolskie	0.6305	1.0000	1.0000	0.2692	0.4703	0.9463	0.6196
16	Zachodnio-pomorskie	0.1406	0.6628	0.1579	0.8077	0.4731	0.8505	0.9430

Tab. 2.16. Macierz odległości euklidesowych między województwami.

	O₁	O₂	O₃	O₄	O₅	O₆	O₇	O₈	O₉	O₁₀	O₁₁	O₁₂	O₁₃	O₁₄	O₁₅	O₁₆
O₁	0.000	0.753	1.142	0.724	0.813	0.857	0.840	0.943	1.165	0.933	0.939	1.053	1.213	0.917	0.928	0.470
O₂	0.753	0.000	0.955	0.759	1.063	0.859	1.048	1.252	1.137	0.799	0.795	1.123	0.811	0.498	0.860	0.706
O₃	1.142	0.955	0.000	1.363	1.158	1.171	1.334	1.498	1.027	1.170	1.161	1.216	0.649	1.046	1.361	1.162
O₄	0.724	0.759	1.363	0.000	1.049	1.172	1.303	1.084	1.444	0.957	1.061	1.555	1.255	0.581	1.235	0.658
O₅	0.813	1.063	1.158	1.049	0.000	1.118	1.007	1.147	1.562	1.279	1.113	1.010	1.102	1.115	1.236	0.956
O₆	0.857	0.859	1.171	1.172	1.118	0.000	0.659	0.851	0.886	0.628	0.687	1.124	0.923	1.060	0.631	1.029
O₇	0.840	1.048	1.334	1.303	1.007	0.659	0.000	1.054	1.363	1.145	0.711	1.133	1.190	1.286	0.893	0.941
O₈	0.943	1.252	1.498	1.084	1.147	0.851	1.054	0.000	1.355	0.745	1.213	1.567	1.320	1.307	0.966	1.228
O₉	1.165	1.137	1.027	1.444	1.562	0.886	1.363	1.355	0.000	0.911	1.163	1.397	1.130	1.219	1.234	1.277
O₁₀	0.933	0.799	1.170	0.957	1.279	0.628	1.145	0.745	0.911	0.000	1.021	1.395	0.937	0.911	0.710	1.124
O₁₁	0.939	0.795	1.161	1.061	1.113	0.687	0.711	1.213	1.163	1.021	0.000	1.385	0.893	0.811	1.125	0.766
O₁₂	1.053	1.123	1.216	1.555	1.010	1.124	1.133	1.567	1.397	1.395	1.385	0.000	1.293	1.469	1.017	1.303
O₁₃	1.213	0.811	0.649	1.255	1.102	0.923	1.190	1.320	1.130	0.937	0.893	1.293	0.000	0.857	1.156	1.209
O₁₄	0.917	0.498	1.046	0.581	1.115	1.060	1.286	1.307	1.219	0.911	0.811	1.469	0.857	0.000	1.239	0.726
O₁₅	0.928	0.860	1.361	1.235	1.236	0.631	0.893	0.966	1.234	0.710	1.125	1.017	1.156	1.239	0.000	1.211
O₁₆	0.470	0.706	1.162	0.658	0.956	1.029	0.941	1.228	1.277	1.124	0.766	1.303	1.209	0.726	1.211	0.000

Wyszukiwarka