WAT |
LABORATORIUM RADIOELEKTRONIKI I DIAGNOSTYKI |
|||
Przedmiot: Podstawy elektrotechniki |
||||
Grupa szkolenia: |
Skład grupy:
|
Data wykonania ćwiczenia: 05-04-2012 |
Data oddania sprawozdania: 12-04-2012 |
|
|
|
Prowadzący ćwiczenie: Dr inż. Jan Szczurko |
Ocena: |
|
Temat: Badanie obwodów RLC w stanie nieustalonym |
||||
Spis treści
Spis wykresów
Spis tabel
Badanie stanu nieustalonego obwodu RLC z kondensatorem
Badanie stanu nieustalonego obwodu RLC podczas ładowania kondensatora.
Wartości doświadczalne dla:
U=20 V
R= 3MΩ
C= 8,33 µF
τ=25 s
Tabela 1
t |
0+ |
5 |
10 |
15 |
20 |
25 |
37,5 |
50 |
75 |
100 |
125 |
τ |
|
|
|
|
|
1 |
1,5 |
2 |
3 |
4 |
5 |
i |
10 |
8,4 |
7 |
5,9 |
5,1 |
4,5 |
3,4 |
2,9 |
2,4 |
2,3 |
2,3 |
Uc |
0 |
5,2 |
9,4 |
12,4 |
14,9 |
16,9 |
19,8 |
21,4 |
22,7 |
23,1 |
23,2 |
UR |
30 |
24,8 |
20,6 |
17,6 |
15,1 |
13,1 |
10,2 |
8,6 |
7,3 |
6,9 |
6,8 |
U |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
30 |
Wykres 1
Badanie stanu nieustalonego obwodu RLC podczas rozładowywania kondensatora.
Wartości doświadczalne dla:
U=20 V
R= 3MΩ
C= 8,33 µF
τ=25 s
Tabela 2
t |
0+ |
5 |
10 |
15 |
20 |
25 |
37,5 |
50 |
75 |
100 |
125 |
τ |
|
|
|
|
|
1 |
1,5 |
2 |
3 |
4 |
5 |
i |
7,76 |
6 |
4,7 |
3,6 |
2,7 |
2,1 |
1,1 |
0,5 |
0,1 |
0 |
0 |
Uc |
23,2 |
18,9 |
13,8 |
10,6 |
8,3 |
6,5 |
3,3 |
1,7 |
0,4 |
0,1 |
0 |
UR |
-23,2 |
-18,9 |
-13,8 |
-10,6 |
-8,3 |
-6,5 |
-3,3 |
-1,7 |
-0,4 |
-0,1 |
0 |
t |
0+ |
5 |
10 |
15 |
20 |
25 |
37,5 |
50 |
75 |
100 |
125 |
Wykres 2
Wnioski:
Podczas ładowania kondensatora na wykresie 1 możemy zaobserwować, iż natężenie przepływające przez obwód jest coraz mniejsze dążąc do asymptoty równej zero. Mamy tam asymptotę ponieważ z teorii wynika, że kondensator potrzebuje nieskończonego czasu aby się naładować, lecz praktycznie można zaobserwować, iż kondensator naładował nam się w przybliżeniu 125s.
W przypadku napięcia można zauważyć, że w czasie kiedy ładuje się kondensator jego spadek na kondensatorze wzrasta a na rezystancji opada dążąc do asymptot w 30V i 0V, powodem jest wcześniej wspomniany nieskończony czas ładowania. Lecz, niezależnie od zmiany napięć w obwodzie ich suma pozostaje stała.
W przypadku rozładowywania kondensatora (czyli kiedy napięcie U=0V) na wykresie 2 obserwujemy jak kondensator generuje spadek napięcia na „sobie” i na oporniku( o znaku przeciwnym do tego wygenerowanego na „sobie”). Z przepływem czasu zauważa się fakt, iż napięcie i natężenie wytworzone przez kondensator maleje do asymptoty równej zero. Jak wynika z tabeli 2 natężenie wydaje się zerować przed napięciem, lecz to jest fakt spowodowany błędem systematycznym przez zbyt mały zakres sprzętu tak jak jego wadliwość, co również jest powodem „krzywość” wykresów.
Z wykresów 1 i 2 można zaobserwować potwierdzenie 2 prawa komutacji gdyż napięcie przed i po naładowaniu kondensatora tak jak przed i po jego rozładowaniu pozostaje takie same.
Badanie stanu nieustalonego obwodu RLC z cewką indukcyjną
Badanie stanu nieustalonego w obwodzie szeregowym RL.
Wartości doświadczalne dla:
R=1KΩ
U=10V
L=100mH
τ= 100µs
Tabela 3
t |
0 |
20 |
40 |
60 |
80 |
100 |
150 |
200 |
300 |
400 |
500 |
τ |
|
|
|
|
|
1 |
1,5 |
2 |
3 |
4 |
5 |
UL |
10 |
7,7 |
6 |
4,6 |
3,6 |
3,2 |
2 |
1,2 |
0,72 |
0,6 |
0,59 |
UR |
0 |
2,3 |
4 |
5,4 |
6,4 |
6,8 |
8 |
8,8 |
9,28 |
9,4 |
9,41 |
i |
0 |
0,0023 |
0,004 |
0,0054 |
0,0064 |
0,0068 |
0,008 |
0,0088 |
0,00928 |
0,0094 |
0,00941 |
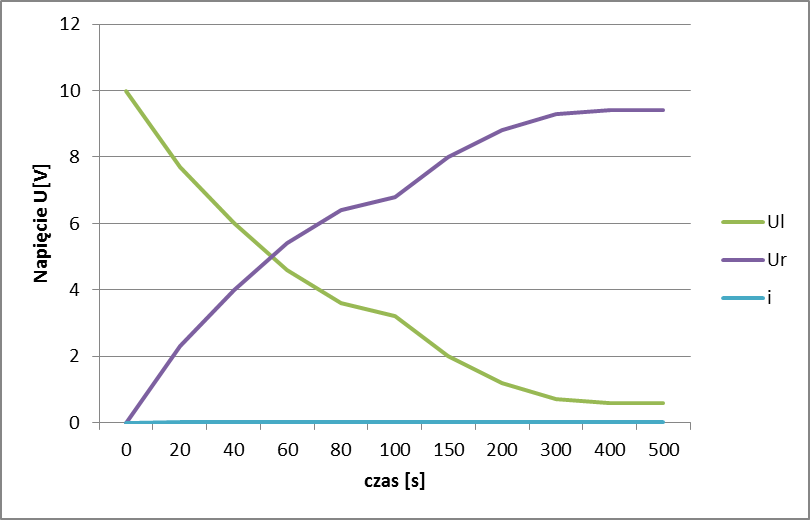
2.2Badanie stanu nieustalonego w obwodzie szeregowym RL.
Wartości teoretyczne dla:
R=1KΩ
U=10V
L=100mH
τ =100µs
Tabela 4
t |
0 |
20 |
40 |
60 |
80 |
100 |
150 |
200 |
300 |
400 |
500 |
τ |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,5 |
2 |
3 |
4 |
5 |
UL |
10 |
8,2 |
6,7 |
5,5 |
4,5 |
3,7 |
2,2 |
1,4 |
0,5 |
0,2 |
0,1 |
UR |
0 |
1,81 |
3,3 |
4,5 |
5,5 |
6,3 |
7,8 |
8,6 |
9,5 |
9,8 |
9,9 |
i |
0 |
0,00181 |
0,0033 |
0,0045 |
0,0055 |
0,0063 |
0,0078 |
0,0086 |
0,0095 |
0,0098 |
0,0099 |
e |
1 |
0,82 |
0,67 |
0,55 |
0,45 |
0,37 |
0,22 |
0,14 |
0,05 |
0,02 |
0,01 |
Wykres 4
Wnioski:
Wartości odczytane z oscyloskopu są dość zbliżone do wartości teoretycznych. Wykres dla wartości teoretycznych nie jest zbyt dokładny, wiąże się z tym mała dokładność wartości e do danej potęgi. Wartość ta była zaokrąglona do drugiego miejsca po przecinku. Wartości doświadczalne są obarczone błędami w odczycie wartości z oscyloskopów jak i poprzez wadliwy sprzęt. Pomijając te błędy i porównując ogólne wykres zależnościowe doświadczalne i teoretyczne ze skryptowymi można stwierdzić ich słuszność. Na wykresach 3 i 4 można zaobserwować słuszność 1 prawa komutacji gdyż prąd i nie zmienia się skokowo.
1
Wykres 3
Wyszukiwarka