Ćwiczenie 4.

Transformata Fouriera.

Wstęp

1. Definicja transformaty Fouriera.

Transformację Fouriera można określić jako rozszerzenie koncepcji szeregu Fouriera na dowolne sygnały. Pozwala ona na badanie właściwości sygnałów w dziedzinie częstotliwości. Rozpatrzmy sygnał x(t). Równania:

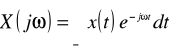
(1)

(2)

definiują parę transformat Fouriera: X(jω) jest transformatą Fouriera funkcji czasu x(t), natomiast x(t) jest odwrotną transformatą Fouriera dla sygnałuX(jω).

Rozpatrzmy prostokątny impuls pokazany na Rys.1.

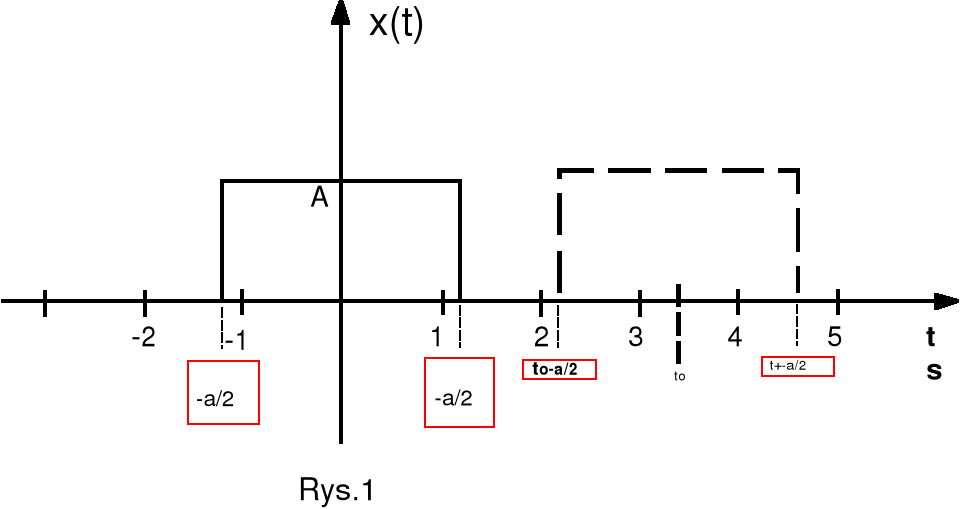
Aby wyznaczyć transformatę sygnału z Rys.1 dla t_o=0,stosujemy bezpośrednio wzór (1):

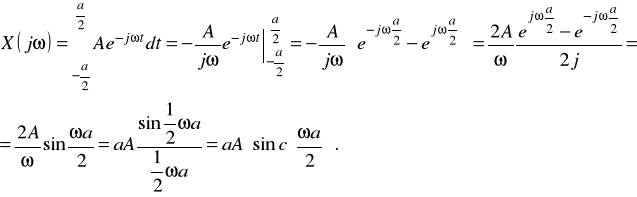
(2)

Natomiast dla dowolnej wartości przesunięcia t_o otrzymujemy:

(2)

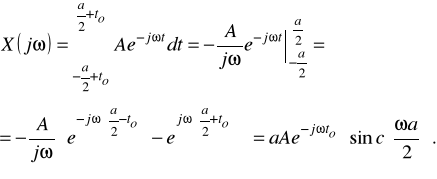
2. Jak obliczyć transformatę Fouriera i narysować odpowiednie wykresy (spektrum)?

Środowisko Matlab&Simulink dostarcza nam w tym zakresie wiele możliwości. Najprostszą metodą wyznaczania transformaty jest wykorzystanie Modułu Obliczeń Symbolicznych i uzyskanie symbolicznego opisu transformaty. Składnia podstawowej komendy wygądaja następująco:

fourier całkowa transformata Fouriera

Syntax

F = fourier(f)

F = fourier(f,v)

F = fourier(f,u,v)

Description

F = fourier(f) jest transformatą Fouriera symbolicznej wielkości (wzoru) f z domyślnie przyjętą zmienną niezależną x. Domyślną zmienną funkcji wyjściowej jest w. Czyli: transformata Fouriera stosowana jest dla funkcji zmiennej x a “zwraca” funkcję zmiennej w.

F = fourier(f,v) tworzy funkcję F symbolu v zamiast domyślnego w.

F = fourier(f,u,v) tworzy funkcję f zmiennej u oraz F zmiennej v zamiast domyślnych x i w.

Stosując następnie komendę Matlaba subs (podstawiania wartości za zmienne) można wykreślić spectrum amplitudowo-fazowe transformacji Fouriera..

PRZYKŁAD

Zakładajac, że sygnał x(t) jest dany zależnością

Oblicz transformatę Fouriera X(jω) i narysuj jej widmo amplitudowo-fazowe dla zakresu częstotliwości: -25<=ω<=25rad/s

a) Amplituda X(jω):

b) Faza X(jω):

c) Część rzeczywista X(jω),

d) Część urojona X(jω).

Rozwiązanie

m-file

% Exemplary program for plotting Fourier transform spectrum (magnitude, angle, real and imaginary parts)

% Przykładowy program do rysowania spectrum transformaty Fouriera

syms t w % uzmiennianie `symboli'

x=t*exp(-3*t)*heaviside(t); % sygnał w dziedzinie czasu

X=fourier(x,w) % Transformata Fouriera

w=-25:.1:25; % zakres częstotliwości

X=subs(X,w); % podstawienie zakresu do wzoru na transformatę

subplot(2,2,1)

plot(w,abs(X));grid on

legend('magnitude |X(jw)|')

subplot(2,2,2)

plot(w,angle(X));grid on

legend('angle <X(jw)')

subplot(2,2,3)

plot(w,real(X));grid on

legend('real of X(jw)')

subplot(2,2,4)

plot(w,imag(X));grid on

legend('imaginary of X(jw)')

result:

X =

1/(i*w + 3)^2

Przy braku Symbolic Math Toolbox, do wyznaczenia transformaty Fouriera (w postaci zboru punktów z dziedziny częstotliwości) użyta może być standardowa funkcja fft . Następujący fragment kodu ilustruje jej przykładowe wykorzystanie:

X=fft(x);

X=fftshift(X); % wyśrodkowanie częstoliwości

Xmag=abs(X);

Xmag=Xmag/max(Xmag); % normalizcja amplitudy (niekoniecznie)

Xangle=(180/pi)*angle(X);

F=[-length(X)/2:(length(X)/2)-1]*fs/length(X);

subplot(2,1,1);stem(F,Xmag);grid on;

subplot(2,1,2);stem(F,Xangle);grid on;

2. Zadania do wykonania

1. Transformata Fouriera

1. Dla sygnału z Rys Fig.1. wyznacz transformatę Fouriera i narysuj jej widmo częstotliwościowe (zastosuj komendę MATLABA fourier ). Porównaj rezultat z wzorem (4). Zmieniając czas t_o (opóźnienie sygnału), szerokość a oraz amplitudę A obserwuj kształt spektrum transformaty. Wnioski zilustruj odpowiednimi wykresami..

2. Napisz m-funkcję umożliwiającą wyznaczanie transformaty Fouriera za pomocą FFT (polecenie fftwność działania skryptu na przykładzie z poprzedniego Zadania.

3. Dane są następujące dwa sygnały:

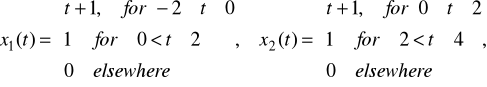
Wykreśl ich przebieg, wyznacz Transformatę Fouriera oraz narysuj odpowiednie widma częstotliwościowe. Porównaj i skomentuj uzyskane wyniki.

4. Sformułuj i potwierdź komputerowo (odpowiednią symulacją) następujące właściwości Transformaty Fouriera:

1. Liniowość

Uwaga: Zastosuj sygnały przykładowe : x(t)=exp(-3t)*u(t), x₂(t)=t*exp(-t)*u(t)

2. Przesunięcie w dziedzinie czasu.

Uwaga: Zastosuj sygnał przykładowey: x(t)=cos(t) l

3. Przesuni ęcie w dziedzinie częstotliwości

Uwaga:Zastosuj przykładowy sygnał: x(t)=t³ oraz ω_o=2

4. Zmiana skali (skalowanie w dziedzinie czasu)

Uwaga: Użyj impulse prostokątnego z Rys.1.

5. Różniczkowaniei całkowanie w dziedzinie czasu.

Uwaga: Użyj x(t)=exp(-3t)*u(t) dla różniczkowania, x(t)=exp(t)*u(-t)

+exp(-t)*u(t) dla całkowania

6. Splot w dziedzinie czasu

Zastosuj dowolne dwa sygnały (np.prostokątny i trójkątny).

5. Wyznacz (komputerowo), oblicz (stosując wzór definicyjny i właściwości Transformaty Fouriera) oraz narysuj widmoTransformaty Fouuriera sygnału:

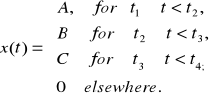
6. Wyznacz (za pomocą narzędzi symbolicznych Matlaba) transformaty Fouriera następujących funkcji:

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

1. Oblicz energię sygnału:

• W dziedzinie czasu

• W dziedzinie częstotliwości

1. TRANSMITANCJA WIDMOWA.

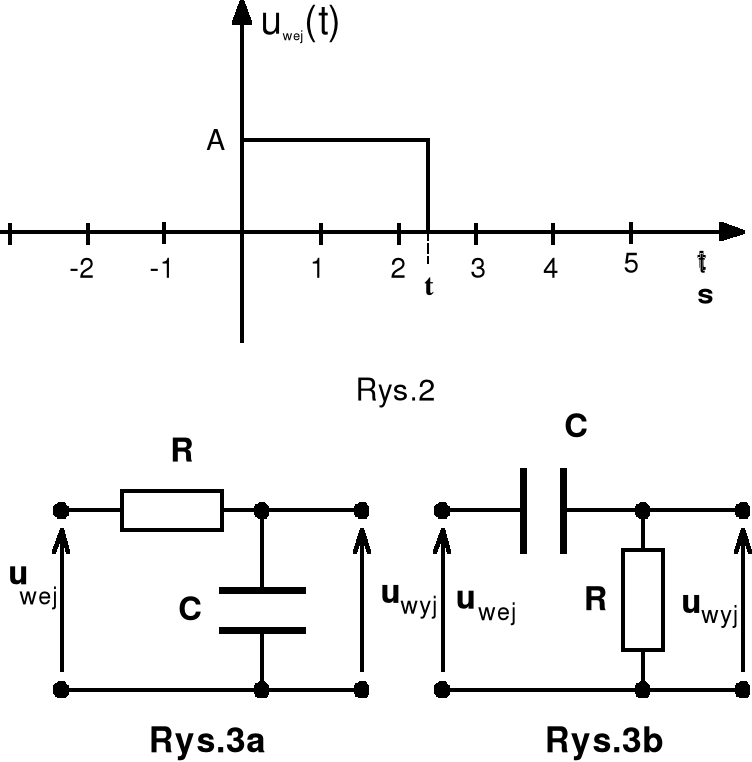
1. Sygnał z Rys.2 zasila czwórniki pokazane na Rys.3a oraz 3b. A) a) Wyznacz (narysuj) widma sygnałów wyjściowych oraz transmitancji (widmowej) dla danych: R=…..Ω, C=……F, τ=…..s).

Wskazówka: Zastosuj zarówno własne m-pliki jak i odpowiednie komendy Matlaba. Porównaj wyniki.

b) Wyznacz i narysuj odpowiedzi impulsowe obu układów.

Wskazówka: Zastosuj odpowiednią komendę Matlaba.

Jak zmiany wartości R i C (τ) wpływają na

1. odpowiedź częstotliwościową układów (transformata widmowa)?

2. widmo sygnału odpowiedzi układów?

1. Modulacja amplitudowa

Rozpatrzmy dwa najprostsze podejścia do modulacji AM:

. (3)

oraz

. (4)

gdzie
jest ciągłym sygnłem zwanym informcją (sygnał do przesłania)),
sygnałem sinusoidalym zwanym „nośną”.

1. Wyznacz spektra amplitudowe sygnału zmodulowanego i oryginalnego la następujących sygnałów informacyjnych:

a)

b) Sygnał z Rys.1 dla to=0, A=……., a=……..

Zastosuj m-pliki przygotowane wcześniej dla Zadania 2.1.2 (Matlab 5.3 oraz Matlab 2009b) lub wykładowe modele Simulinka (tylko dla użytkowników Matlaba 5.3). Odpowiedz na pytania:

1. Jak rodzaj modulacji wpływa na widmo sygnału modulowanego?

2. Jak nazywają sie (podaj również pełną I skrótową nzwą angielską!!!!) omawiane rodzaje modulacji. Opisz ich zalety i wady.

3. Skomentuj wpływ wspólczynnika α (0<α<1) na kstałt widma.

Rys.4. Przykładowa implementacja modulacji AM (I)

Rys.5. Przykładowa implementcja modulacji AM (typ II)

Niektóre potrzebne procedury:

impulse: Syntax

impulse(sys)

impulse(sys,t)

[h,t]=impulse(sys).

step: Syntax

step(sys)

step(sys,t)

[h,t]=step(sys).

Frequency response

% H(s)=(0.2s^2+0.4s+1)/(s^2+0.4s+1)

M = [1 0.4 1];

L = [0.2 0.3 1];

omega = logspace(-1,1);

freqs(L,M,omega)

Przykład :

Odpowiedź impulsowa, skokowa i na zadane wymuszenie

%Unit impulse response for system having following network function

%H(s)=s+3/(s^2+5s+6)

L=[1 3]

M=[1 5 6]

sys=tf(L,M);

Tmax=5;

td=0.1;

t=0:td:Tmax;

y1=impulse(sys,t)

y2=step(sys,t)

subplot(2,1,1);plot(t,y1);grid;ylabel('unit impulse response');

subplot(2,1,2);plot(t,y2);grid;ylabel('unit step response')

pause

%response of the system for input function x(t)=sin(t)

%Y(s)=X(s)*H(s)=(s+3)/(s^2+5s+6)(s^2+1)

L=[1 3]

M=[1 5 7 5 6]

sys=tf(L,M);

Tmax=10;

td=0.1;

t=0:td:Tmax;

y3=impulse(sys,t)

plot(t,y3);grid;ylabel('solution to x(t)=sin(t)');

1

Laboratorum Podstaw Teorii Sygnałów 2010/2011

ZUiSN PŁ

copyrights mhonwia

---