5503

Parametry geotechniczne oraz warunki gruntowe

warstwa	rodzaj gruntu	I_L	I_D	Sr	ρ [t/m³]	w_n [%]	γ [kN/m³]	C_u [kPa]	Φ_u [°]
1	Gp	0,20	-	-	2,20	12	21,58	16	14,8
2	Ps	-	0,30	0,35	1,65	6	16,19	-	31,8
3	G	0,28	-	-	2,05	21	20,11	29	16,8
4	Po	-	0,60	0,90	2,05	18	20,11	-	39,2

Parametry wytrzymałościowe całkowite ponieważ w gruncie nie występuje filtracja wód gruntowych. Ponadto dla gruntów spoistych dobrano następujące grupy konsolidacyjne:

glina piaszczysta - grupa C (zalega przypowierzchniowo i jest gruntem stosunkowo młodym, o niskim stopniu konsolidacji)
glina - grupa B (zalega dosyć głęboko i jest gruntem starszym, prekonsolidowanym)

Układ warstw geotechnicznych i geometria skarpy

Wyznaczenie profilu skarpy równostatecznej metodą Masłowa

Założenia

metoda oparta jest na hipotezie wytrzymałościowej Coulomba, w której maksymalny kąt nachylenia skarpy równostatecznej jest równy kątowi ścięcia Ψ
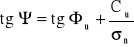
dla gruntów spoistych kąt ścięcia obliczamy ze wzoru:

gdzie : Φ_u - kąt tarcia wewnętrznego

C_u - spójność gruntu

σ_n - naprężenia normalne

dla gruntów niespoistych kąt ścięcia jest równy kątowi tarcia wewnętrznego:

tgΨ = tgΦ_u

zakładamy płaski stan odkształcenia (skarpa jest budowlą pasmową o jednym wymiarze znacznie większym niż pozostałe)

Wyznaczenie kąta nachylenia skarpy α_gen

Naprężenia pierwotne w gruncie

Przed wyznaczeniem naprężeń pierwotnych przestrzeń gruntową podzielono w obrębie warstw gruntów spoistych na warstewki obliczeniowe ( 1 m do głębokości 10 m i 2 m poniżej 10 m)

warstwa	Δh_i [m]	γ [kN/m³]	σ_n [kPa]
Gp	1,0	21,58	21,58
		1,0	21,58	43,16
		1,0	21,58	64,74
		1,0	21,58	86,32
		1,0	21,58	107,90
		1,0	21,58	129,48
Ps	2,5	16,19	169,95
G	0,5	20,11	180,00
		1,0	20,11	200,12
		2,0	20,11	240,34
Po	2,0	20,11	280,56

2.2.2. Wyznaczenie przyrostów Δx_i profilu równostatecznego skarpy

Przyrosty Δx_i obliczono ze wzoru: Δx_i = Δz_i⋅ctgΨ_i

grunt	Δz_i [m]	σ_n [kPa]	C_u [kPa]	Φ_u [°]	tgΦ_u	tgΨ	ctgΨ	Δx_i [m]
Gp	1,0	21,58	16	14,8	0,264	1,006	0,994	0,99
	1,0	43,16	16	14,8	0,264	0,635	1,575	1,57
	1,0	64,74	16	14,8	0,264	0,511	1,956	1,96
	1,0	86,32	16	14,8	0,264	0,450	2,224	2,22
	1,0	107,90	16	14,8	0,264	0,412	2,424	2,42
	1,0	129,48	16	14,8	0,264	0,388	2,579	2,58
Ps	2,5	169,95	-	31,8	0,620	0,620	1,613	4,03
G	0,5	180,00	29	16,8	0,302	0,463	2,160	1,08
	1,0	200,12	29	16,8	0,302	0,447	2,238	2,24
	2,0	240,34	29	16,8	0,302	0,423	2,366	4,73
Po	2,0	280,56	-	39,2	0,816	0,816	1,226	2,45
							ΣΔx_i =	26,27

Kąt nachylenia generalnego skarpy

Kąt nachylenia skarpy α_genobliczono ze wzoru:

tgα_gen = 0,533

α_gen = 28,05 °

Sprawdzenie stateczności skarpy przy zadanym obciążeniu metodą Felleniusa

3.1. Założenia

stan równowagi granicznej ma miejsce tylko w płaszczyźnie poślizgu
zakładamy płaski stan odkształcenia
parametry geotechniczne są niezmienne
poślizg zachodzi jednocześnie we wszystkich punktach powierzchni poślizgu
dla obliczeń klin odłamu dzielimy na bloki (które są sztywne i nie wywierają oddziaływań na sąsiednie bloki)
powierzchnia poślizgu jest powierzchnią cylindryczną przechodzącą przez dolną krawędź skarpy

Metoda Felleniusa opiera się na analizie sił występujących w paskach (blokach) gruntu, na które został podzielony klin odłamu. Zakłada się, że klin odłamu przechodzi przez dolną krawędź skarpy, a najmniej korzystny punkt obrotu klina znajduje się metodą prób (badając wartość wskaźnika stateczności F dla kilku środków obrotu, i znajdując F_min). W elementarnym pasku moment obracający jest wywołany siłą ciężkości G_i. Po przesunięciu tej siły do punktu przecięcia z płaszczyzną poślizgu, moment względem środka obrotu wywołuje składowa styczna (do powierzchni poślizgu) tej siły, która wynosi:

B_i = G_i⋅sinα_i

gdzie: α_i - kąt zawarty pomiędzy cięciwą pow. poślizgu paska a poziomem

moment utrzymujący natomiast wywołuje siła T_i wynikająca z wytrzymałości gruntu. Siłę tą działającą na powierzchnię o długości cięciwy pow. poślizgu paska i jednostkowej grubości możemy określić jako:

T_i = G_i⋅cosα_i⋅tgΦ_ui + C_ui⋅l_i

Całkowite wartości momentów dla klina odłamu otrzymuje się przez sumowanie wartości odpowiadających poszczególnym paskom. Przyjmując powyższe założenia możemy określić wartość wskaźnika stateczności jako:

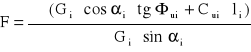
0x08 graphic

Wyznaczenie wskaźników stateczności F_i

3.2.1. Wskaźnik F1 (środek obrotu O1)

α_i [°]	sinα_i	cosα_i	h_i [m]	γ_sr [t/m³]	b_i [m]	Gq_i [kN]	tgΦ_ui	l_i [m]	C_ui [kPa]	G_ui⋅cosα_i⋅tgΦ_ui + C_uil_i	G_ui⋅sinα_i
64	0,899	0,438	6,00	21,58	2,89	187,10	0,264	6,59	16	127,15	168,16
54	0,809	0,588	8,50	18,88	1,83	250,49	0,620	3,11	0	91,29	202,65
49	0,755	0,656	9,67	19,29	1,03	180,51	0,302	1,57	29	81,28	136,23
43	0,682	0,731	12,00	19,29	2,46	1375,16	0,302	3,36	29	401,19	937,86
36	0,588	0,809	13,87	19,50	2,54	1529,67	0,816	3,14	0	1009,30	899,12
30	0,500	0,866	15,30	19,50	2,50	711,02	0,816	2,89	0	502,20	355,51
23	0,391	0,921	15,03	19,50	2,80	828,01	0,816	3,04	0	621,62	323,53
17	0,292	0,956	14,39	19,50	2,80	803,17	0,816	2,93	0	626,42	234,82
11	0,191	0,982	13,43	19,50	2,80	759,49	0,816	2,85	0	608,04	144,92
5	0,087	0,996	12,17	19,50	2,80	698,88	0,816	2,81	0	567,82	60,91
-1	-0,017	1,000	10,62	19,50	2,80	622,17	0,816	2,80	0	507,35	-10,86
-7	-0,122	0,993	8,76	19,50	2,80	529,07	0,816	2,82	0	428,29	-64,48
-14	-0,242	0,970	6,60	19,50	2,80	419,33	0,816	2,89	0	331,84	-101,44
-20	-0,342	0,940	4,10	19,50	2,80	292,11	0,816	2,98	0	223,87	-99,91
-26	-0,438	0,899	1,22	19,50	2,80	145,24	0,816	3,12	0	106,46	-63,67
-31	-0,515	0,857	0,00	19,50	1,07	12,73	0,816	1,25	0	8,90	-6,56
									Σ	6243,04	3116,80

zatem: F1 = 2,00

3.2.2. Wskaźnik F2 (środek obrotu O2)

α_i [°]	sinα_i	cosα_i	h_i [m]	γ_sr [t/m³]	b_i [m]	Gq_i [kN]	tgΦ_ui	l_i [m]	C_ui [kPa]	G_ui⋅cosα_i⋅tgΦ_ui + C_uil_i	G_ui⋅sinα_i
61	0,875	0,485	4,94	21,58	2,72	144,98	0,264	5,61	16	108,34	126,81
54	0,809	0,588	6,00	21,58	0,77	360,39	0,264	1,31	16	76,93	291,56
49	0,755	0,656	8,50	18,88	2,18	1061,40	0,620	3,32	0	431,75	801,05
42	0,669	0,743	10,37	19,29	2,04	1085,28	0,302	2,75	29	323,11	726,20
37	0,602	0,799	12,00	19,29	2,19	472,51	0,302	2,74	29	193,46	284,36
33	0,545	0,839	12,20	19,50	0,31	73,14	0,816	0,37	0	50,03	39,84
30	0,500	0,866	12,30	19,50	2,80	668,85	0,816	3,23	0	472,42	334,43
23	0,391	0,921	11,99	19,50	2,80	663,12	0,816	3,04	0	497,83	259,10
17	0,292	0,956	11,34	19,50	2,80	636,91	0,816	2,93	0	496,75	186,21
11	0,191	0,982	10,36	19,50	2,80	592,41	0,816	2,85	0	474,28	113,04
5	0,087	0,996	9,10	19,50	2,80	531,26	0,816	2,81	0	431,63	46,30
-1	-0,017	1,000	7,54	19,50	2,80	454,27	0,816	2,80	0	370,44	-7,93
-7	-0,122	0,993	5,69	19,50	2,80	361,18	0,816	2,82	0	292,37	-44,02
-13	-0,225	0,974	3,53	19,50	2,80	251,71	0,816	2,87	0	200,02	-56,62
-20	-0,342	0,940	1,04	19,50	2,80	124,76	0,816	2,98	0	95,62	-42,67
-24	-0,407	0,914	0,00	19,50	1,07	10,85	0,816	1,17	0	8,08	-4,41
									Σ	4523,07	3053,24

zatem: F2 = 1,48

3.2.2. Wskaźnik F3 (środek obrotu O3)

α_i [°]	sinα_i	cosα_i	h_i [m]	γ_sr [t/m³]	b_i [m]	Gq_i [kN]	tgΦ_ui	l_i [m]	C_ui [kPa]	G_ui⋅cosα_i⋅tgΦ_ui + C_uil_i	G_ui⋅sinα_i
56	0,829	0,559	3,41	21,58	2,34	905,10	0,264	4,18	16	200,68	750,36
48	0,743	0,669	6,00	21,58	2,31	234,54	0,264	3,45	16	96,70	174,30
41	0,656	0,755	7,07	18,88	2,87	354,10	0,620	3,80	16	226,54	232,31
34	0,559	0,829	7,48	19,29	2,80	392,94	0,302	3,38	0	98,35	219,73
28	0,469	0,883	7,46	19,29	2,80	403,47	0,302	3,17	29	199,52	189,42
24	0,407	0,914	7,43	19,29	0,29	41,65	0,302	0,32	29	20,69	16,94
21	0,358	0,934	7,02	19,50	2,80	394,49	0,816	3,00	29	387,34	141,37
15	0,259	0,966	6,30	19,50	2,80	363,64	0,816	2,90	0	286,47	94,12
10	0,174	0,985	5,29	19,50	2,80	316,41	0,816	2,84	0	254,13	54,94
4	0,070	0,998	4,01	19,50	2,80	253,89	0,816	2,81	0	206,56	17,71
-1	-0,017	1,000	2,46	19,50	2,80	176,63	0,816	2,80	0	144,03	-3,08
-7	-0,122	0,993	0,64	19,50	2,80	84,63	0,816	2,82	0	68,51	-10,31
-10	-0,174	0,985	0,00	19,50	0,90	5,62	0,816	0,91	0	4,51	-0,98
									Σ	2194,05	1876,83

zatem: F3 = 1,17

3.2.2. Wskaźnik F4 (środek obrotu O4)

α_i [°]	sinα_i	cosα_i	h_i [m]	γ_sr [t/m³]	b_i [m]	Gq_i [kN]	tgΦ_ui	l_i [m]	C_ui [kPa]	G_ui⋅cosα_i⋅tgΦ_ui + C_uil_i	G_ui⋅sinα_i
54	0,809	0,588	3,00	21,58	2,26	73,16	0,264	3,84	16	72,88	59,18
46	0,719	0,695	4,44	21,58	2,92	234,41	0,264	4,20	16	110,28	168,62
39	0,629	0,777	5,19	18,88	2,80	254,54	0,620	3,60	0	122,65	160,19
35	0,574	0,819	5,25	18,88	0,37	36,46	0,620	0,45	0	18,52	20,92
32	0,530	0,848	5,48	19,29	2,80	289,77	0,302	3,30	29	169,94	153,56
26	0,438	0,899	5,35	19,29	2,80	292,47	0,302	3,12	29	169,71	128,21
22	0,375	0,927	5,21	19,29	1,05	106,94	0,302	1,13	29	62,78	40,06
18	0,309	0,951	4,64	19,50	2,80	268,91	0,816	2,94	0	208,58	83,10
13	0,225	0,974	3,79	19,50	2,80	230,14	0,816	2,87	0	182,89	51,77
8	0,139	0,990	2,68	19,50	2,80	176,63	0,816	2,83	0	142,65	24,58
3	0,052	0,999	1,32	19,50	2,80	109,20	0,816	2,80	0	88,94	5,72
-2	-0,035	0,999	0,00	19,50	2,33	29,99	0,816	2,33	0	24,44	-1,05
									Σ	1374,26	894,85

zatem: F4 = 1,54

Minimalny wskaźnik stateczności F_min(najniebezpieczniejszy środek obrotu)

Metodą graficzną (rysunek) określono F_min= 1,14

Wnioski

Sprawdzenie stateczności metodą Felleniusa wykazało, że zaprojektowana skarpa jest stateczna ponieważ Fmin > 1 .

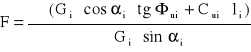
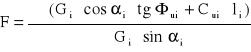
0x01 graphic

Wyszukiwarka