WZGLĘDNOŚĆ RUCHÓW . UKŁAD ODNIESIENIARuch mechaniczny - dokonująca się w czasie zmiana położenia ciała względem układu odniesienia.Właściwość polegająca na tym , ze ciało będące w ruchu względem jednego układu odniesienia może być równocześnie w spoczynku względem innego układu nazywamy względnością ruchu bądź spoczynku.Rozróżniamy następujące układy odniesienia : inercjalne i nieinercjalne.Inercjalne układy odniesienia to takie w których jest spełniona I zasada dynamiki Newtona . Jednak taki układ trudno zrealizować w praktyce. (np. układy odniesienia związane z Ziemia czy odległymi gwiazdami nie są układami inercjalnymi ze względu na to ze Ziemia i gwiazdy wykonują pewne niejednostajne ruchy jak ruch wirowy wokół własnej osi ; jednak przy omawianiu wielu zjawisk fizycznych układy te można traktować w przybliżeniu jako inercjalne.) Nieinercjalne układy odniesienia to takie w których nie jest spełniona I zasada dynamiki i dlatego występują siły bezwładności . W praktyce większość układów jest układami nieinercjalnymi.

ZASADA WZGLĘDNOŚCI GALILEUSZAx'= x - vt V'x=Vx-Vo y'=y V'y=Vy z'=z V'z=Vz a'x=ax a'y=ay a'z=az względności Galileusza:Prawa mechaniki przy przejściu z jednego układu inercjalnego do innego układu inercjalnego pozostają niezmienne.Z zasady tej wynika ze nie można za pomocą doświadczeń mechanicznych wykryć czy układ znajduje się w spoczynku czy tez porusza się ruchem jednostajnym prostoliniowym.JEDNOSTAJNIE PRZYSPIESZONYCiało porusza się ruchem jednostajnie przyspieszonym ( ze stałym przyspieszeniem ) gdy działa na nie stała siła. W ruchu tym przyrosty prędkości są wprost proporcjonalne do czasu trwania ruchu .

Równanie ruchu : x=xo+vot+at^2/2

Wzór na prędkość : v=vo+at

Prędkość średnia: vsred=( vo+v )/2

4. RUCHY NIEJEDNOSTAJNIE ZMIENNYPunkt porusza się ruchem niejednostajnie zmiennym jeżeli w ciągu jednakowych przedziałów czasu przebywa po swym torze różne drogi. Jeżeli w chwili t₁ punkt znajdował się w odległości s₁, zaś w chwili t₂ w odległości s₂ od nieruchomego punktu 0 to prędkość średnia punktu na drodze Δs=s₂-s₁, w czasie Δt=t₂-t₁ wyniesie v_śr =Δs/Δt. Jeżeli natomiast będziemy rozpatrywać coraz krótsze przedziały czasu Δt zbliżając się w granicy do zera, to prędkość średnia zbliżać się będzie do pewnej granicy, którą nazywamy predkością punktu w chwili t

A zatem prędkość w chwili t jest pochodną drogi względem czasu. Wynika z tego wniosek, że prędkość określona wektorowo w danej chwili jest zawsze styczna do toru i skierowana w kierunku ruchu punktu. Jeżeli ruch punktu jest określony równaniami parametrycznymi, to rzuty prędkości na osie prostokątnego układu współrzędnych są określone przez pochodne odpowiednich współrzędnych względem czasu: v_x=dx/dt, v_y=dy/dt, v_z=dz/dt, a prędkość punktu

Przyśpieszenie w ruchu zmiennym po linii prostej

Jeżeli torem punktu w ruchu niejednostajnie zmiennym jest linia prosta, to wektor prędkości tego punktu jest zawsze skierowany wzdłuż tej prostej. Zwrot wektora prędkości jest zgodny z kierunkiem ruchu. Jeżeli w chwili t₁ punkt miał prędkość
, zaś w chwili t₂ swą prędkość zwiększył do
, to średnie przyśpieszenie punktu wyniesie

Średnie przyśpieszenie jest więc równe przyrostowi prędkości punktu odniesionemu do jednostki czasu.

Jeżeli przedział czasu Δt będzie się zbliżać w granicy do zera to przyśpieszenie średnie zbliża się do granicy, którą nazywamy przyśpieszeniem chwilowym punktu w chwili t

A zatem przyśpieszenie w chwili t w ruchu punktu po linii prostej jest równe pochodnej predkości względem czasu. Przyśpieszenie podobnie jak prędkość jest wielkością wektorową.

Przyśpieszenie w ruchu po linii krzywej w danej chwili t jest pochodną wektora prędkości względem czasu. Przyśpieszenie
dowolnego punktu A poruszającego się po dowolnej krzywej można rozłożyć na dwie składowe: przyśpieszenie styczne
_t i przyśpieszenie normalne
_n .

Przyśpieszenie styczne ma kierunek prędkości punktu i jest równe pochodnej prędkości względem czasu a_t=dv/dt. Przyspieszenie normalne określa się zależnością a_n=v²/ρ, gdzie: v-prędkość chwilowa punktu, ρ-promień krzywizny toru w danym punkcie. Przyśpieszenie normalne jest zawsze skierowane do środka krzywizny, stąd jego druga nazwa - przyśpieszenie dośrodkowe.

Znając składowe przyśpieszenia (normalną i styczną), można wyznaczyć jego wartość ze wzoru
. Kierunek wektora przyśpieszenia wyznaczają wartości kątów, jakie wektor przyśpieszenia tworzy z kierunkiem stycznej i normalnej cos(
,t)=a_t/a, cos(
,n)=a_n/a.

Przypadkami szczególnymi ruchu niejednostajnie zmiennego są: ruch jednostajnie zmienny (w tym ruch pionowy ciała, ruch jednostajny po okręgu), rzut ukośny, ruch zmienny po okręgu itp.5. ZASADY DYNAMIKI NEWTONA DLA RUCHU POSTĘPOWEGOI zasada dynamiki : a=0 gdy Fwyp=0Każde ciało pozostaje w stanie spoczynku lub ruchu jednostajnego po linii prostej dopóty , dopóki nie zostanie zmuszone za pomocą wywierania odpowiednich sił do zmiany tego stanu .( def . równoważna : Jeśli na ciało nie działa żadna wypadkowa siła to przyspieszenie a tego ciała jest równe zeru . )Pierwsza zas . dyn . jest w istocie stwierdzeniem dotyczącym układów odniesienia . Stwierdza ona ze jeżeli w pobliżu rozważanego ciała nie ma żadnych innych ciał to można znaleźć taki zespół układów odniesienia w którym ciało nie będzie miało przyspieszenia . Fakt ze ciało pozostaje w spoczynku lub ruchem jednostajnym prostoliniowym jeśli nie przykładamy do niego żadnych sił wiążemy z własnością materii zwana bezwładnością ( inercja ). Dlatego I zasadę nazywamy często zasada bezwładności a układy odniesienia w których obowiązuje inercjalnymi . W myśl pierwszej zasady nie ma różnicy miedzy przypadkiem gdy nie działa żadna siła i przypadkiem gdy wypadkowa sił działających na ciało jest równa zero .II zasada dynamiki : Fwyp=maTempo zmiany pędu ciała jest równe sile wypadkowej działającej na to ciało . Dla ciała o stałej masie równa się to iloczynowi masy i przyspieszenia .Jeśli napiszemy a=Fwyp/m to łatwo zauważyć ze przyspieszenie ciała jest wprost proporcjonalne do wypadkowej siły działającej na to ciało i ma kierunek zgodny z kierunkiem tej siły oraz ze dla danej siły przyspieszenie jest odwrotnie proporcjonalne do masy ciała . Można tez zauważyć ze I zasada dynamiki jest szczególnym przypadkiem II zasady dynamiki ponieważ gdy Fwyp=0 to a=0 .III zasada dynamiki : Fab= - FbaKażdej akcji towarzyszy zawsze równa co do wartości lecz przeciwnie skierowana reakcja ; inaczej :wzajemne oddziaływanie dwóch ciał jest zawsze równe co do wartości lecz przeciwnie skierowane , ponadto obie te siły działają wzdłuż prostej łączącej oba ciała .Siły akcji i reakcji które zawsze występują parami działają na rożne ciała . Gdyby działały na to samo ciało nigdy nie moglibyśmy nadać żadnemu ciału przyspieszenia ponieważ wypadkowa siła działająca na każde ciało byłaby wówczas równa zeru

.6. ZASADA ZACHOWANIA PĘDUJeżeli wypadkowa sił zewnętrznych działających na układ jest równa zeru to całkowity wektor pędu tego układu pozostaje stały .Całkowity pęd układu może być zmieniony tylko przez siły zewnętrzne działające na ten układ . Siły wewnętrzne równe co do wartości i przeciwnie skierowane wytwarzają równe co do wartości i przeciwnie skierowane zmiany pędu które się wzajemnie redukują .Dla układu punktów materialnych: p1+p2+...+pn=P i gdy całkowity pęd P jest stały mamy : p1+p2+...+pn=const.=PoPędy poszczególnych punktów mogą ulegać zmianom ale suma tych pędów jeżeli na układ nie działa żadna siła zewnętrzna jest stała .Pęd jest wielkością wektorowa . Równanie : p1+p2+...+pn=const.=Po jest zatem równoważne trzem równaniom skalarnym po jednym dla każdej osi współrzędnych . A wiec zasada zachowania pędu dostarcza nam trzech warunków ruchu układu do którego te zasadę stosujemy

.7. ZASADA ZACHOWANIA ENERGII W MECHANICEEnergia może być przekształcana z jednej formy w inna ale nie może być wytwarzana ani niszczona ; energia całkowita jest wielkością stała .Innymi słowy energia całkowita tzn. suma energii kinetycznej , potencjalnej , wewnętrznej i wszystkich innych rodzajów energii nie zmienia się .0=ΔK+∑ΔU+Uwew+( zmiana innych form energii )Pojęcie energii uogólniono tak aby obejmowało ono i inne formy energii a nie tylko łatwe do zaobserwowania : energie kinetyczna i energie potencjalna . W ten sposób mechanika ciął znajdujących się w ruchu została związana ze zjawiskami niemechanicznymi w których ruchu pośrednio nie wykrywamy . Mechanika przeniknęła zatem do wszystkich działów fizyki a pojęcie energii stało się jednym z najbardziej ogólnych pojęć w fizyce .

9. SIŁY BEZWŁADNOŚCI

Rodzaje sił bezwładności : → →

I . wynikające z przyspieszenia Fb= -mau

II . wynikające z ruchu po okręgu : Fb=mar ar=V^2/R

III . siła Coriolisa : Fc=2m( v x ω )

Siły bezwładności zwane tez pozornymi wprowadzamy wówczas gdy chcemy stosować mechanike klasyczna do nieinercjalnych układów odniesienia . Siły te nie są wywierane na ciało przez żadne z ciał znajdujących w jego otoczeniu . Po prostu ich wprowadzenie pozwala na stosowanie zasad mechaniki klasycznej w układach poruszających się z przyspieszeniem . W układach inercjalnych te siły znikają .

10. SIŁA CORIOLISASiła Coriolisa związana jest ze zmianą układów odniesienia. Zauważa się ją przy przejściu z inercjalnego układu odniesienia do układu nieinercjalnego. Zalicza się ja do sił pozornych. Rozważmy ruch człowieka idącego na karuzeli w kierunku radialnym. Dla obserwatora stojącego na ziemi (układ inercjalny) na człowieka idącego po karuzeli działają siły: radialna - związana z przyspieszeniem dośrodkowym i styczna - związana z przyśpieszeniem Coriolisa (a=2ωv_r). Przyśpieszenie Coriolisa wynika ze zmiany kierunku wektora prędkości radialnej, oraz zmiany kierunku i wartości wektora prędkości stycznej. Obserwator stojący na karuzeli nie widzi jednak żadnego z tych przyspieszeń; idący po karuzeli człowiek, znajduje się względem niego w równowadze i rzeczywistą siłę tarcia działającą na poruszającego się człowieka równoważy siłami pozornymi - odśrodkową, działającą radialnie na zewnątrz i styczną - nazwaną siłą Coriolisa, która działa w kierunku przeciwnym do kierunku obrotu karuzeli. Siłę Coriolisa oblicza się ze wzoru F_c =2mωv_r.

11. FIZYCZNE SKUTKI WYSTĘPOWANIA SIŁY CORIOLISASkutki występowania siły Coriolisa :Dla ciał poruszających się w kierunku poziomym wzdłuż południka wartość siły Coriolisa wynosi Fc=2mvωsinϕ, gdzie ϕ jest szerokością geograficzna . Na półkuli północnej siła ta działa w prawo w stosunku do kierunku ruchu na półkuli południowej w lewo. Powoduje to np. ze rzeki płynące na półkuli północnej wzdłuż południków silniej podmywają prawy brzeg. Siła Coriolisa wpływa tez na kierunek wiatrów. Masy powietrza płynące nad Ziemia od wyżu do niżu są na półkuli północnej odchylane w prawo na południowej w lewo . Przy dużych zmianach ciśnienia prowadzi to do powstania silnych wirów czyli cyklonów ( przy ruchu mas powietrza do centrum niżu ) i antycyklonow ( przy odpływie mas powietrza od centrum wyżu ). Siła Coriolisa powoduje również , ze podzwrotnikowe wiatry tzw. pasaty wiejące z obszarów podzwrotnikowych w kierunku równika są odchylane na półkuli północnej w prawo , na południowej w lewo .

12 . POSTULATY SZCZEGÓLNEJ TEORII WZGLĘDNOŚCISzczególna teoria względności zaproponowana w 1905r. przez Einsteina jest oparta na dwóch postulatach .I postulat : Prawa fizyki maja jednakowa postać we wszystkich inercjalnych układach odniesienia . Nie istnieje żaden wyróżniony inercjalny układ odniesienia, lub innymi słowy jednostajny i prostoliniowy ruch odosobnionego układu ciał jako całości nie ma wpływu na prawa opisujące dowolne zjawiska zachodzące w tym układzie; czyli za pomocą żadnych dośw. Nie można stwierdzić czy układ ten spoczywa czy też porusza się jednostajnie prostoliniowo. II postulat :Prędkość światła jest jednakowa we wszystkich inercjalnych układach odniesienia . Pierwszy postulat stanowi zasadę względności , która jest uogulnieniem na dowolne zjawisko fizyczne zasady względności Galileusza obowiązującej w mechanice. Obydwa posyulaty są bezspornie potwierdzone przez liczne doświadczenia. Einstein obalił pojęcie a priori dotyczące czasu , które wysunięte były przez Newtona . Newton był przekonany o istnieniu czasu absolutnego niezależnego od jakichkolwiek czynników zewnętrznych .

14 . PARAMETRY STANU GAZU

Równanie stanu gazu doskonałego ( kilka wersji ) :

p=nkT

p - ciśnienie ; n - koncentracja ; k - stała Boltzmana ; T - temperatura

pV/T=Nk

V - objętość ; N - liczba cząsteczek

Dla danej liczby cząsteczek gazu iloczyn jego ciśnienia i objętości podzielony przez jego temperaturę bezwzględną jest wartością stałą .

pV/T=constans

Zmiana któregokolwiek z parametrów p,V,T musi spowodować zmianę pozostałych czynników w taki sposób by wyrażenie pV/T nie uległo zmianie .

Równanie Clapeyrona :

pV= ( m/μ )RT

m - masa gazu ; μ - masa cząsteczkowa

Przemiany stanu gazu :

- izotermiczna ( T=const )

W izotermicznej przemianie stałej masy gazu ciśnienie wywierane przez gaz na ścianki naczynia jest odwrotnie proporcjonalne do jego objętości .

pV=const

- izobaryczna ( p=const )

W izobarycznej przemianie stałej objętość zmienia się wprost proporcjonalnie do temperatury

V/T=const

- izochoryczna ( V=const )

W izochorycznej przemianie stałej masy gazu jego ciśnienie zmienia się wprost proporcjonalnie do temperatury

p/T=const

Przemiana adiabatyczna :

Zmianę stanu w której nie ma wymiany ciepła z otoczeniem nazywamy przemiana adiabatyczna .

pV^k=const k -pewien współczynnik wyznaczany eksperymentalnie

Prędkość średnia cząsteczek : <v>=sqrt 8kT/Πm=sqrt 8RT/Πμ

sqrt - pierwiastek , m - masa 1 cząstki gazu , R - stała gazowa

Prędkość najbardziej prawdopodobna : vp=sqrt 2kT/m = sqrt 2RT/μ

Średnia prędkość kwadratowa : sqrt <v^2>=sqrt 3kT/m =sqrt 3RT/μ

Średnia energia kinetyczna 1cząstki : <ε>=3kT/2

Średnia droga swobodna : λ=1/(sqrt2)nσ σ=Πr^2 ( przekrój czynny )

Temperatura jest miara średniej energii kinetycznej ruchu postępowego cząsteczek gazu .

15.Założenia kinetyczno-molekularnej teorii gazów doskonałych

Teoria molekularna zakłada, że gaz składa się z bardzo dużej lecz ściśle określonej ilości idealnie sprężystych cząsteczek które poruszają się ze znacznymi szybkościami zderzając się wzajemnie oraz uderzając o ścianki zbiornika w którym gaz jest zawarty. Ponieważ nie jest możliwe oddzielne badanie ruchu każdej cz. w celu uproszczenia zjawiska cząsteczki gazu rzeczywistego zastępujemy punktami materialnymi. Przyjmujemy także , że idealnie sprężyste cząsteczki gazu poruszają się chaotycznie tzn. , że każde położenie i kierunek ruchu cz. jest jednakowo prawdopodobny (Cząsteczki te są w ciagłym, bezustannym i chaotycznym ruchu.). Ponadto zderzenia między cząsteczkami są idealnie sprężyste (spełnione są dwie zasady: zachowania pędu i energii.) i oddziaływują ze sobą tylko w momencie zderzenia

.16 .Podstawowy wzór kinetyczno-molekularnej teorii gazu

Wobec tego, że ruch cząsteczek jest całkowicie chaotyczny ,możemy przyjąć że(średnio biorąc)1/3 całkowitej liczby cząsteczek gazu, porusza się między przeciwległymi ściankami naczynia.t₁-czas potrzebny na to aby liczba uderzeń cz. o ściankę była równa 1/3N t₁=2l/<v> l- długość krawędzi sześcianu. (W tym czasie ze ścianą naczynia o wartość 2m<v>).Wczasie t₁ ,1/n cz.dozna łącznej zmiany pędu rownej 1/3N2m<v>.W tym samym czasie cz.te udzielą ściance popędu siły równego zmianie pędu: F_srt₁=2/3Nm<v>, F_sr2l/<v>=2/3Nm<v>, F_srl=2/3m.<v><v>/2, F_sr/l²=2N/3V<E>, F_sr/l²=p.,N/V=n -liczba molekuł w jednostce objętości, p=2/3 n<E> lub inaczej pV=2/3N<E> (podstawowy wzór teorii kin-mol t g ) pV=m/μRT=N/N_aRT, N/N_aRT=2/3N<E>, <E>=3/2kT,R-st. gazowa=8.31 J/(mol K),N_a-l.Avogarda,R/N_a=st.Boltzmanna,k=1,38*10^-23[J/K].

17. Prawo rozkładu predkości cząsteczek gazu Dla danego gazu istnieje charakterystyczny rozkład prędkości cząsteczek. Maxwell jako pierwszy rozwiązał zagadnienie najbardziej prawdopodobnego rozkładu prędkosci wielkiej liczby cz gazu. Prawo rozkładu N-cząst. dla próbki gazu zawierającej .N-cząsteczek ma postać: N(v)=4ΠN(m/2ΠkT)^3/2v²e^-(mvv/2kT), N(v)dv- l.cz mających prędkości zawarte między v a v+dv, T-temp,k-stałaBoltzmana m.-masa. Wniosek: Dla danego gazu rozkład prędkości zależy tylko od temp.

18. Prędkości charakterystyczne rozkładu MaxwellaPrędkości charakterystyczne rozkładu Maxwella: 1.v najbardziej prawdopodobna v_p-prędkośc najw. liczby molekuł. Dla tej wartości prędkości funkcja rozkładu osiąga max.;v_p(2kT/m.)^o.5 lub v_p=(2RT/μ)^o.5 μ-masa mol.gazu.2)v średnia <v>=(8kT/Πm)^o.5,v śr. jest nieco większa od prędkości najbardziej prawdopodobnej ponieważ liczba molekuł o prędkościach większych od v_p niż l.mol. o v mniejszych; 3)v śr kwadratowa jest równa pierwiastkowi kw.ze średniej warości kwadratów v.√(<v>²) =√(3kT/m); v śr.kw.jest większa niz prędkośc śr.(uzasadnienie jak wyżej)

19.Wzór barometryczny Boltzmana jest szczególnym przypadkiem funkcji rozkładu Boltzmanna .Określa on zależnośc ciśnienia atmosferycznego od wysokości na poziom morza: p=p_oe^-(mgh/kt).Cisnienie powietrza, a więc i koncentracja molekuł maleje wykładniczo ze wzrostem wysokości czyli ze wzrostem en .pot. molekuł w polu grawitacyjnym ziemi.

20.Równanie przewodnictwa ciepła .Przenoszenie energii wywołane różnicą temperatur między sąsiednimi częściami ciała nazywamy przewodnictwem cieplnym, Podstawowe prawo przewodnictwa cieplnego :dQ/dt=-κSdT/dx (dQ/dt-szybkość przepływu ciepła przez pow. S; dT/dx-gradient temp.,κ-współczynnik. Proporcjonalności. tzw przewodność. cieplna [w/mK])21.Równania dyfuzji i transportu(lepkość); Dyfuzja-samorzutnie przebiegający proces wyrównania koncentracji molekuł na skutek ich ruchu cieplnego: D=1/3λ<v>; <v>-pr.śr, <v>=√(8kT/Πm.),λ-sr dr swobodna ,λ=kT/(√2σp.), σ-przekrój czynny na zderzenie ,p. cisnienie gazu,D~1/p.,D~T^3/2;Ze wzoru wynika również że im molekuły mają większe masy i większe rozmiary tym dyfunduja wolniej. Transport pędu-wystepuje między warstwami gazu o róznej prędkoσci w ruchu uporządkowanym :η=1/3<v>λ!,η-wsp.lepkości,wsp lepkości nie zależy od stopnia koncentracji molekuł natomiast η~T^3/222.Odległość jaką przebywa molekuła miedzy dwoma zderzeniami nazywa się droga swobodną l ,a śr. wartość tej odległości jest sr. droga swobodną <l>;<l>=1/(√2nσ),n-koncentracja gazu ,σ-przekrój czynny)

23.Konwekcja(unoszenie)- Gdy jakaś część cieczy lub gazu zostaje ogrzana rozszerza się ona a gęstość maleje, w skutek czego cieplejsza porcja cieczy lub gazu unosi się do góry zaś z sąsiednich miejsc napływają chłodniejsze warstwy. Powoduje to powstawanie prądów które stykając się z przedmiotami chłodniejszymi oddają im ciepło ogrzewając je w ten sposób. Tak prądy powietrza powstające w pokoju po napaleniu w piecu roznoszą ciepło oddając je ścianom sufitowi i przedmiotom znajdującym się wpomieszczeniu. Zjawisko to nazywamy konwekcją czyli unoszeniem ciepła. KONWEKCJA proces przenoszenia en w skutek unoszenia Zjawisko występowania pionowych prądów w cieczach i gazach wywołane różnica temperatur poprzez cieplną zmianę ciężaru właściwego. Prądom konwekcyjnym towarzyszy konwekcja ciepła ,unoszenie ciepła przez masę gazu: KONWEKCJA=DYFUZJA+WYMIANA CIEPŁA(przewodnictwo).

24.Prawo Pascala-Rozważamy cylinder zamknięty tłokiem wypełniony cieczą na który działamy ciśnieniem zewnętrznym p₀ . W każdym dowolny, punkcie P. znajdującym się w odległości a od górnej powierzchni ciśnienie p. dane jest wyrażeniem p.=p₀+ρgh ρ-gęstość p.-ciśnienie. Powiększmy ciśnienie zewnętrzne o dowolną wartość Δp₀. Ponieważ ciecze w istocie swojej są nieściśliwe więc gęstość ρ w powyższym związku pozostaje praktycznie stała podczas trwania tego procesu i dlatego zmiana tego ciśnienia Δp₀ w dowolnym punkcie P. równa się Δp₀ To prawo zostało nazwane prawem Pascala, która brzmi: Ciśnienie wywierane na zamknięty płyn jest przekazywane nie zmienione na każdą część płynu oraz na ścianki naczynia. P.P jest słuszne dla cieczy w stanie równowagi. (Ciśnienie wywierane na zamkniety płyn jest przrekazywane jednakowo na każdą część płynu oraz na ścianki naczynia bez zadnych strat.Stwierdzenie to nie stanowi niezależnego prawa ale jest nieodzowną konsekwencją praw mechaniki płynów)

25.Prawo Archimedesa- Kiedy ciało jest zanurzone w całości lub częściowo w spoczywającym płynie który wywiera ciśnienie na każdą będącą z nim w kontakcie część powierzchni ciała . Wypadkowa tych wszystich sił jest skierowana ku górze i jest to tak zwana siła wyporu. Ciśnienie nie zależy od materiału z jakiego ciało jest wykonane, dlatego ciało zastąpimy przez ten sam płyn co płyn otoczenia wówczas siła wypadkowa jest równa ciężarowi płynu i jest skierowana do góry przez środek ciężkości płynu. Ciało w całości lub częściowo zanurzone w płynie wypierane jest ku górze siłą równą ciężarowi płynu wypartego przez to ciało. (Ciało w całosci lub częściowo zanurzone w płynie wypierane jest ku górze siłą równą ciężarowi płynu wypartego przez to ciało. Odpowiedni punkt ciała zanurzonego nosi nazwę środka siły wyporu.)

26. Rodzaje przepływów: -laminarny (warstwowy), wirowy, turbulentny (burzliwy) Rodzaj przepływu jest charakteryzowany liczbą przepływu lub liczbą Reynoldsa R=vdρ/η laminarny-R<500 (d<1000) Jest to przepłuw ustalony cz. płynu poruszają się w kierunku przepływu po torach równoległych .Istnieje wtedy gdy w dowolnym punkcie prędkość każdej przechodzącej przez ten punkt cząsteczki jest zawsze taka sama. Warunki takie mogą zaistnieć przy niskich prędkościach przepływu (R<500) Przepływ laminarny(ustalony)-Mowi się że ruch płynu jest ustalony kiedy prędkość płynu v jest w dowolnie wybranym punkcie stała w czasie.; Przepływ turbulentny R>1000 podczas tego przepływu praca z nim związana względem W_turb=(5 do 12) W_lamin Ruch turbulentny jest ruchem w którum oprócz przepływu równoległego pojawiają się ruch poprzeczne (jest to przrepływ płynu którego v zmienia się bezwładnie od punktu do punktu a także w czasie.)Ruch wirowy jest ruchem pośrednim R<500r-1000r)

27.Siła oporu kulki przy przepływie laminarnym (wzór Stokesa)

F=6πηrv;η-lepkość,r-promień kulki,v -predkość

28. Równanie ciągłości masyRozważmy rurkę o nieregularnym przekroju przez którą przepływa płyn. W czasie Δt element płynu przepływa w przybliżeniu odległość V*Δt. Masa Δm₁ płynu przechodzącego przez A₁ jest równa Δm₁=ρ₁A₁V₁Δt a dla A₂ podobnie czyli strumień masy Δm₁/Δt≈ρ₁A₁V₁ a Δm₂/Δt podobnie. Na to żeby ani V ani A nie zmieniały się w istotny sposób na drodze którą przebył płyn musimy wziąć Δt dostatecznie małe (dąży do 0) Strumień masy w P= ρ₁A₁V₁ a w Q=ρ₂A₂V₂ Masa płynu przepływająca w jednostce czasu musi być taka sama ponieważ żadna część płynu nie może opuścić rury zatem ρ₁A₁V₁=ρ₂A₂V₂ czyli ρAV₌const. Jeśli płyn jest nieściśliwy to ρ₁=ρ₂ i równanie przyjmuje postać A₁V₁=A₂V₂ czyli AV=const. Iloczyn AV określa wielkość zwaną często strumieniem objętościowym lub też natężeniem przepływu z równania wynika, że prędkość jest odwrotnie proporcjonalna do pola przekroju i jest większa dla mniejszych przekrojów.(W sytuacji ogólniejszej gdy w strudze istnieją źródła lub ściegi oraz gdy gęstość płynu zmienia się w czasie i przestrzeni masa płynu też musi być zachowana. Możemy napisać równanie ciągłości wyrażające ten fakt ma ono postać ∂(ρVx)/∂x+∂(ρV_y)/∂y+∂(ρV_z)/∂z +∂ρ/∂t=S:Vx,Vy,Vz-składowe prędkości płynu:zarówno gestosci ρ

29. Rurka Pitota i zwężka VenturiegoZwężka (rurka) Venturiego jest to przyrząd wstawiany do rury z przepływająca cieczą w celu pomiaru jej prędkości przepływu. Ciecz o gęstości ro płynie przez rurę o przekroju A która w pewnym miejscu ulega zwężeniu do przekroju A i w tym miejscu dołącza się ramiona nanometr wypełnionego cieczą o gęstości ro' Stosując równanie Bernouliego i równanie ciągłości masy możemy napisać wzór na prędkość Natężenie prądu R=vA;v=a√(2(ρ'-ρ)gh/(ρ(A²-a²): RURKA PITOTA-służy do mierzenia predkości przepływu gazu Rozważamy gaz przepływający obok otworów w punktach A umieszczonych na tyle daleko aby prędkość i ciśnienie na zewnątrz otworów miały taki same wartości jak dla swobodnego strumienia gazu. W lewym ramieniu manometru ciśnienie jest statyczne p_a, a w punkcie B prędkość zostaje zredukowana do zera gaz jest nieruchomy. Ciśnienie p_b jest pełnym ciśnieniem uderzenia gazu :p_a+1/2ρv²=p_b, p_a+ρ'gh=p_b, 1/2ρv²=ρ'gh, v=√(2ρ'gh/ρ).( Jeśli h jest różnicą wysokości cieczy w ramionach manometru a ro' gęstością cieczy to p_a+ro'*gh=B )

30. Równanie BernouliegoRozważamy nie lepki ustalony nieściśliwy przepływ płynu przez rurę (RYS) skoncentrujemy naszą uwagę na tej części płynu która jest zakreskowana rozważmy ruch tej cz. płynu od położenia a do b . Siłami które wykonują pracę nad układem zakreskowanym są siły parcia p1A1, p2A2. Pracę W wykonywaną nad układem możemy znaleźć 1. Praca wykonywana nad układem przez siłę parcia p1A1 wynosi p1A1Δl₁ prze siłę parcia l2A2 wynosi to samo 3. Prace wykonana przez siłę grawitacyjną jest związanaz z podnoszeniem płynu z wysokości h1 na wys. h2 wynosi ona mg(h2-h1), czyli praca jest równa W=p1A1Δl₁-p2A2Δl₂-mg(h2-h1) a1Δl₁=a2Δl₂ a to jest objętość zakreskowanej powierzchni płynu, można zapisać jako m/ρ W=(p1-p2)m/ρ-mg(h2-h1). Zmiana en kinetycznej wynosi ΔK=1/2mv²₂-1/.2mv²₁ Z tw o pracy i en otrzymujemy W=ΔK, czyli (p1-p2)(m/ro)-mg(h2-h1)=1/2mv²₂-1/.2mv²₁ otrzymujemy p1+1/2ρv²₁+ρgh₁ =p2+1/21/2ρv²₂+ρgh₂ czyli p.+1/2ρv²+ρgh=const. Jest to równanie Bernouliego stosuje się je ściśle do przepływu ustalonego gdyż występujące w nim wielkości biegną wzdłuż osi rury

.31. Metody pomiaru ciśnienia statycznego i dynamicznegoStatyczne: barometr rtęciowy Torriciellego, manometr otwarty, aneroid, Dynamiczne:Zweżka Venturiego, rurka Pitota.

32. Drgania harmoniczne prosteW ruchu harmonicznym prostym siła działająca na ciało jest proporcjonalna do wychylenia z położenia równowagi i rest skierowana do pkt równowagi. Siła ta nosi nazwę siły sprężystej. Przyjmując, że ruch odbywa się wzdłuż osi x moźemy zapisać F = -k (x-x_o ), gdzie ka jest współczynnikiem proporcjonalności, xo - położeniem równowagi. Liniowa zależność między siłą i wychyleniem z położenia równowagi nosi nazwę prawa Hooka. Przyjmujemy że xo = 0. Wówczas F = - kx Ponieważ

więc równanie ruchu ciała o masie m. pod wpływem siły sprężystej będzie miało postać

Ruch opisany tym równaniem jest ruchem harmonicznym, a samo równanie nosi nazwę równania oscylatora harmonicznego. Rozwiązaniem jest funkcja

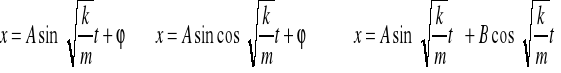
A, B, ϕ są pewnymi stałymi. A stała A występująca w równaniu oznacz maksymalne wychylenie z położenia równowagi, jest to amplituda drgań. Wyrażenie

okresla wychylenie w danej chwili czsu. Jest to faza drgań. ϕ jest fazą początkową okreslającą wychylenie w chwili t = 0 zarówno A jak i ϕ sa zadane przez warunki początkowe. Z równań wynika że x(t) jest okresową funkcją czsu tzn x(t) = x (t+T). Czs ten nazywamy okresem drgań. Po upływie czasu T faza zmienia się o 2π więc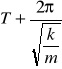

Odwrotnością okresu jest częstotliwość drgań υ. Jest to liczba drgań wykonywanych w jednostce czsu. Natomiast wielkość

nazywamy częstością kątową. Drgania, które odbywaja się pod wpływem tylko siły sprężystej nazywamy drganiami swobodnymi lub własnymi. Cęstość drgań własnych jest określona przez parametry samego oscylatora, tzn przez siłę sprężystości i masę układu.

Równanie oscylatora możemy zapisać

Prędkość i przyśpieszenie w ruchu harmonicznym otrzymamy różniczkując względem czsu równanie

Z równania wynika że współczynnikiem proporcjonalności między wychyleniem a przyspieszeniem jest kwadrat częstości drgań własnych.

(Drgania harmoniczne proste-ruch sinusoidalny ciała wywołany siła ,ruch bez tarcia. Równanie ruchu prostego oscylatora harmonicznego: d²x/df²+kx/m=0: rozwiązanie x=Acos(ωt+ϕ)

33. Drgania harmoniczne tłumione-ruch harm.prosty ,lecz ze względu na tarcie i opory ośrodka energia układu zmniejsza się co powoduje zmniejszenie amplitudy ruchu do zera.;

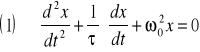
ω₀²=k/m jest kwadratem częstotliwosci dragań własnych τ = m/r - czas relaksacji, przyjmujemy iż β = 1/2τ gdzie β współczynnik tłumienia.Równanie (1) jest równaniem oscylatora harmonicznego tłumionego. Analizuje się trzy przypadki:

- przypadek periodyczny

- przypadek krytyczny

- przypadek aperiodyczny

Dla przypadku periodycznego rozwiazanie równania ma postać

gdzie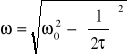

jest częstotliwością drgań tłumionych. Z wyrażenia (2) wynika, że amplituda drgań tłumionych maleje wykładniczo z upływem czasu.
Tłumienie zmniejsz także częstość drgań oscylatora, przy czym dla niezbyt dużych drgań można przyjąć, że ω≅ω₀. Z równania powyzszego wynika również, że im większy wsoółczynnik tłyumienia tym drgania szybciej zanikają. Wartością często charakteryzującą tłumieniae w ruchu harmonicznym jest logarytmiczny dekrement tłumienia Λ. Tłumienie oscylatora i w rezultacie zmniejszenie amplitudy drgań powoduje, że maleje także całkowita energia oscylatora

Szybkość zmiany energii oscylatora w czsie dE/dt = -(1/τ)EEnergia oscylatora tłumionego maleje wykładniczo z czsem. Jest to związane z tym, że oscylator wykonuje przce przeciwko sile oporu. Inną wielkością, która charakteryzuje oscylator jest współczynnik dobroci. Im oscylator jest słabiej tłumiony, tym jego dobroć jest większa.(Drgania harmoniczne tłumione-ruch harm.prosty ,lecz ze względu na tarcie i opory ośrodka energia układu zmniejsza się co powoduje zmniejszenie amplitudy ruchu do zera.; d²x/dt²+2Βdx/dt+ω_o²x=0;x=A_oe-^Βt(sinωt+ϕ):Β-stała tłumienia.)

34. drgania harmoniczne tłumione-ruch harmoniczny stale pobudzany zewnętrzną siłą harm o częstotliwości.ω i amplitudzie _o.;md²x/dt²+bdx/dt+mω_o²x=F_osin(ω₁t):d²x/dt²+2Βdx/dt+ω_o²x=γsin(ω₁t);x=Βsin(ω₁t+ϕ);γ=F_o/m.;ϕ-przesunięcie fazowe;Β-ampllituda.

34.DRGANIA HARMONICZNE WYMUSZONEW drganiach harmonicznych tłumionych, na skutek oporów ruchu, amplituda maleje wykładniczo w czasie, co powoduje ich zanikanie. Odmienna sytuacja powstaje wtedy, gdy na oscylator działa zewnętrzna siła okresowa. Jako przykład z praktyki można tu podać most drgający pod wpływem maszerującej przez niego kolumny wojska, czy widełki stroikowe (kamerton) wykonujące drgania gdy poddane są działaniu siły okresowej pochodzącej od fali głosowej. Drgania, które powstają ww takich zjawiskach nazywamy drganiami wymuszonymi. Drgania wymuszone mają taką częstość, z jaką działa siła zewnętrzna, a nie taką, jaka jest częstość własna ciała. Jednak reakcja ciała zależy od stosunku jaki zachodzi między częstością wymuszoną a częstością własną. Kolejne impulsy, nawet niewielkie, ale następujace w odpowiednich chwilach (zsynchronizowane), mogą doprowadzić do drgań o dużej amplitudzie.Równanie ruchu oscylatora (np. ciała o masie m zawieszonego na sprężynie o współczynniku sprężystości k, przy drganiach tłumionych siłami tarcia o wartościach proporcjonalnych do prędkości ruchu) o wymuszonej częstości drgań wynika z drugiej zasady dynamiki. W równaniu ruchu oprócz siły sprężystej (-kx) sprowadzającej ciało do położenia równowagi oraz siły tłumiącej -bdx/dt (gdzie b - współczynnik proporcjonalności) wystepuje jeszcze okresowa siła zewnętrzna F_mcosωt, gdzie F_m jest maksymalną wartością siły zewnętrznej a ω - jej częstoscią kołową.

Z równania F = ma otrzymuje się:

Rozwiązaniem tego równania jest całka

, gdzie
oraz
, a ponadto ω₀ -nietłummiona częstość własna układu.

Dla b=0 to znaczy, gdy nie występuje tłumienie, wartość wspólczynnika G zależy od różnicy częstości siły wymuszającej i częstości własnej układu. Jeżeli różnica ta jest duża to amplituda (F_m/G) powstałego ruchu jest mała. Z kolei, gdy częstość siły wymuszającej zbliża się do częstości własnej układu to amplituda powstałego ruchu dąży do nieskończoności. W układach rzeczywistych, zawsze występuje tłumienie, tak że amplituda drgań powstałego ruchu może mieć wartość bardzo dużą lecz skończoną. Częstość siły wymuszającej ω, przy której amplituda oscylacji osiąga maksimum nazywa się częstością rezonansową, a zjawisko - rezonansem. Im jest mniejsze tłumienie tym częstość rezonansowa jest bliższa częstości własnej układu nietłumionego. 35.RÓWNANIA RÓŻNICZKOWE OPISUJĄCE RÓŻNE RODZAJE DRGAŃSiła działająca proporcjonalnie do wychylenia x masy z położenia równowagi jest przeciwnie skierowana niż to wychylenie. Można napisać F = -kxMinus oznacza, że siła F i wychylenie x mają zwroty przeciwne. Ponieważ według II zasady Newtona F = ma można napisać ma = -kx. Dzieląc obie strony równanie przez m. i oznaczając iloraz k/m. przez ω² możemy napisać a = -ω²x. Równanie to wyraża zależność między przyśpieszeniem a i wychyleniem x. Przyśpieszenie w rozważanym ruchu jest proporcjonalne do wychylenia i ma znak przeciwny. Każde drganie mające taką własność nazywamy drganiem harmonicznym. Ponieważ przyspieszenie w ruchu prostoliniowym, jest drugą pochodną drogi względem czasu a = d²s/dt² zatem skoro drogę przebytą liczoną od punktu O oznaczyliśmy przez x, to możemy napisać a = d²x/dt². Podstawiając to wyrażenie za a otrzymamy d²x/dt² = -ω²x. Jest to równanie różniczkowe drgania harmonicznego. Rozwiązaniem tego równania jest x = Asin (ωt + ϕ ) gdzie A i ϕ są to pewne wielkości stałe, t - czas.W przypadku drgań, które często obserwójemy w przyrodzie, oprócz siły proporcjonalnej do wychylenuia działającej ku środkowi ruchu działa jeszcze siła hanująca ruch ( opór środowiska, tarcie wewnętrzne ). Można założyć, że siła hamująca jest proporcjonalna do prędkości ruchu drgającego i jest skierowana zawsze przeciwnie do chwilowej prędkości ruchu. Zatem na punkt wychylony o x z położenia równowagi będądziałały dwie siły, jedna proporcjonalna do wychylenia, druga do prędkości. Ozanaczając współczynniki proporcjonalności k₁ i k₂ można napisać F₁ = -k₁x F₂ = -k₂dx/dt. Opierając się na równaniu wyrażającym II zasadę Newtona można napisać

Dzieląc wszystkie wyrazy przez m. i przenosząc na lewą stronę otrzymujemy

Wprowadzjąc oznaczenia k₂/m. = a oraz k₁/m. = ω₀² otrzymamy

Jest to równanie różniczkowe drgań tłumionych. Rozwiązaniem tego równania jest

gdzie A jest stałą od której zależy pierwsze, największe wychylenie.

Ważnym przypadkiem jest przypadek ruchu pkt, który może drgać ruchem harmonicznym gdy nań działa periodyczna siła zewnętrzna F = F₀sinω₁t. Dodając diałanie tej siły do sił działających w poprzednim przypadku i pisząc II zasadę Newtona dla tego przypadku otrzymamy

Dzieląc całe równanie przez m. i oznaczjąc k₂/m= a, k₁/m. = ω₀² oraz F₀/m. = A otrzymamy równanie drgania wymuszonego

Rozwiązaniem tego równania będzie x = Csin (ω₁t - ϕ )

36. Rezonans mechaniczny-są to drgania wzmożone o częstotliwości bliskiej lub równej częstotliwości drgań własnych układu drgającego

.37.Dobroć Układu drgającego;

Jest to wielkość charakteryzujące oscylator, zdefiniowana jako iloczyn 2π i stosuku enerii zmagazynowanej do energii traconej w jednym okresie. Im oscylator jest słabiej tłumiony, tym jego dobroć jest większa.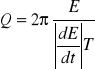

Q=π/Ω=πN_e=π/(ΒT)=πιν=ιω/2;Ω-log.dekr.tłumienia;N_e-liczba drgań w czasie relaksacji ;ι-czas relaksacji.: Q=ω_rel/(Δω);Β_rel/x_o=(F_omω_o²)/(m²Βω_oF_o)=ω_o/2Β=2π/T=π/Ω=Q

Dobroć Układu drgającego;Q=π/Ω=πN_e=π/(ΒT)=πιν=ιω/2;Ω-log.dekr.tłumienia;N_e-liczba drgań w czasie relaksacji ;ι-czas relaksacji.: Q=ω_rel/(Δω);Β_rel/x_o=(F_omω_o²)/(m²Βω_oF_o)=ω_o/2Β=2π/T=π/Ω=Q

38.Zasada zachowania energii w ruchu harmonicznym prostym

Energia mechaniczna oscylatora harmonicznego jest równa energii kinetycznej i energii potencjalnej sił sprężystych. Energia kinetyczna

natomiast energia potencjalna

Zatem energia całkowita

Ponieważ ω²=k/m. , więc całkowitą enerię oscylatora możemy przedstawić w postaci

Całkowita energia oscylatora jest stała i proporcjonalna do kwadratu amplitudy. Chwilowe wartości energii potencjalnej i kinetycznej są natomiast funkcjami czasu. Energia potencjalna jest najwieksza, gdy ciało znajduje się w skrajnych położeniach, a równa zero gdy ciało przechodzi przez położenie równowagi. Energia kinetyczna natomiast odwrotnie: jest równz zeru w skrajnych położeniach, a największ przy przechodzeniu przez położenie równowagi. Jednak średnie wartości tych energii w czasie są sobie równe.(Zasada zachowania energii-Energia może byc przekształcona z jednej formy w inną,ale nie może być stworzona ani zniszczona,energia całkowita jest wielkością stałą.)39.E=1/2kx²+1/2mv²;E=1/2mω_o²A_o²e^-2Βt;dE/dt=-2Β(1/2mω_o²A_o²e^-2Βt)=-2ΒE;-dE=2ΒEdt;-ΔE=2ΒET;-ΔE/E=2ΒT=2Ω=2π/Q-względna zmiana energii w czasie okresu.

41. SKŁADANIE DRGAŃ RÓWNOLEGŁYCHPrzy drganiach dowolnych punktu, wychylenie wypadkowe w dowolnej chwili, można określić jako sumę wektorów wychyleń drgań składowych. Obowiązuje tu zasada superpozycji. Sumowanie takie upraszcza się znacznie przy składaniu drgań równoległych. Wtedy sumę geometryczną można zastąpić sumą algebraliczną z uwzględnieniem znaków “+” i “-” dla wychyleń po obu stronach położenia równowagi. W wyniku składania dwóch drgań harmonicznych równoległych o jednakowych pulsacjach powstaje ruch wypadkowy również harmoniczny (ze zmienioną amplitudą), dla którego wykresem zależności wychylenia od czasu jest sinusoida. Jeżeli jednak pulsacje obu ruchów składowych nie są jednakowe, to ruch wypadkowy nie jest już ruchem harmonicznym, a jego wykresem nie jest już sinusoida lecz krzywa bardziej skomplikowana.Omówioną zmiane charakteru drgań złożonych można przedstawić doświadczalnie w następujący sposób.Z lejka odpowiednio zawieszonego i wprawionego w ruch wahadłowy wysypuje się piasek na papier przesuwający się ruchem jednostajnym w płaszczyźnie poziomej - rys. a. W przybliżeniu sinusoidalny rozkład piasku na papierze przedstawia obraz wychyleń wylotu lejka od płaszczyzny równowagi w funkcji czasu.

Jeżeli jednak przez zawieszenie dodatkowego obciążenia zmienimy układ drgający tak, że lejek będzie równoczesnie uczestniczył w dwóch ruchach drgających (własnym i układu złożonego w całość) o różnych okresach, to ślad jaki zostawi piasek na papierze nie będzie już sinusoidą. Lejek będzie wykonywał drgania okresowe lecz nie będą to drgania harmoniczne.

42 SKŁADANIE DRGAŃ WZAJEMNIE PROSTOPADŁYCH.Układ zdolny do wykonywania drgań może jednoczesnie wykonywać dwa lub więcej drgań. W takim przypadku wykonuje on drganie wypadkowe, będące wynikiem poszczególnych drgań składowych. Wp rzypadku gdy kierunki obydwu drgań składowych tworzą ze sobą kąt prosty poszczególne wychylenia dodajemy geometrycznie (wektorowo).y₁ - wychylenie spowodowane drganiem I, y₂ - wychylenia spowodowane drganiem II, y - wychylenie wypadkowe, A₁, γ_1, t₁ - amplituda ,częstość, czas I

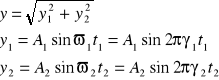
Czas liczymy w każdym przypadku od pierwszego przejścia przez położenie równowagi w określoną stronę. Jeżeli połączymy pkt charakteryzujące poszczególne wartości wychylenia wypadkowego, otrzymamy rodzinę lini, które nazywamy krzywymi Lissajous.

Warunki	wynik nakładania
γ1=γ2, A1 = A2, Δϕ=0	linia prosta
γ1=γ2, A1 = A2, Δϕ=π/2	okrąg
γ1=γ2, A1 ≠ A2, Δϕ=π/2	elipsa

43 Czas relaksacji i logarytmiczny dekrement tłumienia.

Wielkością, którą częstao charakteryzujemy tłumienie w ruchu harmonicznym jest logarytmiczny dekrement tłumienia Λ. Jest to logarytm naturalny ze stosunku amplitud dwóch kolejnychyleń w tę samą stronę, tzn następujących po sobie w odstępie czsu równym okresowi drgań.

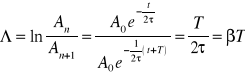
Energia oscylatora tłumionego maleje wykładniczo z czasem. Jest to z wiązane z tym, że oscylator wykonuje pracę przeciwko sile oporu. Możemy napisać interpretację fizyczną stałej τ. Jest to czas po mupływie którego energia oscylatora emniejsz się e - krotnie. Czas ten nazywamy czsem relaksacji τ =1/β.

44 PODSTAWOWE PARAMETRY OPISUJĄCE FALĘ.

- równanie falowe,Φ = Φ(x,y,z,t)Φ - wielkość charakteryzująca stan zaburzenia ośrodka, zależna od położenia i czasu. W przypadku propagacji fali w cieczty lub gazie opisuje zmianę gestaości lub ciśnienia osrodka spowodowaną przejsciem fali. W przypadku ciał stałych będzie przemieszczeniem atomów z położenia równowagi,- częstotliwość ω i amplituda drgań Φ₀ ,- predkość rozchodzenia się fali ( propagacji ), ściślej predkość przemieszcznia się określonej fazy fali, czyli prędkość fazowa v, - okres T,

- długość fali λ odległość na jaką przemieści się zaburzenie w czsie jednego okresu λ = vT,

- liczba falowa k, liczba długosci fali przypadająca na jednostkę dlugosci pomnozona przez 2π k=2π/λ.Postawiając te wielkości do równania falowego otrzymujemy równanie postaci Φ = Φ₀ sin (ωt - kx).

45 RÓWNANIE FALOWE POSTAĆ JEGO ROZWIĄZAŃ.Różniczkując którekolwiek z równań fali, np.:

dwa razy względem t i dwa razy względem x . Otrzymamy wtedy

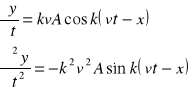
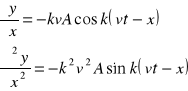
Porównując powyższe równania możemy napisać:

(1)

Jest to równanie różniczkowe fali płaskiej. Jak można wykazać jest ono o wiele ogólniejsze od równania

Równanie to spełniają nie tylko fale biegnące w dodatnim i ujemnym kierunku osi x lecz i fale poprzeczne i podłuzne można wykazać, że każdy ruch podlegający temu równaniu jest ruchem falowym. Ruch falowy dany przez równanie

jest pewnym szczególnym ruchem falowym. Jest to fala harmoniczna płaska. Wszystkie cząstki środowiska drgają w niej ruchem harmonicznym. Można wykazać, że równanie (1) przedstawia nie tylko falę harmoniczną, lecz rozchodzenie się jakiegokolwiek zaburzenia w środowisku sprężystym.

46. PODZIAŁ FAL WEDŁUG RÓŻNYCH KRYTERIÓWW zależności od kierunku drgania cząstek względem kierunku rozchodzenia się fali rozróżniamy pale podłużne i poprzeczne. W przypadku fal podłużnych cząstki drgają w kierunku rozchodzenia się fali. Fale podłużne mogą rozchodzić się zarówno w ośrodkach ciekłych, jak i w ciałach stałych. Dla fal poprzecznych kierunek drgań cząstek jest prostopadły do kierunku rozchodzenia się fali. Fale poprzeczne mogą rozchodzić się tylko w ciałach stałych. Wyjątek stanowią tzw. Fale powierzchniowe, które mogą rozchodzić się na powierzchni cieczy np. fale na wodzie.Ze względu na kształt rozróżniamy: - fale kołowe, np. na powierzchni wody na około miejsca wrzucenia kamienia, - fale kuliste, np. fale głosowe na około drgającego dzwonka, - fale płaskie np. fala wywołana przez drgającą płaszczyznę lub fale głosowe rozchodzące się w rurach - fale walcowe, carakteryzuje się tym, że powierzchnie walcowe są walcami o wspólnej osi. Źródłem takiej fali może być pulsujący cienki pręt.W zależności od liczby wymiarów niezbędnych do opisu kierunku rozchodzenia się energii możemy rozróżnić fale jedno-, dwu-, i trójwymiarowe. Fale biegnące wzdłuż linii czy sznura są jednowymiarowe. Fale powierzchniowe lub zmarszczki na wodzie wywołane np. wrzuceniem kamienia są dwuwymiarowe. Fale dźwiękowe oraz fale świetlne wybiegające radialnie z małego ośrodka są trójwymiarowe.Dźwięk, promieniowanie, światło polegają na rozchodzeniu się ruchu falowego Gdy zmusimy cząsteczkę A znajdującą się na powierzchni jednorodnej cieczy do drgania harmonicznego to i sasiednie cząsteczki zaczynają drgać i po powierzchni cieczy od cząstki A biegnie fala w postaci kół, których środkiem jest cząstka A. Punkty które posiadają jednakowe fazy drgania, leżą na obwodzie koła zatoczonego dookoła cząstki A. Okrąg tego koła nazywamy linią jednakowej fazy drgania lub linia fazowa. Linie fazowe będą w tym przypadku okręgami kół. Jeżeli wewnątrz gazu lub cieczy w pewnym punkcie będziemy wykonywać periodyczne zagęszczenie i rozrzedzenie , to te zmiany gęstości będą się rozchodzić w postaci fal kulistych na wszystkie strony. Jeżeli w pewnej chwili poprowadzimy powierzchnie przez wszystkie punkty o takiej samej fazie, to będzie ona powierzchnią kulista. Fale taką nazywamy kulistą, a powierzchnie kuli przechodzącej przez wszystkie pkt o tej samej fazie drgania - powierzchnia fazową. Jeżeli powierzchnie fazowe są płaszczyznami to fale nazywamy falą płaską. Możemy wywołać falę płaską np. pobudzając powierzchnie wody do drgania za pomocą długiej deski lub belki.47 Prędkość propagacji fali akustycznej w ośrodku gazowym i ciele stałym, należność prędkości fali w gazach od ciśnienia i temperatury.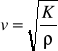

K - moduł ściśliwości

Wzór ten określa prędkość propagacji fal sprężystych w gazach i cieczach. W ośrodkach tych propaguje się tylko fala podłużna. W procesie propagacji fali ruchy cząsteczek zachodzą szybko, nie ma wymiany ciepła między różnymi elementami ośrodka i dlatego proces ten jest adiabatyczny. Dlatego też moduł sciśliwości występujący w (1) ma prędkość propagacji fali. Jest adiabatycznym modułem ściśliwości. Dla gazów doskonałych moduł ten jest równy χp. Dlatego predkość propagacji fali jest równa

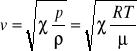
stała gazowa, T - temperatura bezwzględna, μ - masa jednego mola gazu, χ - stała równa stosunkowi ciepła właściwego gazu przy stałum ciśnieniu do ciepła właściwego w stałej objętości.Zmiana ciśnienia wywołuje zmianę gęstosci, jednak nie wpływa na prędkość.

Podobnie wyznaczamy predkość w ciałach stałych . Prędkość propagacji fali podłużnej V_L i poprzecznej V_T w izotopowych ciałach stzłych wynosi odpowiednio

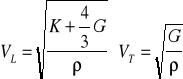
E - moduł Younga, μ - współcz. Poissona, G - moduł sprężystości postaci. Prędkość fal podłużnych jest większa niż fal poprzecznych.

48-52 Fala stojąca Jeżeli w ośrodku rozchodzi się kilka fal , to drgania cząstek ośrodka stanowią geometryczną sumę drgań, które wykonałyby cząstki podczas rozchodzenia się każdej osobno. Fale po prostu nakładają się nie zaburzając się wzajemnie .Stwierdzenie to nosi nazwę zasady superpozycji fal. W przypadku gdy drgania wywołane oddzielnymi falami w każdym z punktów ośrodka mają stałą różnice faz, fale nazywa się spójnymi lub koherentnymi. Podczas składania fal spójnych powstaje zjawisko interferencji. Polega ono na tym że drgania w pewnych punktach ulegają wzmocnieniu , a w innych osłabiają się wzajemnie. Bardzo ważny przypadek interferencji ma miejsce podczas nakładania się dwóch dal o jednakowej amplitudzie, rozchodzących się w przeciwnych kierunkach . Powstający w wyniku tego proces nazywamy falą stojącą. Praktycznie fale stojące powstają podczas odbijania się fali na przeszkodach. Falę stojącą daje wówczas nałożenie się fali padającej na przeszkodę i fali odbitej. Weźmy równania dwóch fali f₁(r,t)= A₀sin (ωt- kr₁) oraz f₂(r,t)= A₀sin(ωt-kr₁-2kr+d); ogólnie f(r,t)=f₁(r,t)+f₂(r,t), czyli mamy f(r,t)= A₀[sin(ωt-kr₁)+sin(ωt-kr₁-2kr+d), z tego f(r,t)=2A₀[sin(ωt-kr₁-kr+d/2)cos(kr-d/2)] i ostatecznie f(r,t)=2A₀cos(kr-d/2) sin(ωt-kl+d/2) (do sinusa to amplituda fali stojącej reszta to faza l=r₁+r , a d- skok fazy); Przy odbiciu od ośrodka gęstszego d=*, a od ośrodka rzadszego d=0.Dla gęstszego węzły cos(kr-d/2)=0, czyli kr-*/2=(2n-1)*/2, z tego r=nλ/2 ,gdzie λ=2π/k Gęstszy strzałki cos(kr-π/2)=1; kr-π/2=nπ; podstawiamy za k=2π/λ , czyli r=(2n+1)λ/4 n=1,2,3...Dla ośrodka rzadszego węzły d=0 coskr=0; kr=(2n+1)π/2; r=(2n+1)λ/4 ; strzałki coskr=1; kr=nπ

53 Natężenie mierzy się ilością energii przenoszonej w jednostce czasu przez jednostkę powierzchni ustawionej prostopadle do promienia fali. Natężenie wyraża się w W/m². Ponieważ natężenie dźwięku jest proporcjonalne do ilości energii , a en. do kwadratu amplitudy, więc tym samym obowiązuje proporcjonalność natężenia do kwadratu amplitudy drgań źródła. I=wc (gdzie w-średnia wartość objętościowa energii)53,54,55 Poziom natężenia słyszalność człowieka I₀=10^-12[W/m²] do 1[W/m²] ,L=0 do 120dB ; L_I =log I/I₀ [B] lub L=10 log I/ I₀ I₀ - poziom odniesienia= 10^-12[W/m²] ; I= p₀²/ 2ρ₀c ; Dla fali sinusoidalnej p₀²/2= p² (z daszkiem) L_p =20log p/ p_odn. p_odn. 2*10^-5 [N/m²] Dla fali płaskiej L_I = L_pAddytywność poziomu ciśnienia L₁ L₂ ; I= I₁+ I₂ ; p²=p²₁+p²₂ ; L₂=10log I₂/I₀=20logp/p_odn czyli jeżeli np. różnica poziomów ciśnienia akustycznego ( p. nztęż.) wynosi 40 dB to znaczy to , że dźwięk ma natężenie 10⁴ razy mniejsze , a ciśnienie akustyczne 10² razy mniejsze niż dźwięk pierwszy. I₁=I_o log^L1/10 I₂=I_o log^L2/10 ogólnie L=10log ∑ (od i=1 do n) 10^Li/10

Impedancja ( ogólnie z= p.(_r,t)/u(r,t) ; z=z e^iϕ ) dla fali płaskiej z=ρ₀c ρ₀c-oporność akustyczna ośrodka, jest liczbą rzeczywistą nie ma przesunięcia fazowego; Dla fali kulistej p(r,t)=1/r f(t-r/2); p(r,t)=A/r sin(ωt-kr); r>10λ. Natężenie fali akustycznej Energia akustyczna przypadająca na jednostkę powierzchni w jednostce czasu (wartość średnia w czasie) I(r) =<p(r,t)u(r,t)> jeżeli p(r,t)=p₀ sin(ωt-kr); p.(r,t) / u(r,t)= ρ₀c → u(r,t)=p.(r,t)/ ρ₀c I(r)=1/ρ₀c <p²(v,t)> - dla fali płaskiej I(v)=1/T₀^T p.(r,t)u(r,t) dt ; I=wc dla fali płaskiej w=dE/dV

56(53). Podstawowe cechy dźwięku Każdy dźwięk charakteryzują następujące cechy wysokość, natężenie, barwa. Fizyczną miarą wysokości dźwięku jest częstość drgań źródła dźwięku .Dźwięk jest tym wyższy im większa jest częstotliwość n , i odwrotnie. Częstość jednego drgania na sekundę nazywamy hercem (Hz), granice słyszalności wynoszą n=16 do 20 000 Hz. (pies 38kHz wieloryb 100kHz) W muzyce wysokość dźwięku wyraża się w umownie przyjętej skali zawierającej 8 części OKTAW, odpowiadającym częstością od 16 do 4096 Hz. Natężenie dźwięku jest cechą odróżniającą dźwięki silne od słabych. Fizyczną miarą natężenia dźwięku jest natężenie fali dźwiękowej w danym punkcie I=(2π²v)dr²n² ze wzoru wynika ,że natężenie dźwięku jest wprost proporcjonalne do gęstości ośrodka , kwadratu amplitudy i kwadratu częstości drgań. Dźwięki jednakowej wysokości i o jednakowym natężeniu wydawane przez różne źródła różnią się od siebie. Różnice te są spowodowane charakterem drgań źródła (najczęściej nie są to drgania harmoniczne lecz złożone w skutek interferencji fal poszczególnych elementów drgających źródła) i określają barwę dźwięku. Wykreślając za pomocą fonografu linie falowe, odpowiadające różnym źródłom drgań, można się przekonać , że barwa dźwięku zależy od kształtu linii falowej. Ustalając liczbę występujących w danym dźwięku tonów harmonicznych i stosunki ich natężeń otrzymujemy charakterystykę danego dźwięku w postaci widma akustycznego Głośność- jest to wielkość subiektywna zależna od oceny siły wrażenia słuchowego wywołanego tą falą. Głośność dźwięku zależy nie tylko od jego średniej kwadratowej ciśnienia, lecz również od czułości ucha, która jest różna dla dźwięków o różnych natężeniach i częstościach. Np. jeżeli ciśnienie akustyczne jest mniejsze od pewnej wielkości p₀ ( progu słyszalności) to dźwięk taki nie będzie słyszalny. Próg słyszalności zależy od częstości dźwięku, osiągając najmniejszą wartość rzędu 2*10^-5 N/m² dla częstotliwości 1500-3000Hz. W celu porównania głośności dźwięku o różnych częstotliwościach wprowadza się pojęcie poziomu głośności. Wielkość ta równa jest liczbowo odliczonemu od umownego zera poziomu ciśnienia akustycznego słyszanego tak samo głośno jak dźwięk wyjściowy, którego częstość równa się 1000Hz. Umowne zero poziomu ciśnienia akustycznego przyjęto jako równe 2*10^-5 N/m². Poziom głośności dźwięku mierzy się w fonach ( poziom głośności dźwięku jest równy jednemu fonowi jeżeli poziom ciś. akust. , tak samo słyszanego dźwięku wzorcowego równa się 1 dB.Fale sprężyste wzbudzane istniejącymi źródłami dźwięku są połączeniem fal sinusoidalnych i (tony proste lub czyste) o różnych częstotliwościach i amplitudach. W zależności od obrazu WIDMA można je podzielić na 2 gr. Pierwsza to dżwięki tonalne ( posiadają widmo liniowe ), drugie to szumy posiadają ona złożone widmo liniowe szum biały to szum o widmie ciągłym szum barwny ciągłe widmo w pewnym paśmie częstotliwości

.60 Prawo Fechnera - Webera aby ocenić intensywność natężenia dźwięku ( donośność ) opieramy się na psychofizycznym prawie F.W. Zgodnie z tym prawem zmiana intensywności wrażenia jest proporcjonalna do log stosunku en. podrażnienia wywołujących wrażenia porównywane na podstawie tego prawa ustalono skalę poziomów subiektywnego natężenia dźwięku. Przyjęcie poziomu leżącego na progu słyszalności I₀ za poziom zerowy jest zrozumiałe. Umówiono się uważać za poziom zerowy taki poziom którego I₀ =10^-9 [erg/cm²s]. Jest to poziom trochę niższy od progu słyszalności przy 1000Hz. Wobec tego zgodnie z prawem F.W donośność dźwięku Ω jest proporcjonalna do log stosunku jego natężenia I do natężenia tego samego dźwieku na progu słyszalności Io. Ω= k log I/Io k- współczynnik proporcjonalności. Wielkość Ω nazywa się poziomem siły dźwięku. Zakładając k=1, wybieramy tym samym jednostkę miary poziomu dźwięku. Jednostka ta nazywa się belem [B]. Wobec tego Ω=log I/Io [Beli] używa się również jednostek 10* mniejszych zwanych decybelami [dB]. Wobec tego Ω=10logI/Io [dB].

61 Krzywa czułości ucha ludzkiego. Aby fala dźwiękowa mogła wywoływać wrażenie dźwięku natężenie dźwięku musi być większe od pewnej minimalnej wielkości zwanej progiem słyszalności. Dźwięk o natężeniu leżącym poniżej progu słyszalności jest zbyt słaby aby ucho mogło go przyjąć próg słyszalności zmienia się wraz z częstością. Ucho ludzkie jest najczulsze na drgania o częstościach leżących w obszarze 1000-3000 Hz. Próg słyszalności w tym obszarze dochodzi do wartości rzędu 10^-8 [erg/cm²s]. Ucho jest znacznie mniej czułe na dźwięki o częstościach wyższych i niższych. Ucho nie odbiera żadnych drgań jako drgań dźwiękowych jeżeli mają one częstosci mniejsze od 20 Hz i wyższe od 20000 Hz. Drgań o bardzo dużej mocy ucho ludzkie nie przyjmuje jako drgań dźwiękowych , wywołują one w uchu przykre wrażenie ucisku , które później przechodzi we wrażenie bólu. Max natężenie dźwięku po którego przekroczeniu powstaje przykre wrażenie bólu, nazywa się progiem odczuwania lub progiem wrażenia bólu . Próg wrażenia bólu różni się trochę dla różnych częstości. Między progiem słyszalności i progiem bólu znajduje się obszar słyszalności.

62 Infradźwięki i ultradźwięki, dźwiękiem w fizyce nazywamy dowolne fale sprężyste przy czym w odróżnieniu od słyszalnych fale o częstościach mniejszych od 16 Hz nazywamy infradźwiękami (poddźwiękami), a fale o częstościach przewyższających 20 kHz ultradźwiękami (naddźwiękami). Fale ultradźwiękowe o częstościach rzędu 10^6 Hz i wyższych nazywamy hiperdźwiękami. Górna granica częstości fal ultradźwiękowych odpowiada częstością przy których długości tych fal są porównywalne z odległościami międzycząsteczkowymi fale ultradźwiękowe posiadają szereg specyficznych własności jedną z nich jest fakt , że mogą one być podobne jak światło wysyłane w postaci wąskich ukierunkowanych wiązek zwanych promieniami ultradźwiękowymi własność ta wynika z małej dł. fali ultradzw. Ultradźwięki można zastosować do wykrywania wewnętrznych defektów (pęcherzy, pęknięć , niejednorodnych ) ciał stałych, a także określenia pojemności cieplnej substancji, wyznaczenia stałych sprężystości i lepkości substancji.

73 Widmo fal elektromagnetycznych Jednym z wniosków wypływającym z rozważań teoretycznych Maxwella było ustalenie, że zarówno pole elektryczne , jak i pole magnetyczne rozchodzą się z prędkością c równą c=1/ pierw. (εμ)gdzie εμ oznaczają odpowiednio przenikalność elektryczną i magnetyczną w próżni. Po podstawieniu do tego wzoru wartości εμ okazuje się, że prędkość rozchodzenia fali elektromagnetycznej w próżni jest stała , niezależna od częstotliwości i równa prędkości rozchodzenia s ie światła w próżni . Obecnie wiadomo, że p.e. wypełnia w sposób ciągły bardzo szeroki zakres częstotliwości. Ze względu na różne rodzaje stosowanych generatorów i detektorów w różnych przedziałach częstotliwości wprowadzamy pojęcie widma elektromagnetycznego uwzględniające podział p.e na różne rodzaje ( trzeba jednak pamiętać , że nie ma żadnych wyraźnych granic pomiędzy poszczególnymi rodzajami w. Przegląd w.e. zaczniemy od fal najdłuższych ,a więc o najmniejszych częstotliwościach . Są nimi najdłuższe fale radiowe o dugościach fal sięgających kilku kilometrów a cz. 150 Hz ,f. Średnie (setki metrów ) , krótkie (dziesiątki metrów) i ultrakrótkie (metry , decymetry). Za f. Radiowymi rozciąga się obszar mikrofal sięgający do długości fal rzędu 10^-3m. Warto wspomnieć o szerokim zakresie fal decy. i centymetrowych w radiolokacji i telewizji. Najkrótsze mikrofale nakładają się na najdłuższe fale zakresu podczerwieni , tzn. Zakres promieniowania cieplnego rozciągający się aż do długofalowej granicy promieniowania tzw. widma promieniowania widzialnego ( jest on bardzo wąski dł. fal od 7.6*10^-7m. do 4*10^-7m.). Od strony krótkich fal obszar widzialny graniczy z tzw. nadfioletem ( ultrafiolet ) sięgający do dł. f. rzędu 10^-8 m. Tutaj zaczyna się promieniowanie rentgenowskie pokrywające się z promieniowaniem gamma rozciągającym się do długości fal rzędu 10^-13 -10^-14 Należy tu podkreślić , że wszystkie te fale mają taką samą naturę, rozchodzą się w próżni z tą samą prędkością c, różnią się natomiast częstotliwościami i długościami fal .

1

---