TEMAT:
Przestrzeń metryczna

 

DEFINICJA 8.1    (DEFINICJA METRYKI)

 

           
           określmy funkcję

    taką, że

 ^{-  warunek nieujemności}

  -  warunek symetrii

  -  warunek nierówności trójkąta

Jeżeli d spełnia warunki 1^o - 4^o to mówimy , że d jest metryką, gdy są spełnione tylko 3

pierwsze warunki to d jest półmetryką.

Parę uporządkowaną (X,d) nazywamy zaś przestrzenią metryczną.

 

 

 

PRZYKŁAD 8.1    (PRZYKŁADY METRYK)

 

I.          Niech

                       

Udowodnimy, że tak zdefiniowana funkcja spełnia założenia metryki.  

 

Dowód:

Własności 1^o, 2^o i 4^owynikają bezpośrednio z własności bezwzględnej wartości.

Udowodnimy punkt 3^o. Z definicji mamy:

                               
  

c.n.u.

 

II.         Niech

                        oraz

 

            a)        
  jest to odległość euklidesowa

 

 

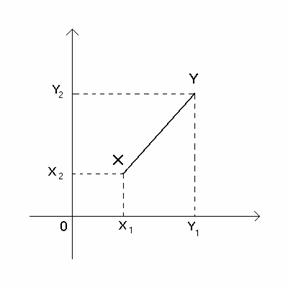
Dowód:

Warunki 1^o 2^o i 4^o są oczywiste, udowodnimy tylko warunek 3^o definicji 8.1.

W dowodzie będziemy korzystali z nierówności  Cauchy'ego.

 

 

 

 

 

 

 

 

 

            ale z nierówności Cauchyego wiemy, że:

 

            Zatem

c.k.d.

 

            b)

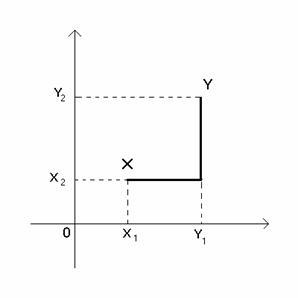
Niech
 - jest to tak zwana odległość taksówkowa.

 

 

 

Dowód:

Dowody warunków 1^o, 2^o i 4^o są oczywiste, udowodnimy zatem tylko warunek 3^o definicji metryki.

 

 

            c)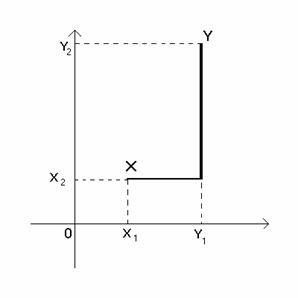
        
- jest to odległość maksimum.

 

Dowód:

Dowody warunków 1^o, 2^o i 4^o są oczywiste, udowodnimy

zatem tylko warunek 3^o definicji metryki.

 

 

 

 

 

 

 

 

 

 

 

 

III.        Niech

                                   wtedy

 

            ^{a)       
  - jest to odległość euklidesowa}

            ^{b)       
  - odległość taksówkowa}

            ^{c)        
  - odległość maksimum}

 

 

Dowody są analogiczne jak w przypadku II.

 

IV.       Niech X będzie dowolnym  zbiorem, takim że

 

Skonstruujmy funkcję d taką, że
 

    
wówczas d nazywamy metryką dyskretną.
 

Udowodnimy, że tak podana funkcja spełnia warunki metryki.

 

Dowód:

Warunki 1^o, 2^o i 4^o definicji 8.1. są natychmiastowe z określenia funkcji.

Zajmiemy się zatem warunkiem 3^o.

 Jeżeli: 
                        a) 
  to 
 

b) 
  to 

c) 
  to 

d) 
  to 

e) 
  to 

Tym samym pokazałem, iż w metryce dyskretnej  warunek 3^o  definicji metryki  jest zawsze spełniony.

 

 

 

 

PRZYKŁAD 8.2    (METRYKA W ILOCZYNIE KARTEZJAŃSKIM DWÓCH
                                      PRZESTRZENI METRYCZNYCH)

 

Niech
 będą przestrzeniami metrycznymi.

Niech:

            a)       
, 

           gdzie

           Jest to odległość euklidesowa w iloczynie kartezjańskim.

 

          b)      
- odległość taksówkowa w iloczynie kartezjańskim.

 

          c)      
- odległość maksimum w iloczynie kartezjańskim

 

 

            W dalszej części wykładu dana jest  przestrzeń metryczna
.

 

 

 

DEFINICJA 8.2     ( KULA OTWARTA)

 

            Niech 

           

 

 

 

PRZYKŁAD 8.3   

 
            Szukamy kuli
.

          I       

II     

 

            a) Kula w metryce euklidesowej              

           

        

             b) Kula w metryce taksówkowej

 

 

           Narysujmy wykres

         

            c) Kula w metryce maksimum

 

                         

 

         

 

 

DEFINICJA 8.3     (ZBIÓR OGRANICZONY)

 

Niech
powiemy, że: 
               

 

 

 

DEFINICJA 8.4     (ZBIÓR OTWARTY W PRZESTRZENI METRYCZNEJ)

 

           

 

 

TWIERDZENIE 8.1    (TOPOLOGIA W PRZESTRZENI METRYCZNEJ - czytaj: własności
                                                 zbiorów otwartych  w przestrzeni metrycznej)

 

            Niech

                     

                       (połączenie dowolnej ilości zbiorów otwartych jest zbiorem otwartym)
 

 
                  (przecięcie skończonej ilości zbiorów otwartych jest zbiorem otwartym)

           

            Uwaga.

Rodzinę podzbiorów z danego zbioru spełniającą warunki 1^o - 3^o nazywamy topologią.

Rodzina zbiorów otwartych przestrzeni metrycznej jest topologią i nazywamy ją

topologią indukowaną przez metrykę d.

 

 

 

Dowód:

 

  ( z definicji)

                                        
  ( bo X zawiera wszystkie „swoje” kule).

           

wystarczy przyjąć

 

 

 

TWIERDZENIE 8.2

 

            Kula otwarta jest zbiorem otwartym.

           

 

           

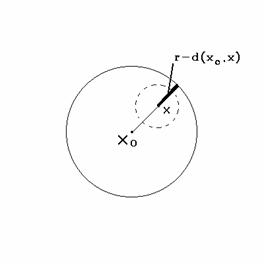
            Niech   

 

Dowód:

            Niech 

^Niech

Pokażemy, że

 

Niech

 Wtedy z (*) mamy
, ale z 3^o warunku definicji mamy:
 

_, 
a 
_, gdyż

 

Pokazaliśmy, że
,  a to oznacza, że
 

 

 

 

 

WNIOSEK:                 

 

               

 

 

 

DEFINICJA 8.5     (WNĘTRZE ZBIORU)

           

Niech
, 

i int A oznacza wnętrze zbioru A,

int A jest to największy zbiór otwarty zawarty w A .

 

 

 

WNIOSEK:

            ^{Jeżeli
   jest rodziną wszystkich zbiorów otwartych zawartych w A, to} 

            

 

 

 

DEFINICJA 8.6     (OTOCZENIE PUNKTU W PRZESTRZENI METRYCZNEJ)

 

           

Otoczenie punktu x_o nazywamy dowolny zbiór otwarty zawierający punkt x_o.

 

 

Uwaga.

W naszych rozważaniach będziemy stosować tylko otoczenia kuliste.

 

 

 

DEFINICJA 8.7     (ZBIORY DOMKNIĘTE)

 

Niech

 

 

 

TWIERDZENIE 8.3    (WŁASNOŚCI ZBIORÓW DOMKNIĘTYCH)

 

 

(przecięcie dowolnej ilości zbiorów domkniętych jest zbiorem domkniętym).

 (połączenie skończonej ilości zbiorów domkniętych jest zbiorem domkniętym).

 

Dowód.

Ad.

1^o            

              

                             

 

Ad.

2^o           

            
             

           Ad.

3^o

           

           

 

            Uwaga.

Kula domknięta jest zbiorem domkniętym.

 

 

 

DEFINICJA 8.8     (DOMKNIĘCIE ZBIORU)

           

            Domknięciem zbioru A nazywamy najmniejszy zbiór domknięty obejmujący zbiór A.

Domknięcie zbioru A będziemy oznaczać przez
.

 

 

 

WNIOSEK:

           

            Jeżeli
jest rodziną zbiorów domkniętych zawartych w X  i
, to

 

 

 

 

DEFINICJA 8.9     (BRZEG ZBIORU)

 

            Niech
,  

gdzie
 - oznacza brzeg zbioru A.

 

 

 

 

DEFINICJA 8.10      (GRANICA CIĄGU)

 

            Niech
 - będzie przestrzenią metryczną

           

             inaczej:

                

 

 

PRZYKŁAD 8.4

 

           

Sprawdzić czy ciąg
  jest zbieżny do g w sensie metryki
 (taksówkowej).

 

Można udowodnić, że zbieżność w
 jest równoważna zbieżności po każdej
            współrzędnej osobno.

 

 

 

 

DEFINICJA 8.11     (PUNKT SKUPIENIA)

 

           



               

 

 

 

WNIOSEK:

 

             A jest zbiorem domkniętym wtedy i tylko wtedy jeżeli A zawiera wszystkie swoje punkty skupienia.

 

       

 

 

       

---