Zadana liczba iteracji - iter = 50
Zadana dokładność obliczeń - eps = 1.0000E-0006
Układ sprowadzono do postaci normalnej.
Macierz współczynników:
wiersz nr 1
2.0000000E+0000 1.0000000E+0000 -1.0000000E+0000
wiersz nr 2
1.0000000E+0000 3.0000000E+0000 -1.0000000E+0000
wiersz nr 3
1.0000000E+0000 -1.0000000E+0000 2.0000000E+0000
Wektor prawych stron:
1.0000000E+0000 4.0000000E+0000 5.0000000E+0000
Liczba wykonanych iteracji: 21
Rozwiązanie układu równań:
9.9999993E-0001 2.0000002E+0000 3.0000002E+0000
2.7. Ekstremalne wartości własne
Działanie macierzy kwadratowej ![]()
na wektor X
(2.131)
możemy traktować jako operację liniową przejawiającą się w zmianie długości i kierunku wektora X. Jeśli przekształcenie to transformuje wektor X na siebie samego (tak, żeby wektor był równoległy do wektora X )
![]()
(2.132)
to liczbę nazywamy wartością własną macierzy A , a wektor X - wektorem własnym. Działanie macierzy A na wektor własny X możemy więc zastąpić pomnożeniem tego wektora przez liczbę, co umożliwia jakościowe uproszczenie rozwiązywania wielu zagadnień matematycznych i fizycznych.
Wartości własne macierzy A są pierwiastkami wielomianu charakterystycznego (2.13) tej macierzy
(2.133)
W obliczeniach numerycznych rzadko jednak wyznaczamy pierwiastki tego wielomianu, gdyż często zadanie to jest źle uwarunkowane - podczas gdy dobrze jest uwarunkowane zadanie pierwotne, ze względu na macierz A.
Dlatego też na ogół macierz A przekształcamy bez rozwijania jej wyznacznika charakterystycznego - do bardziej dogodnych postaci, umożliwiających obliczanie wartości własnych na podstawie różnych twierdzeń algebry liniowej [1 - 3, 6, 9].
Przy rozwiązywaniu wielu zadań wystarczająca jest znajomość wartości własnych: maksymalnej i minimalnej co do modułu np. alternatywna definicja wskaźnika uwarunkowania macierzy A (2.43): [6, 7], a najczęściej tylko maksymalnej np. (2.14) lub (2.130). Ograniczymy się więc do przedstawienia kilku prostych algorytmów obliczania ekstremalnych co do modułu wartości własnych macierzy o elementach rzeczywistych, omawianych m.in. w pracach [2, 8].
Mnożąc lewostronnie zależność dla k-tej wartości własnej i k-tego wektora własnego
(2.134)
przez macierz A otrzymamy
i po m-krotnym powtórzeniu tej operacji mamy
(2.135)
Podobnie mnożąc lewostronnie (2.134) przez dostajemy
i w ogólnym przypadku słuszna jest zależność
(2.136)
Po wykorzystaniu zależności (2.135) i (2.136) z twierdzenia, że suma wartości własnych macierzy A jest równa jej śladowi
(2.137)
wynika wniosek, że
(2.138)
dla dowolnej, całkowitej liczby m.
W przypadku, gdy maksymalna co do modułu wartość własna jest pierwiastkiem rzeczywistym i pojedynczym równania charakterystycznego (2.133)
(2.139)
na mocy (2.138) uzyskujemy związek
(2.140)
z którego, gdy m rośnie nieograniczenie mamy
![]()
(2.141)
Również w przypadku, gdy maksymalna co do modułu wartość własna jest rzeczywistym pierwiastkiem q-krotnym równania charakterystycznego (2.133)
(2.142)
jej wartość wyraża się wzorem (2.140), gdyż we wzorze (2.140) zarówno w liczniku, jak i w mianowniku będzie występowała jednakowa liczba jedynek
Po obliczeniu ze wzoru (2.141) nie wiadomo zatem, czy jest to pierwiastek pojedynczy czy też pierwiastek wielokrotny. Krotność pierwiastka rzeczywistego
o maksymalnej co do modułu wartości własnej możemy jednak łatwo obliczyć z zależności (2.138)
(2.143)
dla dostatecznie dużych m.
Wprowadzając we wzorze (2.138) wykładnik całkowity ujemny możemy w ana-logiczny sposób wyznaczyć minimalną co do modułu wartość własną macierzy A.
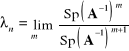
(2.144)
oraz jej krotność
(2.145)
odwracając uprzednio macierz A.
Maksymalną co do modułu wartość własną będącą pojedynczym pierwiastkiem zespolonym równania charakterystycznego (2.133)
(2.146)
można również obliczyć opierając się na własności (2.138).
Zapisując i w postaci wykładniczej
otrzymujemy
![]()
i następnie uzyskujemy zależność
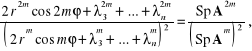
z której dla dostatecznie dużych m mamy
(2.147)
Podstawiając uzyskane wyrażenie (2.147) do zależności
![]()
ostatecznie otrzymujemy
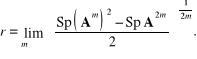
(2.148)
Do sprawdzenia prawidłowości wyznaczonych ekstremalnych wartości własnych i lokalizacji następnych pierwiastków równania charakterystycznego (2.133) można - oprócz (2.137) - wykorzystywać inne twierdzenia o wartościach własnych:
1. Jeżeli macierz A jest macierzą symetryczną o elementach rzeczywistych, to jej wartości własne i wektory własne są rzeczywiste.
2. Twierdzenie Perrona. Jeśli macierz A jest macierzą o elementach rzeczywistych dodatnich, to jej największa co do modułu wartość własna jest dodatnia i jest pojedynczym pierwiastkiem równania charakterystycznego, a odpowiadający jej wektor własny ma składowe dodatnie.
3. Twierdzenie Gerszgorina. Wszystkie wartości własne macierzy A leżą w obszarze, będącym sumą teoriomnogościową kół ![]()
o środkach oraz promieniach
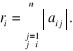
Twierdzenie Gerszgorina, dla macierzy 4 stopnia o elementach rzeczywistych ilustruje rysunek 2.3.
Znając wartość własną i odpowiadający jej wektor własny (obliczony np. przy przyjęciu dodatkowego warunku dotyczącego długości tego wektora) można również wyznaczyć drugą wartość własną i następne wartości własne metodą redukcji, korzystając z możliwości rozkładu dowolnego wektora względem różnych między sobą wektorów własnych [2, 13].
Rys. 2.3
Znajomość wektorów własnych jest szczególnie istotna dla macierzy A symetrycznych o elementach rzeczywistych, gdyż np. dla macierzy kwadratowej, której kolumny są wektorami własnymi
można udowodnić zależność [6, 7]
oraz wykazać ortogonalność (2.30) macierzy S.
Obliczanie ekstremalnych co do modułu wartości własnych za pomocą wzorów (2.141), (2.143) ÷ (2.145) oraz (2.148) odbywa się w programie 2.4; tabulogram modułu Obliczenia tego programu jest następujący:
{Program 2.4}
unit Obliczenia;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls,
Forms, Dialogs, StdCtrls, Buttons;
const nmax = 20;
type
Tabl1 = array [1..nmax,1..nmax] of Real;
Tabl2 = array [1..nmax,1..2*nmax] of Real;
. . . . . . . . . . . . . . . . . . . . . .
var
Form3: TForm3;
bl,det,lam,lam1,eps,r,r1,s,Spm,Spm1: Real;
i,j,k,n,m,q,war: Integer;
A,Am,Am1: Tabl1;
nazwa: String;
rep: Boolean;
plik: Text;
B: Tabl2;
implementation
uses Ustawienia, Informacje, Grafika, Podglad;
label kon,omin,powt;
{$R *.DFM}
{procedure ElimGaussa(n,m: Integer; var A: Tabl2; var det: Real);}
procedure TForm3.FormCreate(Sender: TObject);
begin
nazwa:='Dane1.dan';
Dane.Lines.Text:='';
end;
procedure TForm3.BitBtn1Click(Sender: TObject);
label omin,kon,powt;
begin
Form2.Show;
AssignFile(plik,nazwa);
Reset(plik);
Readln(plik,n,eps);
for i:=1 to n do
for j:=1 to n do
Read(plik,A[i,j]);
CloseFile(plik);
if RadioButton1.Checked then war:=1;
if RadioButton2.Checked then war:=2;
if RadioButton3.Checked then war:=3;
AssignFile(plik,Edit1.Text);
Rewrite(plik);
Writeln(plik,'PROGRAM 2.4.');
if war=1 then begin
Writeln(plik,'Obliczanie wartości własnej o module max');
Writeln(plik,'i jej krotności.');
end;
if war=2 then begin
Writeln(plik,'Obliczanie ekstremalnych wartości własnych');
Writeln(plik,'i ich krotności.');
end;
if war=3 then begin
Writeln(plik,'Obliczanie maksymalnego modułu zespolonej');
Writeln(plik,'wartości własnej.');
end;
Writeln(plik);
Writeln(plik,'Stopień macierzy - n = ',n:2);
Writeln(plik,'Dokładność obliczeń - eps = ',eps:11);
Writeln(plik);
Writeln(plik,'Macierz współczynników:');
for i:=1 to n do begin
Writeln(plik,' wiersz nr ',i:2);
k:=0; Write(plik,' ');
for j:=1 to n do begin
k:=k+1;
if k=5 then begin
k:=0; Writeln(plik);
Write(plik,' ');
end;
Write(plik,' ',A[i,j]:13);
end;
Writeln(plik);
end;
Writeln(plik);
rep:=False;
powt:
m:=2; Spm:=0;
for i:=1 to n do
Spm:=Spm+A[i,i];
for i:=1 to n do
for j:=1 to n do begin
s:=0;
for k:=1 to n do
s:=s+A[i,k]*A[k,j];
Am[i,j]:=s;
end;
Spm1:=0;
for i:=1 to n do
Spm1:=Spm1+Am[i,i];
if not rep then lam:=Spm1/Spm
else lam:=Spm/Spm1;
if war=3 then begin
r:=Exp(0.5/m*Ln(0.5*Abs(Spm*Spm-Spm1)));
goto omin;
end;
Spm:=Spm1;
repeat
for i:=1 to n do
for j:=1 to n do begin
s:=0;
for k:=1 to n do
s:=s+A[i,k]*Am[k,j];
Am1[i,j]:=s;
end;
Spm1:=0;
for i:=1 to n do
Spm1:=Spm1+Am1[i,i];
if not rep then lam1:=Spm1/Spm
else lam1:=Spm/Spm1;
bl:=Abs(lam1-lam);
for i:=1 to n do
for j:=1 to n do
Am[i,j]:=Am1[i,j];
Spm:=Spm1; lam:=lam1;
m:=m+1;
until bl<eps;
s:=1;
for i:=1 to m do
if not rep then s:=s*lam
else s:=s*(1/lam);
q:=Round(Spm/s);
if not rep then begin
Write(plik,'Wartość własna o module max: ');
Writeln(plik,lam:16);
Write(plik,'Krotność max wartości własnej - q: ');
Writeln(plik,q:2);
Write(plik,'Liczba potęgowań macierzy zadanej - m: ');
Writeln(plik,m:2);
Writeln(plik);
end else begin
Write(plik,'Wartość własna o module min: ');
Writeln(plik,lam:16);
Write(plik,'Krotność min wartości własnej - q: ');
Writeln(plik,q:2);
Write(plik,'Liczba potęgowań macierzy odwrotnej - m: ');
Writeln(plik,m:2);
Writeln(plik);
end;
if (war=1) or rep then goto kon;
for i:=1 to n do
for j:=1 to n do begin
B[i,j]:=A[i,j];
if i=j then B[i,n+j]:=1
else B[i,n+j]:=0;
end;
ElimGaussa(n,n,B,det);
Writeln(plik,'Macierz odwrotna:');
for i:=1 to n do begin
Writeln(plik,' wiersz nr ',i:2);
k:=0; Write(plik,' ');
for j:=1 to n do begin
k:=k+1;
if k=5 then begin
k:=0; Writeln(plik);
Write(plik,' ');
end;
Write(plik,' ',B[i,n+j]:13);
end;
Writeln(plik);
end;
Writeln(plik);
for i:=1 to n do
for j:=1 to n do
A[i,j]:=B[i,n+j];
if not rep then begin
rep:=True;
goto powt;
end;
omin:
m:=3;
repeat
for i:=1 to n do
for j:=1 to n do begin
s:=0;
for k:=1 to n do
s:=s+A[i,k]*Am[k,j];
B[i,j]:=s;
end;
Spm:=0;
for i:=1 to n do
Spm:=Spm+B[i,i];
for i:=1 to n do
for j:=1 to n do begin
s:=0;
for k:=1 to n do
s:=s+B[i,k]*B[k,j];
Am1[i,j]:=s;
end;
Spm1:=0;
for i:=1 to n do
Spm1:=Spm1+Am1[i,i];
r1:=Exp(0.5/m*Ln(0.5*Abs(Spm*Spm-Spm1)));
bl:=Abs(r1-r);
for i:=1 to n do
for j:=1 to n do
Am[i,j]:=B[i,j];
m:=m+1; r:=r1;
until bl<eps;
Write(plik,'Max moduł zespolonej wartości własnej: ');
Writeln(plik,r:16);
Write(plik,'Liczba potęgowań macierzy zadanej - m: ');
Writeln(plik,m:2);
Writeln(plik);
kon:
CloseFile(plik);
Form2.Wyniki.Lines.LoadFromFile(Edit1.Text);
end;
. . . . . . . . . . . . . . . . . . . . . .
end.
Rys. 2.4
Wczytywane przez program 2.4 dane z pliku o nazwie pr_2_4.dan zawierają: stopień macierzy n, dokładność obliczania granicy ciągów (2.141), (2.144) lub (2.148) oraz zapisane wierszami współczynniki macierzy A. Wybór alternatywy obliczeń jest dokonywany na formularzu Dane (rys. 2.4) poprzez zaznaczenie odpowiednigo pola obok zamieszczonego opisu jednego z trzech rozważanych przypadków wyznaczania ekstremalnych wartości własnych.
Za pomocą programu 2.4 obliczono ekstremalne wartości własne następujących macierzy:
Przykład 1
.
Wielomian charakterystyczny
![]()
Wartości własne:
PROGRAM 2.4.
Obliczanie ekstremalnych wartości własnych
i ich krotności.
Stopień macierzy - n = 3
Dokładność obliczeń - eps = 1.00E-0006
Macierz współczynników:
wiersz nr 1
2.0000E+0000 -2.0000E+0000 3.0000E+0000
wiersz nr 2
1.0000E+0000 1.0000E+0000 1.0000E+0000
wiersz nr 3
1.0000E+0000 3.0000E+0000 -1.0000E+0000
Wartość własna o module max: 3.0000003E+0000
Krotność max wartości własnej - q: 1
Liczba potęgowań macierzy zadanej - m: 42
Macierz odwrotna:
wiersz nr 1
6.6667E-0001 -1.1667E+0000 8.3333E-0001
wiersz nr 2
-3.3333E-0001 8.3333E-0001 -1.6667E-0001
wiersz nr 3
-3.3333E-0001 1.3333E+0000 -6.6667E-0001
Wartość własna o module min: 9.9999982E-0001
Krotność min wartości własnej - q: 1
Liczba potęgowań macierzy odwrotnej - m: 24
Przykład 2
.
Wielomian charakterystyczny
Wartości własne:
![]()
PROGRAM 2.4.
Obliczanie ekstremalnych wartości własnych
i ich krotności.
Stopień macierzy - n = 4
Dokładność obliczeń - eps = 1.00E-0010
Macierz współczynników:
wiersz nr 1
1.0000E+0000 2.0000E+0000 3.0000E+0000 4.0000E+0000
wiersz nr 2
2.0000E+0000 1.0000E+0000 2.0000E+0000 3.0000E+0000
wiersz nr 3
3.0000E+0000 2.0000E+0000 1.0000E+0000 2.0000E+0000
wiersz nr 4
4.0000E+0000 3.0000E+0000 2.0000E+0000 1.0000E+0000
Wartość własna o module max: 9.0990195E+0000
Krotność max wartości własnej - q: 1
Liczba potęgowań macierzy zadanej - m: 29
Macierz odwrotna:
wiersz nr 1
-4.0000E-0001 5.0000E-0001 0.0000E+0000 1.0000E-0001
wiersz nr 2
5.0000E-0001 -1.0000E+0000 5.0000E-0001 3.6380E-0013
wiersz nr 3
0.0000E+0000 5.0000E-0001 -1.0000E+0000 5.0000E-0001
wiersz nr 4
1.0000E-0001 -2.8422E-0014 5.0000E-0001 -4.0000E-0001
Wartość własna o module min: -5.8578644E-0001
Krotność min wartości własnej - q: 1
Liczba potęgowań macierzy odwrotnej - m: 36
Przykład 3
.
Wielomian charakterystyczny
![]()
Wartości własne:
![]()
![]()
PROGRAM 2.4.
Obliczanie ekstremalnych wartości własnych
i ich krotności.
Stopień macierzy - n = 4
Dokładność obliczeń - eps = 1.00E-0003
Macierz współczynników:
wiersz nr 1
1.0000E+0000 3.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 2
2.0000E+0000 5.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 3
0.0000E+0000 0.0000E+0000 2.0000E+0000 -3.0000E+0000
wiersz nr 4
0.0000E+0000 0.0000E+0000 -6.0000E+0000 2.0000E+0000
Wartość własna o module max: 6.2048977E+0000
Krotność max wartości własnej - q: 2
Liczba potęgowań macierzy zadanej - m: 11
Macierz odwrotna:
wiersz nr 1
-5.0000E+0000 3.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 2
2.0000E+0000 -1.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 3
0.0000E+0000 0.0000E+0000 -1.4286E-0001 -2.1429E-0001
wiersz nr 4
0.0000E+0000 0.0000E+0000 -4.2857E-0001 -1.4286E-0001
Wartość własna o module min: -1.6232873E-0001
Krotność min wartości własnej - q: 1
Liczba potęgowań macierzy odwrotnej - m: 4
W tym przykładzie wartości własne i są bliskie sobie, co spowodowało wyznaczenie jednej podwójnej wartości własnej o maksymalnym module - równej ![]()
O tym, że nie jest to wartość własna zadanej macierzy A możemy zorientować się z przebiegu obliczeń i bardzo wolnej zbieżności ciągu (2.141).
Przykład 4
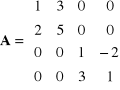
.
Wielomian charakterystyczny
![]()
Wartości własne:
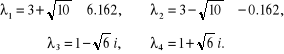
PROGRAM 2.4.
Obliczanie ekstremalnych wartości własnych
i ich krotności.
Stopień macierzy - n = 4
Dokładność obliczeń - eps = 1.00E-0006
Macierz współczynników:
wiersz nr 1
1.0000E+0000 3.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 2
2.0000E+0000 5.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 3
0.0000E+0000 0.0000E+0000 1.0000E+0000 -2.0000E+0000
wiersz nr 4
0.0000E+0000 0.0000E+0000 3.0000E+0000 1.0000E+0000
Wartość własna o module max: 6.1622789E+0000
Krotność max wartości własnej - q: 1
Liczba potęgowań macierzy zadanej - m: 20
Macierz odwrotna:
wiersz nr 1
-5.0000E+0000 3.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 2
2.0000E+0000 -1.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 3
0.0000E+0000 0.0000E+0000 1.4286E-0001 2.8571E-0001
wiersz nr 4
0.0000E+0000 0.0000E+0000 -4.2857E-0001 1.4286E-0001
Wartość własna o module min: -1.6227738E-0001
Krotność min wartości własnej - q: 1
Liczba potęgowań macierzy odwrotnej - m: 6
Przykład 5
Wielomian charakterystyczny
![]()
Wartości własne:
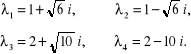
PROGRAM 2.4.
Obliczanie maksymalnego modułu zespolonej
wartości własnej.
Stopień macierzy - n = 4
Dokładność obliczeń - eps = 1.00E-0004
Macierz współczynników:
wiersz nr 1
1.0000E+0000 -2.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 2
3.0000E+0000 1.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 3
0.0000E+0000 0.0000E+0000 2.0000E+0000 -2.0000E+0000
wiersz nr 4
0.0000E+0000 0.0000E+0000 5.0000E+0000 2.0000E+0000
Max moduł zespolonej wartości własnej: 3.7411953E+0000
Liczba potęgowań macierzy zadanej - m: 20
Przykład 6
.
Wielomian charakterystyczny
![]()
Wartości własne:
![]()
PROGRAM 2.4.
Obliczanie maksymalnego modułu zespolonej
wartości własnej.
Stopień macierzy - n = 4
Dokładność obliczeń - eps = 1.00E-0004
Macierz współczynników:
wiersz nr 1
1.0000E+0000 0.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 2
0.0000E+0000 1.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 3
0.0000E+0000 0.0000E+0000 2.0000E+0000 -2.0000E+0000
wiersz nr 4
0.0000E+0000 0.0000E+0000 5.0000E+0000 2.0000E+0000
Max moduł zespolonej wartości własnej: 3.7416525E+0000
Liczba potęgowań macierzy zadanej - m: 9
Przykład 7
.
Wielomian charakterystyczny
![]()
Wartości własne:
![]()
PROGRAM 2.4.
Obliczanie ekstremalnych wartości własnych
i ich krotności.
Stopień macierzy - n = 4
Dokładność obliczeń - eps = 1.00E-0004
Macierz współczynników:
wiersz nr 1
5.0000E+0000 0.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 2
0.0000E+0000 5.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 3
0.0000E+0000 0.0000E+0000 1.0000E+0000 -3.0000E+0000
wiersz nr 4
0.0000E+0000 0.0000E+0000 2.0000E+0000 -5.0000E+0000
Wartość własna o module max: 4.9999638E+0000
Krotność max wartości własnej - q: 2
Liczba potęgowań macierzy zadanej - m: 41
Macierz odwrotna:
wiersz nr 1
2.0000E-0001 0.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 2
0.0000E+0000 2.0000E-0001 0.0000E+0000 0.0000E+0000
wiersz nr 3
0.0000E+0000 0.0000E+0000 -5.0000E+0000 3.0000E+0000
wiersz nr 4
0.0000E+0000 0.0000E+0000 -2.0000E+0000 1.0000E+0000
Wartość własna o module min: -2.6796046E-0001
Krotność min wartości własnej - q: 1
Liczba potęgowań macierzy odwrotnej - m: 5
Przykład 8
.
Wielomian charakterystyczny
![]()
Wartości własne:
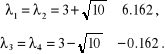
PROGRAM 2.4.
Obliczanie ekstremalnych wartości własnych
i ich krotności.
Stopień macierzy - n = 4
Dokładność obliczeń - eps = 1.00E-0006
Macierz współczynników:
wiersz nr 1
1.0000E+0000 3.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 2
2.0000E+0000 5.0000E+0000 0.0000E+0000 0.0000E+0000
wiersz nr 3
0.0000E+0000 0.0000E+0000 1.0000E+0000 3.0000E+0000
wiersz nr 4
0.0000E+0000 0.0000E+0000 2.0000E+0000 5.0000E+0000
112 2. Układy równań liniowych
2.7. Ekstremalne wartości własne 119
Wyszukiwarka