POLITECHNIKA ŚLĄSKA W GLIWICACH

WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA

Katedra Informatyki i Ekonometrii

Projekt z przedmiotu:

Ekonometria

Przyjazdy cudzoziemców do Polski

Wykonała:

Kierunek: ZIP 22

Miasto: Zabrze

Sekcja: 2

Spis treści:

Wstęp

Tematem niniejszej pracy jest zagadnienie przyjazdów cudzoziemców do Polski
w latach 1989-2004. Dzięki wzrostowi gospodarczemu obserwowanemu w kraju, Polska staje się coraz bardziej atrakcyjna dla obcokrajowców. Powstaje coraz więcej inwestycji zagranicznych. Można powiedzieć, że ma to pośredni wpływ na rozwój turystyki w naszym kraju.

Opisywany model ekonometryczny będzie „badał” zjawisko napływu obcokrajowców do Polski pod względem turystycznym. Jest to badana cecha ilościowa, a więc będzie to zmienna objaśniana, nazywana również zmienną endogeniczną. Na podstawie stworzonego modelu, będzie można ocenić jak bardzo atrakcyjna jest Polska dla turystów zagranicznych. Skoro model będzie badał „zjawisko turystyczne”, ustaliłam 4 zmienne objaśniające, nazywane zmiennymi egzogenicznymi, biorąc pod uwagę aspekty turystyczne. Są to:

• Liczba placówek gastronomicznych - restauracji;

• Szlaki turystyczne górskie;

• Liczba turystycznych obiektów zbiorowego zakwaterowania;

• Liczba pomników przyrody.

Dane statystyczne zaczerpnęłam z roczników statystycznych GUS 1990-2005. Przygotowana baza danych statystycznych, nazywana szeregiem czasowym, ma postać:

Lata	Y	X1	X2	X3	X4
1989	8,233	9,632	9,112	8,056	18,876
1990	19,583	8,453	9,246	8,188	18,876
1991	36,846	8,154	9,341	10,987	19,985
1992	49,015	8,035	9,360	11,863	20,896
1993	60,951	4,214	8,850	12,583	22,151
1994	74,253	4,486	8,950	6,431	23,529
1995	82,244	4,857	8,990	7,585	26,423
1996	87,439	5,180	8,700	7,364	30,205
1997	87,817	5,010	8,950	7,578	30,811
1998	88,592	6,237	10,579	7,918	33,231
1999	89,118	7,140	11,117	7,704	33,243
2000	84,515	8,519	10,573	7,818	33,094
2001	61,431	8,725	10,573	7,613	33,781
2002	50,735	8,813	11,155	7,050	33,882
2003	52,130	8,785	10,469	7,116	33,865
2004	61,918	9,195	11,119	6,972	34,385
Y - przyjazdy cudzoziemców do Polski w tys. osób
X1 - liczba placówek gastronomicznych - restauracji w mln. (stan w dn. 31 XII)
X2 - szlaki turystyczne górskie (w tys. km)
X3 - liczba turystycznych obiektów zbiorowego zakwaterowania w mln. sztuk (stan w dn. 31 XII)
X4 - liczba pomników przyrody w tys. (stan w dn. 31 XII)
Źródło: Roczniki statystyczne 1990 - 2005

Dla powyższej bazy danych statystycznych, badam zależności między zmienną objaśnianą a poszczególnymi zmiennymi objaśniającymi. Każdą zbadaną zależność przedstawiam na wykresie, na podstawie którego stwierdzam, że są to funkcje wielomianowe. Model natomiast ma być modelem liniowym (zależności liniowe). Wobec tego przekształcam dane na:

Lata	Y	X1	X2	X3	X4
1989	8,233	92,775	83,029	64,899	356,303
1990	19,583	71,453	85,489	67,043	356,303
1991	36,846	66,488	87,254	120,714	399,400
1992	49,015	64,561	87,610	140,731	436,643
1993	60,951	17,758	78,323	158,332	490,667
1994	74,253	20,124	80,103	41,358	553,614
1995	82,244	23,590	80,820	57,532	698,175
1996	87,439	26,832	75,690	54,228	912,342
1997	87,817	25,100	80,103	57,426	949,318
1998	88,592	38,900	111,915	62,695	1 104,299
1999	89,118	50,980	123,588	59,352	1 105,097
2000	84,515	72,573	111,788	61,121	1 095,213
2001	61,431	76,126	111,788	57,958	1 141,156
2002	50,735	77,669	124,434	49,703	1 147,990
2003	52,130	77,176	109,600	50,637	1 146,838
2004	61,918	84,548	123,632	48,609	1 182,328

1. Ustalenie postaci modelu

Ustalenie postaci polega na ustaleniu zależności funkcyjnej modelu. W tym przypadku będzie miała ona postać:

i = 1,2,...,16

Składnik losowy
uwzględnia:

• wpływ czynników (zmiennych) nieuwzględnionych przy ustalaniu zmiennych objaśniających dla budowanego modelu;

• błędy pomiaru wartości w bazie danych statystycznych;

• wpływ czynników losowych na zmienną endogeniczną;

• różnice pomiędzy rzeczywistą zależnością zmiennej objaśnianej od zmiennych objaśniających a przyjętą postacią modelu.

Budowany model będzie miał więc postać:

gdzie:

- zmienna objaśniana,

,
,
,
- zmienne objaśniające,

,
,
,
,
- parametry strukturalne modelu,

- składnik losowy.

2. Dobór zmiennych do modelu

W modelu powinny znaleźć się zmienne, które wykazują odpowiednio wysoką zmienność. Inaczej mówiąc, z modelu eliminuję zmienne quasi-stałe. Zmienne, które pozostaną w modelu powinny wykazywać:

• Odpowiednio silne liniowe powiązanie ze zmienną objaśnianą;

• Odpowiednio słabe liniowe powiązanie z innymi zmiennymi objaśniającymi.

Siłę powiązania liniowego zmiennych bada się za pomocą współczynnika korelacji.
Już na podstawie obliczonych współczynników korelacji między zmienną objaśnianą
a poszczególnymi zmiennymi objaśniającymi, można stwierdzić, że zmienne
,
nie mają istotnego wpływu na zmienną objaśnianą. W dodatku zmienna
wykazuje silną zależność ze zmiennymi
,
.

2.1. Metoda grafów

Aby mieć pewność, że zmienne będą dobrze dobrane, dobieram je za pomocą metody grafów bądź metody wskaźników pojemności informacyjnej (metody Hellwiga). Dobór metodą grafów przedstawię w postaci grafu końcowego, gdyż w dalszych etapach budowy modelu będę korzystać z metody Hellwiga. Dla obu metod buduję wektor współczynników korelacji między zmiennymi objaśniającymi a zmienną objaśnianą oraz macierz współczynników korelacji miedzy kolejnymi zmiennymi objaśniającymi, wg schematu:

• Wektor współczynników korelacji między zmiennymi objaśniającymi
  a zmienną objaśnianą:

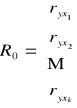
• Macierz współczynników korelacji między kolejnymi zmiennymi objaśniającymi:

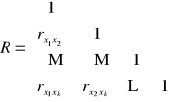
Mają one postać:

Wektor współczynników korelacji między zmiennymi objaśniającymi a zmienną objaśnianą				Macierz współczynników korelacji miedzy kolejnymi zmiennymi objaśniającymi
	-0,64024			1	0,540367	-0,13555	0,127995
R0 =	0,159938		R =	0,540367	1	-0,36532	0,773473
	-0,26265			-0,13555	-0,36532	1	-0,57162
	0,594592			0,127995	0,773473	-0,57162	1

Dobierając zmienne metodą grafów, otrzymuję graf:

Do modelu wejdzie zmienna X4, bo ma najwięcej powiązań z innymi zmiennymi i jest silniej skorelowana ze zmienną objaśnianą od zmiennej X2. Wobec tego model będzie miał postać:

Postać ta wskazuje na to, że przyjazdy obcokrajowców do Polski najlepiej objaśnia liczba pomników przyrody.

2.2. Metoda wskaźników pojemności informacyjnej

Dobór zmiennych przeprowadzam również za pomocą metody Hellwiga, gdyż to na jej podstawie przeprowadzę kolejne kroki budowy modelu ekonometrycznego.

Tworzę wszystkie kombinacje jednoelementowe, dwuelementowe, aż do
k-elementowych ze zmiennych objaśniających. Liczbę kombinacji obliczam ze wzoru:

gdzie: k - liczba zmiennych objaśniających z bazy danych statystycznych.

W tym przypadku liczba kombinacji wynosi 15 (od C1 do C15). Dla każdej kombinacji C
i każdej zmiennej objaśniającej wchodzącej w skład tej kombinacji, obliczam indywidualny wskaźnik pojemności informacyjnej ze wzoru:

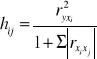
przy czym:
.

Następnie dla każdej kombinacji C, obliczam integralny wskaźnik pojemności informacyjnej ze wzoru:

przy czym:
.

Dla modelu wybieram zmienne z kombinacji, dla której integralny wskaźnik pojemności informacyjnej jest najwyższy. Wnosi on najwięcej informacji i jest nazywany wskaźnikiem pojemności optymalnej.

W przypadku budowanego modelu będzie to wskaźnik:

H7 =

0,723334

Wskaźnik ten jest wskaźnikiem kombinacji C₇={X1,X4}. Do modelu wejdą więc zmienne: X1 i X4, a model będzie miał postać:

.

Zmienne X1 i X4 najlepiej objaśniają zmienną Y. A więc zjawisko przyjazdów cudzoziemców do Polski najlepiej „tłumaczą”: liczba placówek gastronomicznych (restauracji) oraz liczba pomników przyrody. Są też najsilniej z nią skorelowane.

3. Estymacja (szacowanie) parametrów strukturalnych modelu

Postać analityczna modelu ma charakter liniowy, a więc parametry strukturalne modelu podlegają szacowaniu Metodą Najmniejszych Kwadratów.

Zastosowanie MNK wymaga przyjęcia następujących założeń:

• Model, którego parametry są szacowane jest modelem liniowym;

• Wartości zmiennych objaśniających z bazy danych statystycznych są ustalone
  i znane (można zbudować macierz X);

• Wyznacznik X^TX jest różny od 0 (wśród zmiennych objaśniających nie zachodzi zjawisko współliniowości);

• Jedynymi danymi, z których korzysta się przy szacowaniu parametrów strukturalnych są dane z bazy danych statystycznych.

W pierwszej kolejności buduję wektor obserwacji zmiennej objaśnianej Y oraz macierz obserwacji zmiennych objaśniających X, wg schematu (dla tego modelu):

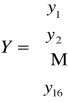
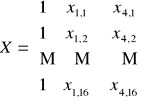
Ocenę a wektora parametrów strukturalnych
znajduje się przez zminimalizowanie funkcji:

Po zróżniczkowaniu względem wektora a i po rozwiązaniu równania okazuje się, że funkcja ta osiąga minimum w punkcie:

.

Wektor a będzie wektorem ocen parametrów strukturalnych modelu. Wobec tego, by oszacować parametry, wykonuję poszczególne obliczenia.

Po obliczeniu iloczynu macierzy X^TX, liczę wyznacznik powstałej macierzy. Jeśli wyznacznik jest różny od 0, to dana macierz jest nieosobliwa i posiada macierz odwrotną. Wyznacznik macierzy X^TX wynosi:

det(X^TX) =

263980716879,07

Wykonując dalsze obliczenia oraz podstawiając je do wzoru, otrzymuję wektor ocen parametrów strukturalnych:

	58,778
a =	-0,708
	0,052

Mając ten wektor zapisuję model w postaci:

Oszacowany model ma więc postać:

.

a jego interpretacja jest następująca:

• Jeżeli liczba placówek gastronomicznych wzrośnie o 1 mln. to zmaleje liczba przyjazdów cudzoziemców do Polski o 0,708 tys. osób, pod warunkiem, że nie zmieni się liczba pomników;

• Jeżeli liczba pomników przyrody wzrośnie o 1 tys. to wzrośnie liczba przyjazdów cudzoziemców do Polski o 0,052 tys. osób, pod warunkiem, że nie zmieni się liczba placówek gastronomicznych.

Kolejnym krokiem budowy modelu ekonometrycznego jest estymacja parametrów struktury stochastycznej. W tym celu wyznaczam reszty modelu, które są różnicą między empirycznymi a teoretycznymi wartościami zmiennej objaśnianej. Wartości teoretyczne zmiennej objaśnianej obliczam wg wzoru:

Suma wartości empirycznych zmiennej objaśnianej powinna równać się sumie wartości teoretycznych zmiennej objaśnianej, a więc suma reszt powinna być równa 0.

By wyznaczyć estymator wariancji składnika losowego (ocenę wariancji składnika losowego), korzystam ze wzoru:

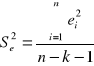
gdzie: k - liczba zmiennych objaśniających wchodzących do równania modelu.

Estymator wariancji składnika losowego wynosi więc:

=91,55258526.

Pierwiastkując ocenę składnika losowego otrzymuję odchylenie standardowe reszt, które informuje o średniej różnicy między wartościami rzeczywistymi a teoretycznymi zmiennej objaśnianej. Wynosi ono:

S_e=9,568311516

W następnej kolejności wyznaczam estymator macierzy wariancji i kowariancji ocen parametrów strukturalnych dla budowanego modelu ekonometrycznego - korzystam ze wzoru:

w macierzy tej na głównej przekątnej są wariancje ocen parametrów. Pierwiastkując te wartości, otrzymuję standardowe błędy szacunku parametru. Błąd taki informuje, o ile jedna wartość oceny parametru różni się od rzeczywistej wartości parametru. Błędy ocen parametrów strukturalnych modelu wynoszą:

D(a₀)=7,945 D(a₁)=0,096 D(a₂)=0,007.

Mając standardowe błędy ocen parametrów strukturalnych zapisuję ostateczną postać modelu (przy spełnionych założeniach MNK):

.

4. Weryfikacja modelu

4.1. Badanie dopuszczalności zbudowanego modelu

Badanie dopuszczalnego zbudowanego modelu polega na sprawdzeniu czy zbudowany model jest zgodny z teoriami ekonomicznymi, bada się tu zgodność zbudowanego modelu z bazą danych statystycznych.

By zbadać dopuszczalność modelu obliczam:

• Odchylenie standardowe reszt;

• Współczynnik zmienności resztowej;

• Współczynnik determinacji;

• Współczynnik zbieżności.

Odchylenie standardowe, obliczone wcześniej, wskazuje, że wartości teoretyczne zmiennej endogenicznej wyliczone z modelu teoretycznego różnią się średnio o 9,568 tys. od wartości rzeczywistych tej zmiennej.

Współczynnik zmienności resztowej liczy się w przypadku, gdy wartości rzeczywiste zmiennej objaśnianej w bazie danych są tego samego znaku. Dotyczy to również zbudowanego modelu.

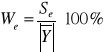
W zbudowanym modelu wskaźnik ten wynosi:

W_e=15,39%

oznacza to, że model w 15,39% jest wyjaśniany przez wartości przypadkowe. Inaczej mówiąc: informuje on, że 15,39% wartości
stanowi odchylenie standardowe reszt.

Kolejnym krokiem jest obliczenie współczynnika determinacji. Korzystam ze wzoru:

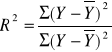
W zbudowanym modelu współczynnik ten wynosi:

R²=0,875240459

oznacza to, że 87,524% zmienności zmiennej objaśnianej zostało wyjaśnione przez dobrane zmienne objaśniające. W odniesieniu do badanego zjawiska: 87,524% zmienności przyjazdów cudzoziemców zostało wyjaśnione przez liczbę restauracji i liczbę pomników przyrody.

Na koniec tego badania, obliczam współczynnik zbieżności, korzystam przy tym ze wzoru:

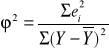
Współczynnik zbieżności wynosi więc:

=0,124759541

oznacza to, że 12,476% zmienności zmiennej objaśnianej nie zostało wyjaśnione przez dobrane zmienne objaśniające. Odnosząc to do badanego zjawiska: 12,476% zmienności przyjazdów obcokrajowców nie zostało wyjaśnione przez liczbę restauracji i liczbę pomników przyrody.

W ostatnim etapie tego badania, liczę współczynnik korelacji wielorakiej pomiędzy zmienną objaśnianą a zespołem dobranych do modelu zmiennych objaśniających. Wykorzystuję do tego policzony współczynnik determinacji, który jest współczynnikiem korelacji wielorakiej podniesionym do kwadratu. A więc, współczynnik korelacji wielorakiej wynosi:

R = 0,935542869

Wielkość współczynnika wskazuje na silną zależność między przyjazdami cudzoziemców do Polski a liczbą restauracji oraz liczbą pomników przyrody.

4.2. Badanie istotności współczynnika korelacji wielorakiej

Badanie to jest „badaniem dodatkowym”. Zgodnie z teoriami ekonometrycznymi, powinno przeprowadzać się go po przeprowadzeniu „obowiązkowych” badań. Są nimi:

• Badanie losowości składnika losowego;

• Badanie normalności rozkładu składnika losowego;

• Badanie stałości wariancji składnika losowego

• Badanie braku autokorelacji składnika losowego.

Kolejnym dodatkowym testem jest badanie istotności parametrów strukturalnych.
W praktyce jednak przyjęło się, te dwa badania przeprowadzać w pierwszej fazie weryfikacji statystycznych własności modelu liniowego, którego parametry zostały oszacowane MNK. Pozostałe badania sprawdzają czy dla zbudowanego modelu spełnione są założenia Klasycznej Metody Najmniejszych Kwadratów:

składnik losowy jest zmienną losową o wartości oczekiwanej równej 0 i stałej skończonej wariancji;

składnik losowy nie wykazuje autokorelacji.

Test istotności współczynnika korelacji wielorakiej pozwala stwierdzić czy model
w dostatecznym stopniu wyjaśnia badaną rzeczywistość. By przeprowadzić ten test należy przyjąć hipotezy:

Hipotezę bazową H0: R² = 0, która zakłada, że współczynnik korelacji wielorakiej nieistotnie różni się od 0;

Hipotezę alternatywną H1: R² ≠ 0, która zakłada, że współczynnik korelacji wielorakiej jest istotnie różny od 0.

Statystykę testu obliczam ze wzoru:

,

gdzie:

n - liczba obserwacji

k - liczba zmiennych objaśniających.

Dla danego modelu statystyka ta wynosi:

F =

45,60022

Kolejnym krokiem w przeprowadzanym teście jest odczytanie z tablic Fishera wartości krytycznej przy poziomie istotności α=0,05 i n₁=k oraz n₂=n-k-1. Odczytuję więc wartość krytyczną dla n₁=2 i n₂=13. wynosi ona:

F* =

3,81

F > F*

Wobec tego statystyka testu jest większa od wartości krytycznej odczytanej z tablic. Oznacza to, że należy odrzucić hipotezę bazową - współczynnik korelacji wielorakiej jest istotnie różny od 0. Model w odpowiednim stopniu wyjaśnia badaną rzeczywistość, czyli zbudowany model ekonometryczny w odpowiednim stopniu objaśnia zjawisko przyjazdów cudzoziemców do Polski.

4.3. Badanie istotności parametrów strukturalnych

W teście tym, jak w poprzednim, przyjmuję dwie hipotezy:

Hipotezę bazową H0: α_i = 0, która zakłada, że parametry strukturalne są nieistotnie różne od 0. Oznacza to, że dana zmienna objaśniająca nie wpływa w istotny sposób na zmienną objaśnianą;

Hipotezę alternatywną H1: α₁ ≠ 0, która zakłada, że parametry strukturalne istotnie różnią się od 0. Oznacza to, że dana zmienna objaśniająca ma istotny wpływ na zmienną objaśnianą.

Statystykę testu obliczam zgodnie z wzorem:

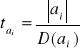
Statystykę obliczam dla każdej oceny parametru występującej w równaniu modelu. Tak więc:

t(a0) =	7,398
t(a1) =	7,373
t(a2) =	6,963

Wartość krytyczną odczytuję tablic rozkładu t-studenta dla poziomu istotności α=0,05 i n-k-1 stopni swobody. Wartość ta wynosi:

t* = 2,16.

W weryfikowanym modelu każda statystyka jest większa od wartości krytycznej odczytanej z tablic.

t(a0)>t*

t(a1)>t*

t(a2)>t*

Oznacza to odrzucenie hipotezy bazowej na rzecz hipotezy alternatywnej. A więc obie dobrane zmienne objaśniające mają istotny wpływ na zmienną endogeniczną. Zarówno liczba placówek gastronomicznych, jak i liczba pomników przyrody istotnie wpływają na napływ obcokrajowców do Polski w celach turystycznych.

4.4. Badanie losowości składnika losowego

Podobnie jak w poprzednich badaniach, przyjmuję dwie hipotezy:

Hipotezę bazową H0: rozkład reszt jest losowy;

Hipotezę alternatywną H1: rozkład reszt nie jest losowy.

Badanie to przeprowadza się za pomocą testu liczby serii, który pokazuje czy postać modelu została trafnie dobrana. Każdej reszcie przyporządkowuje się wartości logiczne a i b w zależności od znaku. Dla reszt dodatnich przyjmuje się wartość a, natomiast dla reszt ujemnych wartość b. W weryfikowanym modelu będzie to miało postać:

ei
-3,473	b
-7,211	b
4,291	a
13,155	a
-10,845	b
0,849	a
3,755	a
0,077	a
-2,698	b
-0,239	b
8,793	a
19,985	a
-2,980	b
-12,941	b
-11,835	b
1,319	a

Ciąg jednakowych wartości logicznych nazywa się serią. W tym modelu liczba serii wynosi:

k = 8.

By odczytać wartości krytyczne z tablic rozkładu liczby serii przyjmuję wartości:

n₁ - liczba reszt dodatnich n₂ - liczba reszt ujemnych.

Wynoszą one odpowiednio:

n₁ = 8 i n₂ = 8

Z tablic odczytuję wartość dolną k₁ dla α = 0,05 oraz n₁ i n₂, a także wartość górną
(z rozkładu prawostronnego) k₂ dla α = 0,95 oraz n₁ i n₂. wartości te wynoszą:

k₁ = 5 oraz k₂ = 12.

Liczba serii modelu mieści się w przedziale utworzonym przez wartości dolną i górną odczytane z tablic:

k₁ < k < k₂.

Oznacza to, że nie ma podstaw do odrzucenia hipotezy bazowej. Rozkład reszt jest losowy, a postać modelu została dobrze dobrana.

4.5. Badanie symetrii rozkładu reszt

W zbudowanym modelu liczba reszt dodatnich jest równa liczbie reszt ujemnych,
a więc nie wymagane jest przeprowadzenie testu symetrii. Rozkład reszt jest symetryczny.

4.6. Badanie normalności rozkładu składnika losowego

Badanie normalności rozkładu składnika losowego przeprowadzam za pomocą testu Hellwiga, który bada czy rozkład składnika losowego jest zgodny z rozkładem normalnym.

Jak w poprzednich testach, przyjmuję dwie hipotezy:

Hipotezę bazową H0: F(ζ_i) = F_N(ζ_i), która zakłada, że rozkład składnika losowego jest zgodny z rozkładem normalnym;

Hipotezę alternatywną H1: F(ζ_i) ≠ F_N(ζ_i), która zakłada, że rozkład składnika losowego nie jest zgodny z rozkładem normalnym.

By przeprowadzić ten test, należy dokonać standaryzacji reszt. Dlatego najpierw liczę odchylenie standardowe dla podanej próby. Należy pamiętać, że test ten przeprowadza się dla małej próby (<30). Odchylenie to wynosi:

Se =	8,907613255

Natomiast standaryzacji dokonuję zgodnie ze wzorem:

Kolejnym krokiem jest obliczenie wartości rozkładu normalnego dla zestandaryzowanej zmiennej u_i. Następnie tworzę cele, gdzie długość jednej celi wynosi
,
a więc 0,0625. Po ich stworzeniu, przypisuję kolejne wartości rozkładu normalnego zestandaryzowanej zmiennej do celi, w której przedziale się mieści ta wartość.

Przedstawia to tabela:

			Cele
ei	ui	(ui)	Początek celi	Koniec celi
-3,473	-0,390	0,348	0	0,0625
-7,211	-0,810	0,209	0,0625	0,125	***
4,291	0,482	0,685	0,125	0,1875
13,155	1,477	0,930	0,1875	0,25	*
-10,845	-1,218	0,112	0,25	0,3125
0,849	0,095	0,538	0,3125	0,375	**
3,755	0,422	0,663	0,375	0,4375	*
0,077	0,009	0,503	0,4375	0,5	*
-2,698	-0,303	0,381	0,5	0,5625	***
-0,239	-0,027	0,489	0,5625	0,625
8,793	0,987	0,838	0,625	0,6875	**
19,985	2,244	0,988	0,6875	0,75
-2,980	-0,335	0,369	0,75	0,8125
-12,941	-1,453	0,073	0,8125	0,875	*
-11,835	-1,329	0,092	0,875	0,9375	*
1,319	0,148	0,559	0,9375	1	*

* - liczba wartości rozkładu normalnego zestandaryzowanej zmiennej przyporządkowane do danej celi.

W następnym etapie testu zliczam puste cele. Liczba ta to : k = 6. Z tablic rozkładu Hellwiga odczytuję wartości k₁ i k₂ dla poziomu istotności α = 0,05 i n = 16 (liczba obserwacji). Wynoszą one:

k₁ = 3 oraz k₂ = 8.

Liczba pustych cel mieści się w przedziale utworzonym przez wartość odczytane z tablic.

k₁ < k < k₂.

Oznacza to, że nie ma podstaw do odrzucenia hipotezy bazowej, a co za tym idzie - rozkład reszt jest zgodny z rozkładem normalnym.

Dodatkowym testem sprawdzającym zgodność rozkładu reszt z rozkładem normalnym jest test Jarque Bera. Tak, jak w powyższym teście zakładam:

Hipotezę bazową H0: F(ζ_i) = F_N(ζ_i), która zakłada, że rozkład składnika losowego jest zgodny z rozkładem normalnym;

Hipotezę alternatywną H1: F(ζ_i) ≠ F_N(ζ_i), która zakłada, że rozkład składnika losowego nie jest zgodny z rozkładem normalnym.

By obliczyć statystykę dla tego testu korzystam ze wzoru:

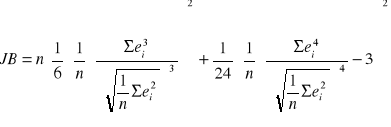
Następnie odczytuję wartość X² z tablic rozkładu Jarque Bera dla poziomu istotności
α = 0,05 i 2 stopni swobody. Wynosi ona 5,991. Natomiast obliczona statystyka jest równa:

JB =

0,77053

Wynika z tego, że statystyka JB jest mniejsza od wartości odczytanej z tablic, a co za tym idzie - nie ma podstaw do odrzucenia hipotezy bazowej, składnik losowy ma rozkład normalny.

4.7. Badanie braku autokorelacji składnika losowego.

W pierwszej kolejności przeprowadzam test autokorelacji Durbina-Wotsona, który zakłada, że jeżeli nie istnieje autokorelacja rzędu pierwszego, to nie istnieje inne autokorelacje składnika losowego.

W teście tym przyjmuję:

Hipotezę bazową: H0: δ₁ = 0, która zakłada, że autokorelacja jest nieistotnie różna od 0; brak autokorelacji rzędu pierwszego.

Następnym krokiem jest obliczenie statystyki testu. Korzystam ze wzoru:

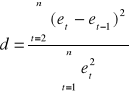
dla weryfikowanego modelu statystyka ta wynosi:

d =

1,6644873

Statystyka testu jest mniejsza od 2 (d < 2), a więc zakładam:

Hipotezę alternatywną H1: δ₁ > 0, która zakłada, że istnieje dodatnia autokorelacja rzędu pierwszego.

W następnej kolejności odczytuję z tablic wartości krytycznych statystycznych Durbina-Wotsona wartości d_u i d_l dla liczby obserwacji n i liczby zmiennych egzogenicznych modelu k. Wynoszą one:

dl =	0,74
du =	1,25

Wartość statystyki jest wyższa od wartości d_u odczytanej z tablic

d > d_u.

Wobec tego, nie ma podstaw do odrzucenia hipotezy bazowej, a więc autokorelacja jest nieistotnie różna od 0 - nie zachodzi zjawisko autokorelacji rzędu pierwszego.

Innym testem badającym zjawisko autokorelacji jest test oparty o statystykę
t-studenta, stosowany zamiennie za test Durbina-Wotsona. Służy on do badania autokorelacji rzędu dowolnego.

Zakłada się:

Hipotezę bazową H0: r_et,et-τ = 0, która zakłada, że autokorelacja rzędu τ jest nieistotnie różna od 0 (nie istnieje autokorelacja rzędu τ);

Hipotezę alternatywną H1: r_et,et-τ ≠ 0, która zakłada, że autokorelacja rzędu τ jest istotnie różna od 0 (istnieje autokorelacja rzędu τ).

Statystykę testu obliczam wg wzoru:

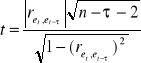
Statystykę tą liczę za każdym razem, gdy badam zjawisko autokorelacji rzędu τ. Następnie
z tablic rozkładu t-studenta odczytuję wartość krytyczną t* dla poziomu istotności α = 0,05
i n- τ-2 stopni swobody.

Jeżeli obliczona statystyka t ≤ t* to nie ma podstaw do odrzucenia hipotezy bazowej. Autokorelacja jest nieistotnie różna od 0, a więc nie zachodzi zjawisko autokorelacji rzędu τ.

Dla weryfikowanego modelu, przeprowadziłam badanie autokorelacji do rzędu 7. Wynikiem tego badania jest brak autokorelacji do rzędu 7.

Po wykonaniu tych testów, można stwierdzić, że model spełnia założenie KMNK mówiące o tym, że składnik losowy ma nie wykazywać autokorelacji.

4.8. Badanie stałości wariancji składnika losowego

Do badania stałości wariancji składnika losowego można posłużyć się jednym
z dwóch testów. W pierwszym z nich, zakłada się hipotezy:

Hipotezę bazową Ho: r_|et|,t = 0, która przyjmuje założenie, że nie zachodzi korelacja składnika losowego z czynnikiem czasu - wariancja jest stała w czasie;

Hipotezę alternatywną H1: r_”et|,t ≠ 0, która przyjmuje założenie, że korelacja składnika losowego z czynnikiem czasu jest istotnie różna od 0 - wariancja nie jest stała w czasie.

Do przeprowadzenia tego testu korzystam ze statystyki określonej wzorem :

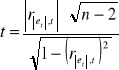
Wartość krytyczną t* odczytuję z tablic rozkładu t-studenta dla poziomu istotności α = 0,05 oraz n-2 stopni swobody. Statystyka testu oraz wartość krytyczna wynoszą:

t = 0,578971 oraz t* = 2,145.

Wartość statystyki jest mniejsza od wartości krytycznej odczytanej z tablic, a więc nie ma podstaw do odrzucenia hipotezy bazowej - korelacja składnika losowego z czynnikiem czasu jest nieistotnie różna od 0. Wariancja jest stała w czasie.

Stałość wariancji w czasie można zbadać jeszcze testem, w którym zakłada się hipotezy:

Hipotezą bazową H0:
, która zakłada, że wariancja pierwszej grupy reszt jest równa wariancji drugiej grupy reszt - zachodzi stałość wariancji
w czasie.

Hipotezę alternatywną H1:
, która zakłada, że wariancja pierwszej grupy reszt jest mniejsza od wariancji drugiej grupy reszt - nie zachodzi zjawisko stałości wariancji w czasie.

Statystyką tego testu jest:

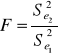
przy czym:
, gdzie i oznacza „numer grupy reszt”.

Przyjmuję następujący podział reszt:

ei
-3,473
-7,211
4,291
13,155
-10,845
0,849
3,755
0,077
-2,698
-0,239
8,793
19,985
-2,980
-12,941
-11,835
1,319

Z tablic Fishera odczytuję wartość krytyczną F* dla m₁=n₂-k-1 oraz m₂=n₁-k-1.

Dla weryfikowanego modelu statystyka testu oraz odczytana wartość krytyczna wynosi:

F = 2,067831 oraz F* = 5,05.

Wartość statystyki jest mniejsza od odczytanej wartości krytycznej, a więc nie ma podstaw do odrzucenia H0. Zachodzi stałość wariancji w czasie.

Po przeprowadzeniu tego badania, można stwierdzić, że model spełnia wszystkie założenia Klasycznej Metody Najmniejszych Kwadratów.

6. Wnioski

Ogólne miary dopasowania świadczą o tym, że oszacowany model ekonometryczny dobrze opisuje zmienność przyjazdów cudzoziemców do Polski w celach turystycznych
w zależności od liczby placówek gastronomicznych (w tym wypadku restauracji) oraz od liczby pomników przyrody. 87,524% zmienności zmiennej endogenicznej zostało objaśnianej przez oszacowany model. Wartości teoretyczne różnią się średnio o 9,568 tyś. od wartości rzeczywistych określających napływ obcokrajowców do Polski. Jest to stosunkowo niski odsetek całkowitej liczby przyjazdów zagranicznych turystów. Zmienne objaśniające istotnie wpływają na zmienną objaśnianą zarówno łącznie jak i oddzielnie. Świadczy o tym wysokość współczynnika korelacji wielorakiej oraz przeprowadzone badanie istotności parametrów strukturalnych. Parametry te wskazują na dobre dopasowanie modelu do danych empirycznych. Dzięki przeprowadzonemu badaniu normalności rozkładu składnika losowego, można stwierdzić, że postać liniowa została dobrze dopasowana do opisania analizowanego zjawiska. Rozkład normalny składnika losowego świadczy o tym, że składnik losowy nie powoduje w modelu poważniejszych zakłóceń. Model „przeszedł” wszystkie przeprowadzone testy z wynikiem pozytywnym, co może świadczyć tylko na jego korzyść.

Można stwierdzić, że stworzony model ekonometryczny bardzo dobrze odzwierciedla badaną rzeczywistość.

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

- 23 -

X1

X2

X4

X3

---