Nina Zarucka
Technologia chemiczna
Wydział Chemiczny
Ćwiczenie nr 27
Oznaczanie stałej szybkości i energi aktywacji jodowania acetonu
Ćwiczenie wykonano: 31.03.2003 r.
Sprawozdanie oddano:07.04.2003 r.
Część teoretyczna
Jodowanie acetonu jest reakcją autokatalizowaną przez jony wodorowe będące jednym z jej produktów.
CH3-CO-CH3 + J2 → CH3-CO-CH2 + H+ + J-
Jest to reakcja dwustopniowa, następcza
Etap I
Etap I jest powolny, odwracalny i decydujący o szybkości reakcji. Przebieg jest następujący:
Etap II CH3-C(OH)=CH2 + J2 → CH3-CO-CH2J + H+ + J-
W rezultacie szybkość całej reakcji zależy od stężenia acetonu (a-x) i kwasu (b+x), a nie zależy od stężeń jodu. Szybkość zamiany możemy wyrazić następującym wzorem:
![]()
lub po scałkowaniu ![]()
gdzie:
k - stała szybkości
a - początkowe stężenie acetonu
b - początkowe stężenie jonów wodorowych
x - ubytek stężenia acetonu(równy przyrostowi stężenia kwasu) po czasie t.
Energią aktywacji nazywamy minimum energii, jaką powinny być obdarzone cząsteczki, aby mogły przereagować. Można ją obliczyć na podstawie równania Arrheniusa:
![]()
Energię aktywacji można również obliczyć znając dwie stałe szybkości danej reakcji w dwóch różnych temperaturach ze wzoru:
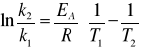
(*)
lub badając nachylenie prostej w układzie współrzędnych lnk = f(1/T).
2.Opis wykonywanych czynności
Doświadczenie wykonywałam dla dwóch temperatura T1=250C i T2=400C
Do kolb miarowych o pojemności 250 ml odmierzyłam 20 ml 1M kwasu solnego i 25 ml jodu. Mieszaniny rozcieńczyłam wodą destylowaną wstawiłam kolby do termostatów
Po ustaleniu się temperatur dodałam do kolb 2 ml acetonu, dopełniłam wodą do kreski i wymieszałam
Następnie pobrałam próbkę 25 ml i wlałam do kolby z przygotowanym wcześniej roztworem NaHCO3. Dodałam skrobi i miareczkowałam 0,02M Na2S2O3 do zaniku zabarwienia
Kolejnych pomiarów dokonywałam w odstępach 15 min (przy temperaturze 250C) i 10 min dla 400C
Wyniki zestawiam w tabeli
T1=250C
t[min] |
0 |
15 |
30 |
45 |
60 |
75 |
90 |
105 |
120 |
135 |
V[ml] |
12,1 |
11,7 |
11,2 |
10,6 |
10,0 |
9,7 |
9,1 |
8,5 |
8,1 |
7,6 |
T2=400C
t[min] |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
V[ml] |
11,8 |
9,80 |
7,70 |
5,60 |
3,50 |
1,60 |
0,10 |
0,05 |
Obliczenia
Stężenie początkowe acetonu a i kwasu b obliczam ze wzorów
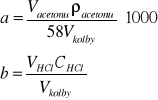
![]()
=0,79 g/cm3
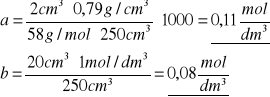
Ubytek stężenia acetonu obliczam ze wzoru
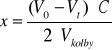
gdzie: Vo i Vt - ilości Na2S2O3 zużyte na miareczkowanie 25 dm3 mieszany reagującej na początku i po czasie t, c - stężenie Na2S2O3 [mol/dm3]
T1=250C
![]()
T2=400C
![]()
Szybkość reakcji wyliczam podstawiając do wzoru kolejno każdą otrzymaną wartość. Następnie kreślę wykres obrazujący zależność zmian stężenia w czasie. Ponieważ zależność jest liniowa wartość nachylenia prostej będzie odpowiadała wartości stałej szybkości reakcji stąd:
k1= 0,0002 dm3/(mol.min) = 0,000003 dm3/(mol.s)
k2= 0,0009 dm3/(mol.min) = 0,000015 dm3/(mol.s)
Energie aktywacji wyznaczam ze wzoru (*)
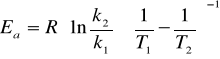
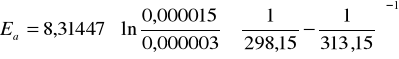
Ea = 77839,6 J/mol
Ea = 77,839 kJ/mol
Wnioski
Podczas doświadczenia badałam stałą szybkości reakcji jodowania acetonu w dwu różnych temperaturach (298,15 K i 313,15 K). Wartości tych stałych wynoszą odpowiednio: k1 = 0,000003 dm3/(mol.s) k2 = 0,000015 dm3/(mol.s)
Wartości te zgadzają się z regułą, że stała szybkości reakcji rośnie wraz ze wzrostem temperatury (wynika to z prawa Arrheniusa).
Biorąc pod uwagę stałe szybkości reakcji w dwu różnych temperaturach obliczyłam energię aktywacji dla reakcji jodowania acetonu, wyniosła ona: Ea = 77,839 kJ/mol.
Analizując wykresy mogę stwierdzić, że oznaczone w trakcie doświadczenia stężenia jodu bardzo dobrze obrazują zależność liniową, a więc co za tym idzie i wyznaczone wartości stałych szybkości oraz energii aktywacji reakcji są dobrym przybliżeniem ich wartości rzeczywistych.
4
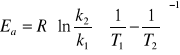
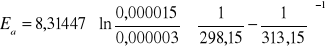
Wyszukiwarka