Promieniowanie temperaturowe. Rozkład natężenia promieniowania źródła w funkcji temperatury (sprawdzenie prawa Wiena)
Wstęp:
Najbardziej powszechną w przyrodzie formą promieniowania elektromagnetycznego jest promieniowanie temperaturowe. Emisja promieniowania temperaturowego zachodzi kosztem energii ruchu cieplnego atomów oraz cząsteczek dowolnego ciała. Inne rodzaje promieniowania emitowanego przez ciała nazywa się luminescencją. Jest ona wynikiem wzbudzenia atomów lub cząsteczek kosztem energii: chemicznej, elektrycznej, mechanicznej, świetlnej lub innej energii wzbudzającej.
W celu wyprowadzenia ilościowych zależności zachodzących w przypadku promieniowania temperaturowego wprowadzono pojęcie ciała doskonale czarnego oraz promieniowania zrównoważonego. Przez ciało doskonale czarne rozumie się takie ciało, które w każdej temperaturze T>0 pochłania wszelkie padające nań (niezależnie od kąta) promieniowanie o dowolnej długości fali λ. Promieniowanie zrównoważone występuje wtedy, gdy odizolowana termicznie grupa nie stykających się ciał ma jednakową temperaturę T. Wynika z tego, że ilość wyemitowanej energii przez dowolne z tych ciał równa się ilości energii zaabsorbowanej. Promieniowanie zrównoważone charakteryzuje się następującymi właściwościami:
- pole promieniowania zrównoważonego jest jednorodne,
- pole promieniowania zrównoważonego jest izotropowe,
- promieniowanie zrównoważone nie jest spolaryzowane.
Energia promieniowania, które pada na dane ciało, może być przez nie pochłonięta, odbita lub przepuszczona.
Jeżeli z całej ergi E część Ea zostaje pochłonięta, część Eσ odbita, część Eρ przepuszczona, to spełniona musi być równość:
E = Ea + Eσ +Eρ
Dla promieniowania zrównoważonego stosunek zdolności emisyjnej ciała do jego zdolności absorpcyjnej równa się natężeniu promieniowania zrównoważonego ciała doskonale czarnego:
Zależność ta nosi nazwę prawa Kirchhoffa. Z prawa Kirchhoffa wynikają trzy ważne wnioski.
1. Zdolność emisyjna dowolnego ciała w danej temperaturze równa jest iloczynowi jego zdolności absorpcyjnej i zdolności emisyjnej ciała doskonale czarnego o tej samej temperaturze:
2. Zdolność emisyjna dowolnego ciała jest mniejsza od zdolności emisyjnej ciała doskonale czarnego o tej samej temperaturze.
3. Jeżeli ciało w jakiejś temperaturze emituje promieniowanie o określonej długości fali, to musi ono również pochłaniać promieniowanie o tej samej długości fali. Nie można jednak tego twierdzenia odwrócić. Z równania wynika, że jeżeli E (λ, T) = 0, to i e (λ, T) = 0, mimo że a (λ, T) = 0. Pochłonięta energia może być zużyta np. na procesy chemiczne, wywołanie zjawiska fotoelektrycznego, jonizację itp.
STEFAN i BOLTZMANN wykazali, że ilość energii E wypromieniowanej w jednostce czasu przez jednostkową powierzchnie S ciała doskonale czarnego w całą półprzestrzeń (dla kąta bryłowego 2π) w funkcji temperatury T jest określona wyrażeniem:
E=δ T4
gdzie:
δ - stała Stefana-Boltzmanna = 5.75 10-8[W/m2K4]
Dla każdego innego ciała promieniującego (rzeczywistego) należy uwzględnić współczynnik emisji e tego ciała, aby określić ilość wypromieniowanej energii:
E = δ e T4
LAMBERT wykazał, że istnieje zależność rozkładu tej energii od kierunku
promieniowania. Matematycznym wyrazem prawa Lamberta jest wzór:
E=E ncosφ
gdzie:
En− energia wypromieniowana wzdłuż normalnej do powierzchni
promieniującej,
φ - kąt miedzy normalną a kierunkiem, w którym określa się ten rozkład.
Prawo to mówi, że ilość energii wypromieniowanej w kierunku tworzącym kąt φ z normalną do płaszczyzny promieniującej jest równa iloczynowi energii En wypromieniowanej w kierunku normalnej i wartości cosinusa kąta φ. Prawo to jest ściśle spełnione dla ciał doskonale czarnych. W przypadku tzw. ciał szarych można je stosować do ciał o powierzchniach nie polerowanych w zakresie zmian kąta φ od wartości 0 do 60°.
Z doświadczenia wynika, że rozkład energetyczny źródła promieniowania jest funkcją długości fali λ i temperatury T danego ciała. Wien wykazał, że zachodzi ścisła współzależność pomiędzy temperaturą T ciała a długością fali
λ w maksimum natężenia promieniowania:
Prawo to można wyrazić przez częstotliwość promieniowania:
Obie te zależności są przedstawione na rysunkach
Wyniki:
λ |
Iż= 2,6 [A] |
Iż= 3 [A] |
Iż= 4 [A] |
700 |
0 |
0 |
0 |
720 |
0,007 |
0,013 |
0,034 |
740 |
0,016 |
0,033 |
0,092 |
760 |
0,032 |
0,067 |
0,195 |
780 |
0,055 |
0,116 |
0,331 |
800 |
0,085 |
0,176 |
0,493 |
820 |
0,116 |
0,24 |
0,661 |
840 |
0,151 |
0,311 |
0,835 |
860 |
0,189 |
0,377 |
1,004 |
880 |
0,226 |
0,45 |
1,16 |
900 |
0,263 |
0,516 |
1,297 |
920 |
0,299 |
0,578 |
1,432 |
940 |
0,332 |
0,634 |
1,537 |
960 |
0,364 |
0,685 |
1,636 |
980 |
0,394 |
0,736 |
1,724 |
1000 |
0,425 |
0,778 |
1,799 |
1020 |
0,451 |
0,819 |
1,858 |
1040 |
0,474 |
0,854 |
1,902 |
1060 |
0,498 |
0,884 |
1,94 |
1080 |
0,518 |
0,91 |
1,964 |
1100 |
0,525 |
0,913 |
1,939 |
1120 |
0,512 |
0,88 |
1,844 |
1140 |
0,494 |
0,841 |
1,73 |
1160 |
0,499 |
0,839 |
1,71 |
1180 |
0,523 |
0,877 |
1,764 |
1200 |
0,547 |
0,905 |
1,812 |
1225 |
0,561 |
0,922 |
1,821 |
1250 |
0,564 |
0,918 |
1,792 |
1275 |
0,559 |
0,903 |
1,742 |
1300 |
0,552 |
0,883 |
1,685 |
1325 |
0,539 |
0,856 |
1,611 |
1350 |
0,526 |
0,83 |
1,546 |
1375 |
0,505 |
0,792 |
1,455 |
1400 |
0,489 |
0,763 |
1,393 |
1425 |
0,466 |
0,717 |
1,291 |
1450 |
0,447 |
0,685 |
1,22 |
1475 |
0,419 |
0,639 |
1,119 |
1500 |
0,399 |
0,604 |
1,042 |
1525 |
0,36 |
0,539 |
0,914 |
1550 |
0,333 |
0,496 |
0,825 |
1575 |
0,302 |
0,445 |
0,724 |
1600 |
0,291 |
0,424 |
0,68 |
1625 |
0,279 |
0,402 |
0,634 |
1650 |
0,273 |
0,391 |
0,61 |
1675 |
0,261 |
0,373 |
0,573 |
1700 |
0,251 |
0,358 |
0,54 |
1725 |
0,234 |
0,328 |
0,484 |
1750 |
0,223 |
0,312 |
0,449 |
1775 |
0,207 |
0,284 |
0,4 |
1800 |
0,197 |
0,267 |
0,366 |
Obliczenia temperatury dla maksymalnego natężenia długości fali:
Iź |
λE max(nm) |
T(K) |
ΔT |
2,6 [A] |
1270 |
2275 |
35 |
3 [A] |
1260 |
2293 |
36 |
4 [A] |
1080 |
2675 |
49 |
Wzory:
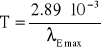
Rozkład Plancka
h = 6,63*10-36
k = 1,38*10-23
c = 2,7*1025
![]()
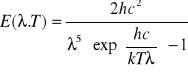
nm] |
[m] |
E |
Dzielnik energii |
Wartości energii do wykresu |
E |
700 |
7E-07 |
3,47E+19 |
1E+18 |
34,726 |
0,52154 |
720 |
7,2E-07 |
3,84E+19 |
1E+18 |
38,434 |
0,52153 |
740 |
7,4E-07 |
4,21E+19 |
1E+18 |
42,147 |
0,52156 |
760 |
7,6E-07 |
4,58E+19 |
1E+18 |
45,832 |
0,52161 |
780 |
7,8E-07 |
4,95E+19 |
1E+18 |
49,459 |
0,52183 |
800 |
8E-07 |
5,3E+19 |
1E+18 |
53,000 |
0,52198 |
820 |
8,2E-07 |
5,64E+19 |
1E+18 |
56,433 |
0,52222 |
840 |
8,4E-07 |
5,97E+19 |
1E+18 |
59,736 |
0,52247 |
860 |
8,6E-07 |
6,29E+19 |
1E+18 |
62,892 |
0,5228 |
880 |
8,8E-07 |
6,59E+19 |
1E+18 |
65,888 |
0,52316 |
900 |
9E-07 |
6,87E+19 |
1E+18 |
68,711 |
0,52357 |
920 |
9,2E-07 |
7,14E+19 |
1E+18 |
71,354 |
0,52396 |
940 |
9,4E-07 |
7,38E+19 |
1E+18 |
73,811 |
0,52434 |
960 |
9,6E-07 |
7,61E+19 |
1E+18 |
76,078 |
0,52481 |
980 |
9,8E-07 |
7,82E+19 |
1E+18 |
78,154 |
0,5251 |
1000 |
0,000001 |
8E+19 |
1E+18 |
80,039 |
0,52561 |
1020 |
1,02E-06 |
8,17E+19 |
1E+18 |
81,735 |
0,5259 |
1040 |
1,04E-06 |
8,32E+19 |
1E+18 |
83,246 |
0,5264 |
1060 |
1,06E-06 |
8,46E+19 |
1E+18 |
84,575 |
0,52685 |
1080 |
1,08E-06 |
8,57E+19 |
1E+18 |
85,729 |
0,5272 |
1100 |
1,1E-06 |
8,67E+19 |
1E+18 |
86,712 |
0,5275 |
1120 |
1,12E-06 |
8,75E+19 |
1E+18 |
87,533 |
0,52678 |
1140 |
1,14E-06 |
8,82E+19 |
1E+18 |
88,197 |
0,52692 |
1160 |
1,16E-06 |
8,87E+19 |
1E+18 |
88,713 |
0,52769 |
1180 |
1,18E-06 |
8,91E+19 |
1E+18 |
89,087 |
0,52815 |
1200 |
1,2E-06 |
8,93E+19 |
1E+18 |
89,328 |
0,52854 |
1225 |
1,23E-06 |
8,95E+19 |
1E+18 |
89,454 |
0,5288 |
1250 |
1,25E-06 |
8,94E+19 |
1E+18 |
89,398 |
0,52894 |
1275 |
1,28E-06 |
8,92E+19 |
1E+18 |
89,176 |
0,52907 |
1300 |
1,3E-06 |
8,88E+19 |
1E+18 |
88,802 |
0,52913 |
1325 |
1,33E-06 |
8,83E+19 |
1E+18 |
88,290 |
0,5291 |
1350 |
1,35E-06 |
8,77E+19 |
1E+18 |
87,653 |
0,5288 |
1375 |
1,38E-06 |
8,69E+19 |
1E+18 |
86,904 |
0,52868 |
1400 |
1,4E-06 |
8,61E+19 |
1E+18 |
86,054 |
0,52851 |
1425 |
1,43E-06 |
8,51E+19 |
1E+18 |
85,116 |
0,52831 |
1450 |
1,45E-06 |
8,41E+19 |
1E+18 |
84,098 |
0,52685 |
1475 |
1,48E-06 |
8,3E+19 |
1E+18 |
83,012 |
0,52685 |
1500 |
1,5E-06 |
8,19E+19 |
1E+18 |
81,866 |
0,5272 |
1525 |
1,53E-06 |
8,07E+19 |
1E+18 |
80,669 |
0,5275 |
1550 |
1,55E-06 |
7,94E+19 |
1E+18 |
79,429 |
0,52678 |
1575 |
1,58E-06 |
7,82E+19 |
1E+18 |
78,152 |
0,52692 |
1600 |
1,6E-06 |
7,68E+19 |
1E+18 |
76,846 |
0,52769 |
1625 |
1,63E-06 |
7,55E+19 |
1E+18 |
75,516 |
0,52815 |
1650 |
1,65E-06 |
7,42E+19 |
1E+18 |
74,168 |
0,52854 |
1675 |
1,68E-06 |
7,28E+19 |
1E+18 |
72,806 |
0,5288 |
1700 |
1,7E-06 |
7,14E+19 |
1E+18 |
71,436 |
0,52894 |
Rachunek błędu:
Błąd dla rozkładu Plancka
![]()
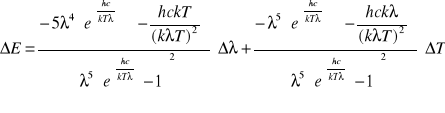
Wyniki obliczeń w tabelce po wyżej
Błędy dotyczące odczytu z przyrządów:
Δ nm]
ΔI=0,001 [A]
Wzór do obliczenia błędu temperatury:
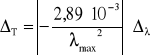
Wyszukiwarka