Połączenia spawane
Połączenia spawane - służą do połączenia w całość elementów maszyn. Można je podzielić na:
ruchowe - umożliwiają względny ruch elementów
spoczynkowe - brak możliwości uwzględnienia ruchu:
nierozłączne - przy próbie demontażu występuje uszkodzenie kształtu przynajmniej jednego elementu połączenia:
bezpośrednie - połączenia spawane, zgrzewane, lutowane, klejone
pośrednie - poprzez użycie łącznika - nitu
rozłączne - można demontować bez uszkodzenia elementów.
Połączenia spawane - zalety:
umożliwiają wykonanie wytworów o złożonych kształtach z prostych części składowych;
można łączyć w całość półwyroby.
Budowa spoiny:
spoina - struktura spoiny ma budowę krystaliczną materiału lanego(zbliżony do staliwa). Struktura ta nie jest zbyt korzystna, dlatego można stosować obróbkę (młotkowanie). W obszarze spoiny występuje nierównomierny rozkład temperatur, co powoduje nierównomierne odkształcenia i naprężenia własne (poważne wady połączeń spawanych)
lico spoiny
strefa wpływów cieplnych
wtop
grań
rąbek
Rodzaje spawania: gazowe, elektryczne, termitowe(szyny kolejowe).
Rodzaje spoin i złączy spawanych:
ze względu na wzajemne usytuowanie łączonych części:
w zależności od usytuowania spoiny w stosunku działania siły:
rodzaje spoin: czołowe, pachwinowe, brzeżne, otworowe.
Grubość spoiny pachwinowej - wysokość trójkąta równoramiennego wpisanego w przekrój poprzeczny spoiny (dla cienkich materiałów: 0.7 grubości materiału).
Rola spoin:
spoiny nośne - przenoszą obciążenia
spoiny pomocnicze:
szczepne - ustalają wzajemne położenie elementów
naprawcze - warstwy naprawcze
uszczelniające - zapewniają szczelność
Spoiny czołowe - stosowane do łączenia blach (unikać łączenia kształtowników walcowanych poddanych rozciąganiu). Lico spoiny powinno być lekko wypukłe, powinno mieć łagodne przejście do materiału rodzimego.
Spoiny pachwinowe - bardzo często stosowane, nie wymagają obróbki łączonych części spoiny.
Obliczenia wytrzymałości spoin:
naprężenia normalne
naprężenia styczne
naprężenia dopuszczalne ze względu na rozciąganie
Zalety łożysk tocznych w odniesieniu do łożysk ślizgowych:
mniejszy współ. tarcia;
statyczny współ. tarcia nieznacznie większy od kinetycznego;
mała wrażliwość na rodzaj środka smarowania;
mała ilość środka smarowego wymagana do poprawnej pracy;
duża sztywność i małe odkształcenia pod wpływem obciążenia;
łożysko, poza specjalnymi przypadkami, pracuje bez odrębnego układu smarowania;
zmiana warunków pracy;
łożyska toczne małych i średnich rozmiarów są tańsze od podobnych łożysk ślizgowych;
prosty montaż i demontaż łożyskowania;
Wady łożysk tocznych:
nie tłumią drgań i przenoszą je na korpus maszyny;
powodują większy szum niż łożyska ślizgowe;
pracują gorzej od łożysk ślizgowych w warunkach dużych przyśpieszeń koszyka;
wysoka cena dużych rozmiarów łożysk;
niepodzielność w płaszczyźnie osi;
większy wymiar w kierunku poprzecznym w stosunku do osi ślizgowych;
Budowa łożysk tocznych:
pierścień zewnętrzny;
pierścień wewnętrzny;
koszyk - oddziela elementy toczne w celu uniknięcia wzajemnego tarcia; rozmieszcza je równomiernie po obwodzie i prowadzi te elementy utrzymuje łożysko jako zwartą całość;
element toczny;
bieżnie główne - przenoszą obciążenie głównym kierunku działania łożyska;
bieżnie pomocnicze - prowadzą elementy toczne lub przenoszą obciążenie w kierunku innym niż główny.
Materiały stosowane na łożyska:
części toczne i pierścienie - wykonuje się ze stali chromowej i hartuje się do twardości 59 - 65 HRC, czasami elementy wykonuje się ze stali do nawęglania;
powierzchnie robocze - są szlifowane i dogładzane oscylacyjnie;
kulki - są docierane;
powierzchnie montażowe - są szlifowane, a w wykonaniu dokładnym - docierane;
Klasyfikacja łożysk:
normalny kąt działanie łożysk - zawiera się między prostą łączącą punkty styku bieżni z kulkami w nieobciążonym łożysku a płaszczyzną prostopadłą do osi łożyska; w łożyskach wałeczkowych jest to kąt pomiędzy prostą łączącą punkty styku bieżni z kulkami w nieobciążonym łożysku a płaszczyzną prostopadłą do tworzącej bieżni zewnętrznej ;
kształt części tocznych:
możliwość wzajemnego wychylenia się pierścieni:
łożyska zwykłe - wymagają zachowania z odpowiednią dokładnością współosiowości wału i oprawy;
łożyska wahliwe - pozwalają na stałą lub zmienną w czasie nie współosiowość
łożyska samonośne - pozwalają na pracę przy stałej, dużej nie współosiowości
Obliczanie łożysk:
nośność ruchowa C - obciążenie, przy którym łożysko osiągnie nominalną trwałość 1 miliona obrotów:
ł. poprzeczne - obciążenie działające w płaszczyźnie prostopadłej do osi łożyska;
ł. wzdłużne - obciążenie działające w płaszczyźnie równoległej do osi łożyska;
nośność spoczynkowa C0 - wielkość obciążenia pod działaniem którego całkowite, trwałe odkształcenie części tocznych i bieżni w miejscu najbardziej obciążonym wymości: 0,0001 średnicy części tocznej:
trwałość normalna 1mln. obrotów L10 - po wykonaniu 1mln. obrotów ulegnie uszkodzeniu nie więcej niż 10% dużej partii badanych łożysk.
równanie trwałości:
Trwałość i nośność techniczna:
Linia śrubowa walcowa prosta - jest o tor punktu M wykonującego ruch obrotowy w płaszczyźnie P przesuwającej się w kierunku prostopadłym do P'. Może być prawo lub lewo skrętna.
Tworząca gwintu - jest to odcinek (krzywa) dowolnego kształtu i rozmiaru, nie tworząca pętli o krańcowych punktach, leżących na prostej równoległej walca OK. i są położone we wzajemnej odległości h. Tworząc gwintu opisuje powierzchnię gwintową, wykonując ruch śrubowy, w którym każdy z jej punktów opisuje linię śrubową.
Rodzaje gwintu:
trójkątny:
trapezowy symetryczny:
trapezowy niesymetryczny:
prostokątny:
okrągły:
zewnętrzny - mierzony na zewnątrz walca;
wewnętrzny - mierzony wewnątrz otworu.
Kąt rozwarci gwintu α - jeśli dwusieczna kąta α tworzy z osią gwintu kat prosty, to gwint jest symetryczny, inaczej gwint jest niesymetryczny.
Wielkości charakteryzujące gwint:
tg - rzeczywista głębokość gwintu;
tn =( tg - a) - nośna głębokość gwintu;
a - luz wierzchołkowy;
dr - średnica rdzenia śruby;
dp - średnica podziałowa śruby;
d - średnica zew. Śruby równa średnicy nominalnej;
D0 - średnica otworu nakrętki;
Dp - średnica podziałowa nakrętki;
D - średnica nakrętki;
ds. - średnica robocza:
tgγ - tangens średnicy kąta pochylenia gwintu:
Zastosowanie gwintu:
główne cechy gwintu:
kąt rozwarcia α
promień zaokrąglenia r
gwinty metryczne, zwykłe, drobnozwojowe: α = 60°; r = 0,1082h;
gwinty calowe: α = 55°; r = 0,13733h;
gwinty trapezowe niesymetryczne: α = 3° (kat powierzchni roboczej) ;
=30 ° (kąt powierzchni pomocniczej);
gwint płaski - wychodzi z użycia z powodu trudności wykonawczych i małej wytrzymałości co do gwintu trapezowego;
gwint drobnozwojowy - stosowany w celu małej głębokości gwintu;
gwint okrągły - stosowany jako łącznik narożny na zmienne obciążenie; stosowany w połączeniach między wagonowych;
gwint trapezowy - połączenia ruchowe, jeżeli zależy na wysokiej sprawności to stosuje się gwinty trapezowe wysoko zwojowe;
gwint stożkowy - do rurociągów wiertniczych; dają dobrą szczelność złącza; likwidują luzy; zapewniają równomierność obciążenia na poszczególnych zwojach; krótki czas montażu.
Połączenia śrubowe:
spoczynkowe - złącza kołnierzowe;
ruchowe - wrzeciono zaworu, śruba pociągowa obrabiarki.
Warunek samohamowności:
Sprawność połączenia gwintowego:
Rodzaje pasów w przekładni pasowej ciernej:
płaski
klinowy
okrągły.
Zalety przekładni pasowych:
płynność ruchu;
cichobieżność;
zdolność do łagodzenia zmian obciążenia;
tłumienie drgań;
prosta i tania konstrukcja;
praca beż smarowania;
możliwość przenoszenia ruchu gdy wały nie są równoległe.
Wady przekładni pasowych:
stosunkowo duże wymiary;
duża siła na łożyskach wałów;
niestałość przełożenia z powodu poślizgu;
mała odporność na podwyższoną temperaturę (chodzi o pas);
mniejsza sprawność w porównaniu z przekładnią zębatą i łańcuchową - 90%.
Rodzaje przekładni pasowych ze względu na układ osi wału:
skrzyżowana;
półskrzyżowana;
półskrzyżowana z krążkiem kierującym;
półskrzyżowana z dwoma krążkami kierującymi;
otwarta z dwoma krążkami kierującymi;
otwarta z jednym krążkiem kierującym I napinającym.
Sposoby napinania pasa:
pod jego ciężarem własnym;
poprzez rolkę naprężającą;
poprzez okresowe przesuwanie silnika na podstawie;
poprzez odchylenie silnika.
Moc przekładni pasowych:
użyteczne napięcie pasa:
prędkość liniowa pasa:
Wyznaczanie długości pasa:
kąt opasania pasa styka się z kołem pasowym:
Napięcia w cięgnach i obciążenie wałów:
siła użyteczna:
siła obciążenia wału jest równa wypadkowej pochodzącej od nacisku pasa na koło; jest równa sumie geometrycznej napięć w cięgnach:
odległość między siłami Q:
Kinetyka przekładni pasowej:
poślizg sprężysty - różnica prędkości obu cięgien do prędkości cięgna roboczego:
Współczynnik napięcia pasa:
Przekładnie pasowe klinowe:
formowy współczynnik tarcia:
minimalna odległość osi:
Kolejność obliczeń przekładni:
wybór typu wielkości pasa klinowego (zależy od prędkości obrotowej i przenoszonej mocy);
przyjęcie średnicy skutecznej małego koła;
sprawdzenie prędkości liniowej pasa wg. wzoru;
obliczenie średnicy skutecznej dużego koła:
przyjęcie orientacyjne rozstawu osi koła;
wyznaczenie kata opasania koła małego:
obliczenie długości pasa:
sprawdzenie częstotliwości zginania pasa:
obliczenie liczby pasów klinowych:
Przekładni pasowe z pasem zębatym:
z dwoma kołami uzębionymi;
z dużym kołem o gładkiej powierzchni;
z dwustronnym uzębieniem.
Rodzaje kołków:
stożkowy - działa środkujaco i nadaje się do połączeń często rozłanczalnych; droga luzowania jest krótka, małe zużycie; otwór na ten kołek powinien być rozwiercony po złożeniu łączonych części.
stożkowy z gwintem - stosowany w przypadku ślepych otworów, ponieważ daje się wyjąć z otworu poprzez wkręcenie nakrętki na gwint.
cylindryczny - wymaga pasowania ruchowego i wysokiej klasy dokładności wykonania otworu; droga luzowania długa, zużycie duże; nie nadaje się do wielokrotnego demontażu; wykonanie połączenia jest kosztowne.
sprężynujący rurowy - wykonany ze stali sprężynowej, nie wymaga rozwierconego otworu, bywa również używany w połączeniach śrubowych jako tuleje odciążająca śrubę od ściskania.
Połączenia kołkowe-czopowe - stosowane do celów podrzędnych; otwór na kołek osłabia wał; wymiary przyjmuje się w stosunku czopa Dc - średnica czopa.
Połączenia kołkowe - czopowe podłużne - stosowane do osadzenia piasty na końcu wału.
Połączenia sworzniowe:
rodzaje sworzni:
ciasno pasowane w otwór;
luźno pasowane w otwór;
Połączenia wpustowe - wpust jest osadzony z wcięciem we wzdłużnym rowku wykonanym w czopie i występuje ponad powierzchnię czopa i piasty. Połączenie posiada luz powierzchniowy pomiędzy dnem rowka w piaście i wpustem. Kształty i wymiary są znormalizowane. Przekrój poprzeczny wpustu jest prostokątny a jego wymiary zależą od średnicy czopa. Długość wpusty może być zmienna i jest ustalona przez konstruktora.
rodzaje połączeń wpustowych:
spoczynkowe - wpust jest ciasno pasany w rowku i w piaście;
przesuwne - wpust jest ciasno pasowany w rowku wału i luźno pasowany w piaście.
Połączenia wielowypustowe - rodzaje:
o prostych zarysach boków;
wielokarbowe;
o zarysach ewolwentowych.
Połączenia klinowe wzdłużne - podobne do połączeń wpustowych; wpust zastąpiono klinem o zbieżności 1-100. poprzez wbicie klina w złączu powstają naprężenia. Klinów nie oblicza się wytrzymałościowo; długość klina można orientacyjnie określić ( jak dla wpustu).
Wykres Haygha:
Punkt A na osi σa określa granicę zmęczenia przy obciążeniu wahadłowym.
Pkt. B na osi σm określa w przybliżeniu wytrzymałość przy obciążeniu statycznym czyli Rm.
Dla materiałów elastooptycznych wprowadza się warunek σmax = σm+σa ≤ Re warunek ten określa położenie lini ograniczającej, która łączy wartości Re na obydwu osiach.
Zjawiska zmęczenia w metalach i ich przebieg:
powstanie i rozwój lokalnych odkształceń plastycznych oraz związanego z nimi lokalnego przejściowego umocnienia i osłabienia
powstanie mikropęknięć
rozwój i łączenie się pęknięć aż do całkowitej dekoezji (zniszczenia)
Czynniki wpływające na wytrzymałość zmęczeniową:
działanie karbu - w miejscu zmian kształtu lub wymiaru obciążonego detalu występuje zmiana rozkładu naprężeń, naprężenia zmieniają się (mówimy o działaniu karbu).
karbem są : odsadzenia, rowki, otwory, wcięcia, gwinty.
karby są przyczyną 33% uszkodzeń części maszynowych .
naprężenie nominalne σn wyznaczamy z zależności:
Mg-moment gnący
Wx- wskaźnik przekroju na zginanie (dla najmniejszego przekroju karbu)
Współczynnik kształtu (teoretyczny współczynnik działania karbu)
Współczynnik działania karbu:
współczynnik β k określa wielkość zmniejszenia wytrzymałości zmęczeniowej na skutek działania karbu i jest równy stosunkowi wytrzymałości zmęczeniowej
współczynnik β k można wyznaczyć doświadczalnie dla ograniczonej liczby przypadków. Wg jednej z koncepcji p.Thuma, Buchmana, Petersona, £k i βk łączy współczynnik wrażliwości materiału na działanie karbu:
współczynnik η k możemy odczytać z wykresu funkcji zależności współczynnika kształtu £ k i współczynnika wrażliwości η k .
Rodzaje karbu:
karb wielokrotny - kilka występujących obok siebie karbów. Może mieć to działanie wzmacniające lub osłabiające (odciążające i przeciążające).
karby szeregowe - są to karby odciążające
karby równoległe - są to karby przeciążające
Zmniejszenie wpływu karbu przez konstrukcyjne kształtowanie.
należy unikać sytuacji aby stosunek promienie karbu ρ do 2r był ≤ 0,1.
odsadzenia warto umacniać poprzez ulepszenia cieplne lub dogniatanie.
Wpływ wielkości przedmiotu:
wytrzymałość zmęczeniowa na ogół maleje wraz ze wzrostem wymiaru elementu. Brak jest dostatecznego teoretycznego wyjaśnienia tego zjawiska. Wpływ ten opisuje się najczęściej probalistycznie na zasadzie prawdopodobieństwa wystąpienia najsłabszego ogniwa.
wielkość przedmiotu ma największy wpływ na wytrzymałość zmęczeniową przy zginaniu i skręcaniu, a znacznie mniejszy przy rozciąganiu i ściskaniu.
wpływ w przedmiocie ujawnia się silniej w zakresie granicznej wytrzymałości zmęczeniowej. Ze wzrostem średnicy rośnie również rozrzut wartości współczynnika ∑.
Wpływ rodzaju obróbki i stanu warstwy wierzchniej βp.
Obróbki polepszające warstwę wierzchnią.
obróbka cieplna, płytkie hartowanie, azotowanie, węglownie i hartowanie.
Obliczanie współczynnika bezpieczeństwa:
dla cykli symetrycznych:
Rzeczywisty współ. bezpieczeństwa δ (współ. niewiedzy), dla cykli symetrycznych
W obliczeniach wstępnych pomocna jest znajomość naprężeń dopuszczalnych, wyznaczonych na podstawie granicy zmęczenia dla danego rodzaju obciążenia i współczynnika XZ, który obejmuje współczynniki: δ, ξ, β:
zginanie wahadłowe kg0:
Wyznaczanie obciążeń złożonych - korzystamy z hipotezy Haygha:
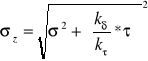
Rzeczywisty współczynnik bezpieczeństwa δ:
Wałem lub osią - nazywamy element maszyny, na którym są osadzone inne elementy wykonujące ruchy obrotowe lub oscylacyjne. Wał lub oś urzeczywistnia ich geometryczną oś obrotu. Wał - służy głównie do przenoszenia momentu obrotowego. Za jego pośrednictwem przenoszone są na łożyska obciążenia działające na elementy na nim osadzone. Wał poza skręcaniem narażony jest głównie na zginanie, skręcanie i rozciąganie. Oś - nie przenosi momentu obrotowego, jest obciążona głównie momentem gnącym. Służy do utrzymywania zadanym położeniu innych obracających się elementów maszyny. Osie mogą być: ruchome - oś obraca się wraz z elementami na niej osadzonymi; stałe - oś utwierdzona jest nieruchomo w uchwytach zaś inne elementy są na niej łożyskowane i mają możliwość obrotu. Sworzniem - nazywamy krótką oś. Czopami - mogą być części wałów lub osi, na których występuje styk z innymi elementami maszyny.
Podział wałów i osi:
Dobór materiału na wały:
stale zwykłej jakości;
stale wyższej jakości - odpowiednie wały maszynowe do temper. 750K;
stale do ulepszania cieplnego - przy silnych obciążeniach udarowych;
stale do nawęglania;
stale 26H2MF, 25HM - w temper. do 810K;
stale H25, M25, S2 - w temper. wysokich, do 1020K.
Obliczenia wałów wyłącznie skręcanych:
prędkość obrotowa wału;
moment obrotowy przenoszony przez wał;
dla wałów płaskich o długości l należy sprawdzić:
naprężenia:
kąt skręcenia wału ϕ:
jednostkowy kąt skręcenia ϕ':
dla wałów kształtowych (o różnych średnicach):
kąt skręcenia ϕ:
jednostkowy kąt skręcenia ϕ'':
W celu złagodzenia momentu skręcającego stosuje się wałki skrętne, które łagodzą nierównomierność przenoszonego momentu:
Obliczenia wałów narażonych na zginanie i skręcanie:
naprężenia dopuszczalne:
naprężenia styczne:
naprężenia zastępcze:
moment zastępczy przy zginaniu:
wyznaczenie średnicy wału przy zginaniu i skręcaniu:
Obliczenia osi przeprowadza się przy założeniu stałych wartości obciążeń. Jeżeli obciążenie jest zmienne to do obliczeń przyjmuje się maksymalne ich wartości.
doczołowe, teowe, narożne, przylgowe, zakładkowe, krzyżowe;
poprzeczne, podłużne, skośne;
Spoinę pachwinową - sprawdza się na warunek naprężeń niebezpiecznych. W przypadku spoin sprawdza się warunki na:
![]()
Q - obciążenie, F - wskaźnik przekroju (wskaźnik momentu)
![]()
P - siła, kst' - obciążenie statyczne (napięcie dopuszczalne dla spoiny)
![]()
s - współ. zależny od rodzaju obciążenia: 0.8 - rozciąganie; 1 - ściskanie; 0.9 - zginanie;
0.65 - ścinanie;
s0 - współ. jakości spoiny: 1 - spoina przebadana; 0.5 - bez badania;
![]()
Re - granica plastyczności, Xe - współ. bezpieczeństwa (1.6 - w układach bez
obciążenia sprężysto - plastycznego)
Łożyska toczne
- kulkowe; - walcowa; - igiełkowe; -stożkowe; - baryłkowe;
wału i oprawy;
wału i oprawy;
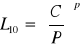
![]()
P - obciążenie zastępcze ruchowe; C - nośność ruchowa; p = 3, 10/3;
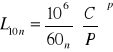
n - prędkość obrotowa [obr/min]
![]()
Fr - skł. poprzeczna obciążenia; Fa - skł. względna obciążenia; XY - współ. przeliczeniowy
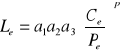
a1 - współ. niezawodności: 0,21 (99%); 0,05 (100%)
a2 - współ. materiałowy
a3 - współ. warunków pracy
Ce - efektywna nośność ruchowa w temper. pracy;
Ce = C*ff
Pe - efektywne obciążenie łożysk;
Pe = fd*P
fd - współ. dynamiczny
Połączenia śrubowe
h - skok wzdłużny linii śrubowej
Punkt M będzie opisywał na płaszczyźnie P spiralę Archimedesa. Wtedy na powierzchni stożka powstanie linia śrubowa stożkowa. Odległość miedzy punktami spirali s - skok poprzeczny linii śrubowej.
hz - podziałka zwoju gwintowego - odległość sąsiednich występów, mierzona na zarysie wzdłuż osi:
h = hz gwint jednokrotny
h - z*hz gwint wielokrotny
Wszystkie wymiary gwintów normalnych są znormalizowane i określone w zależności od podziałki gwintu hz. Średnia Dn dla gwintu zewnętrznego jest równa średnicy śruby. Dn i skok gwintu są ze sobą powiązane. Przy tej samej średnicy zewnętrznej mogą wystąpić różne skoki. Gwinty o skoku mniejszym od skoku gwintu zwykłego nazywane są gwintami drobnozwojowymi, o większym skoku gwintami grubo zwojowymi.
![]()
![]()
ρ > γ
tgγ - tangens średnicy kąta pochylenia gwintu; ρ - kąt tarcia, (ρ = arctgμ, μ = tgγ)
![]()
Lu - praca użyteczna; Lw - praca włożona
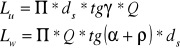
Przekładnie pasowe
Przekładnie pasowe służą do przenoszenia mocy za pośrednictwem cięgien w postaci pasów. Siła tarcia pozwala przenosić siłę obwodową, dzięki tarciu.
![]()
![]()
![]()
d - średnica koła pasowego; n - ilość obrotów.
![]()
![]()
![]()
![]()
μ - współczynnik tarcia; ![]()
α1 - kąt opasania koła małego.
![]()
![]()
![]()
![]()
Vc - cięgno czynne; Vb - cięgno bierne
![]()
![]()
A - pole przekroju poprzecznego pasa; E - moduł sprężystości wzdłużnej pasa;
![]()
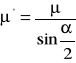
α - kat zarysu
![]()
![]()
![]()
![]()
z - liczba kół zębatych; L - długość pasa.
![]()
P1 - moc dla jednego pasa klinowego; kL - współ. żywotności pasa: 0,72-1,2;
kα - współ. kata opasania: 1-180stopni; kT - współ. trwałości pasa.
Połączenia kołkowe, sworzniowe, klinowe
Połączenia te należą do grupy połączeń kształtowych, których cechą jest równoważenie przenoszonych sił siłami spójności łączników. Względne przemieszczenie elementów głównych w kierunku przeważających sił lub ich względny obrót zgodnie z przenoszonym momentem obrotowym jest możliwy dopiero po zniszczeniu łączników połączenia.
Wytrzymałość zmęczeniowa
Wykres ten otrzymuje się na podstawie badań zmęczenia każdej parze wartości σa i σm dla danego współczynnika asymetrii. Cyklu R odpowiada punkt na wykresie, a połączenie tych pkt. tworzy krzywą.
Proste wychodzące z początku układu pod kątem W są miejscem geometrycznym pkt. o R=const.
TgW=σa/σm=σmax-σmin/σmax+σmin=1-R/1+R
Suma rzędnej i odciętej tego pkt. jest granicą zmęczenia „z” dla danego współczynnika asymetrii R.
σmax=OE+EC=σm
Prosta OD nachylona pod kątem 45o wyznacza na krzywej punkt wskazujący współrzędne do obliczenia granicy zmęczenia przy odzerowo tętniącym obciążeniu.
σm = σa =Zrj/2
Wykres ten obejmuje także zakres σm<0 (jest to symetryczne odbicie prawej części wykresu).
Zjawiska te mimo ich złożoności mają określoną prawidłowość, można wyróżnić 3 etapy:
Przez karb należy rozumieć miejsca zmian poprzecznych przekrojów elementu lub zmiany krzywizn powierzchni ograniczających przedmiot.
Działanie karbu można przedstawić jako miejsce zagęszczenia linii sił, a więc trajektoriom punktów przekazującym obciążenie elementarnym cząstką materiału.
σ n = P / Ak
P- obciążenie
Ak- pole powierzchni
σn =Mg / Wx
£ K = σ max/ σ n
Dla skręcania £ K = τ max / τ n
£ k- jest wielkością związaną wyłącznie z geometrią karbu nie zależy od wielkości obciążenia bezwzględnych wymiarów elementu, rodzaju materiału w stanie sprężystym. Wyznaczamy go doświadczalnie używając tensometrów lub obliczając MES lub MEP.
£ k= ƒ(ρ/r ; R/r ; rdz. obciążenia ;kształt elementu ).
£ k
3
2
1
ρ/r
Działanie karbu w konkretnych elementach konstrukcyjnych jest inne niż w materiałach modelowych o liniowej sprężystości.
Wprowadzono praktyczną miarę wpływu spiętrzenia naprężeń na wytrzymałość zmęczeniową. Miarą tą jest współczynnik działania karbu:
β k - ten współczynnik nazywamy współczynnik karbu, (efektywny współczynnik spiętrzenia naprężeń).
β k= Zgt / Zk
Stosunek próbki gładkiej do wytrzymałości zmęczeniowej próbki z karbem β k ≥ 1.
0 ≤ η k ≤ 1 ηk=βk-1/£k-1 βk=1+ηk(£k-1)
Jeżeli materiał ma dużą wrażliwość na działanie karbu to wtedy η k jest równy 1 i współczynnik £k=βk. Taką własność mają materiały doskonałą sprężystość i doskonale kruche (szkło).
η k= 0 brak wrażliwości na działanie karbu. Własność taką mają materiały doskonale plastyczne (wyjątek: żeliwo szare -> η k ≈ 0).
Ρ/2r ≤ 0,1
∑= Zd / Z
Zd - wytrzymałość zmęczeniowa próbki o dowolnej średnicy
Z - wytrzymałość tego samego materiału o średnicy 7 - 10 mm.
β p=Z/Zp
Z - wytrzymałość zmęczeniowa próbki polerowanej
Zp - wytrzymałość zmęczeniowa po różnej obróbce (innej niż polerowanie)
W przypadku ostrych karbów βp współczynnik ten można ominąć.
Przy karbie łagodnym β=βk+βp=1 (stan powierzchni należy uwzględnić)
Dla żeliwa po usunięciu naskórka odlewniczego β = 1
Zabiegi te znacznie zwiększają granicę zmęczenia zwłaszcza dla elementów z karbem. Chodzi tu o zgniot warstwy wierzchniej powstałej w kulkowaniu, wałeczkowaniu, rozwalcowaniu i wciskaniu stempla.
Powlekanie galwaniczne zmniejsza granicę zmęczenia.
Wpływ tych różnych obróbek uwzględnia współczynnik βpz.
Βpz = Z/Zpz
Z- wytrzymałość zmęczeniowa próbki gładkiej z karbem
Zpz- wytrzymałość zmęczeniowa próbki po różnych zabiegach
Β= β k *βpz
Β=βk+βpz-1
![]()
Z - - granica zmęczenia przy danym rodzaju obciążenia symetrycznego;
σna - nominalna amplituda naprężenia, obliczona zwykłą metodą obliczeniową;
β - współ. działania karbu;
σna = σmax wynosi: 1,3 < δ < 2,5
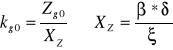
XZ - przyjmuje się: 2,5 - 4.
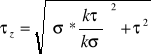
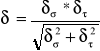
Wały i osie
- gładkie; - kształtowe; - pełne; - drążone (obniżanie masy);
- okrągłe lub profilowe; całkowite lub składane.
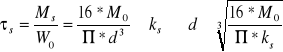
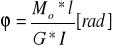
M0 - moment skręcający [N*mm]; G - moduł sprężystości poprzecznej [MPa];
I0 - biegunowy moment bezwładności przekroju [mm4].
![]()
![]()
k - liczba stopni wału; li - długość stopnia wału o średnicy di;
![]()
obciążenie jednostronnie zmienne (skręcanie);
![]()
obciążenie obustronnie zmienne;
![]()
ϕ' > 0,2 [rad/m]
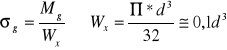
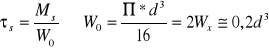
![]()
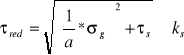
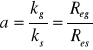
zależności:
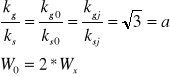
![]()
gdy redukujemy do naprężeń moralnych;
![]()
gdy redukujemy do naprężeń stycznych;
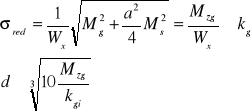
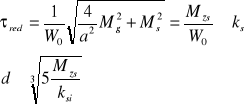
i = o, j: (o - obustronne; j - jednostronne obciążenie.
Podstawy konstrukcji maszyn: Malczewski & Żurawski
σ a
Re
Zrc
Zrj/2
45º
Zrj/2
ω
B
B'
σ m
0
E
D
C
A
0,1
0,2
0,3
R/r=3
2
3
Materiał modelowy
Wyszukiwarka