Elementy logiki matematycznej i algebry zbiorów
Przypomnijmy podstawowe oznaczenia i definicje
Zdaniem w matematyce nazywamy takie zdanie w sensie gramatycznym, o którym można jednoznacznie orzec, czy jest prawdziwe czy fałszywe. Wartość logiczną zdania prawdziwego oznaczamy przez 1, zdanie fałszywe ma wartość logiczną 0.
Definicje: negacji zdania ![]()
, alternatywy zdań p i q ![]()
, koniunkcji ![]()
, implikacji ![]()
i równoważności ![]()
przypominamy skrótowo w poniższych tabelkach:
p |
~ p |
1 0 |
0 1 |
p |
q |
|
|
|
|
1 1 0 0 |
1 0 1 0 |
1 1 1 0 |
1 0 0 0 |
1 0 1 1 |
1 0 0 1 |
Symbole: ![]()
oznaczają odpowiednio kwantyfikator ogólny (czyt. dla każdego) i kwantyfikator szczegółowy (czyt. istnieje).
W dalszym ciągu będziemy również korzystać z następujących oznaczeń i definicji:
N - zbiór liczb naturalnych, N = {1,2,3,........},
C - zbiór liczb całkowitych , całkowitych = {0,-1,1,-2,2,........},
W - zbór liczb wymiernych W = {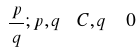
R - zbiór liczb rzeczywistych,
R+ - zbiór liczb rzeczywistych dodatnich,
![]()
- przedział domknięty o końcach a i b,
![]()
- przedział otwarty o końcach a i b, itd.
![]()
- suma mnogościowa zbiorów Ai B,
![]()
- iloczyn mnogościowy zbiorów A i B,
![]()
+ różnica mnogościowa zbiorów A i B.
Zadania
1. Podać wartość logiczną zdań:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) 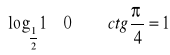
f) Nieprawda, że suma kątów wewnętrznych w trójkącie jest równa ![]()
.
g) Długość okręgu jest mniejsza od długości jego średnicy lub długość okręgu jest większa od długości jego promienia.
h) Suma kątów wewnętrznych w równoległoboku jest równa ![]()
i długość obwodu równoległoboku jest większa od sumy długości jego przekątnych.
i) Jeżeli liczba 8 jest podzielna przez 5, to liczba 8 jest podzielna przez 3.
j) Liczba 3 jest podzielnikiem liczby 7 wtedy i tylko wtedy, gdy liczba 5 jest podzielnikiem liczby 5.
2. Sprawdzić, czy następujące formuły zdaniowe są tautologiami (prawami rachunku zdań):
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
g) ![]()
h) ![]()
i) ![]()
j) ![]()
3. Podać wartości logiczne zdań:
a) 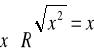
b) 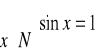
c) 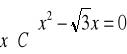
d) 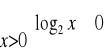
e) ![]()
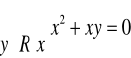
f) ![]()
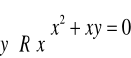
g) ![]()
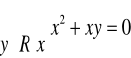
h) ![]()
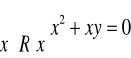
i) ![]()
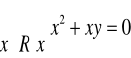
j) ![]()
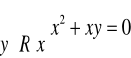
4. Zapisać formalnie poniższe zdania i podać ich wartości logiczne:
a) Równanie ![]()
ma rozwiązanie w zbiorze liczb naturalnych.
b) Dla dowolnych liczb rzeczywistych x, y wartość bezwzględna z ich sumy nie przekracza (jest mniejsza lub równa) od sumy ich wartości bezwzględnych.
bezwzględnych) Dla dowolnych dwóch liczb rzeczywistych pierwsza z nich nie przewyższa (jest mniejsza lub równa) od drugiej lub druga nie przewyższa (jest mniejsza lub równa) od pierwszej.
d) Nie dla każdej liczby rzeczywistej jej kwadrat jest od niej większy.
5. Niech ![]()
, ![]()
Wyznaczyć zbiór B, ustalić relację (równość, inkluzja) między zbiorami A i B i znaleźć ![]()
, ![]()
, ![]()
, ![]()
.
6. Znaleźć ![]()
, ![]()
, ![]()
, ![]()
, jeżeli:
a) ![]()
![]()
b) ![]()
![]()
c) ![]()
![]()
d) ![]()
![]()
Przypomnijmy, że 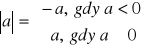
e) A = N
![]()
f) ![]()
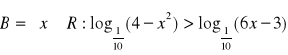
g) ![]()
![]()
h) ![]()
![]()
7. Na płaszczyźnie 0XY dane są zbiory:
a) ![]()
![]()
b) ![]()
![]()
c) ![]()
![]()
Narysować:
![]()
dla a)
![]()
dla b)
![]()
dla c)
8. Niech ![]()
, ![]()
. Dla jakich wartości parametru ![]()
zbiór ![]()
jest zbiorem jednoelementowym? Sporządzić odpowiedni rysunek.
Odpowiedzi
1. Zadania a), b), j) mają wartość logiczną 0 (są fałszywe); pozostałe zdania SA prawdziwe.
2. Formuły h), j) nie są tautologiami; pozostałe formuły są tautologiami.
Wskazówka: najdogodniej zastosować tzw. metodę zero - jedynkową. I tak np. dla g) mamy:
p |
q |
|
|
|
|
|
1 1 0 0 |
0 0 1 1 |
0 0 1 1 |
0 1 0 1 |
1 0 1 1 |
0 0 0 1 |
1 1 1 1 |
Ponieważ w ostatniej kolumnie (zawierającej badaną formułę) występują same jedynki, więc formuła (schemat zdaniowy) jest tautologią.
3. Zdania c), f), g), i), j) mają wartość logiczną 1 (są prawdziwe); pozostałe zdania są fałszywe.
4.
a) 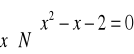
b) 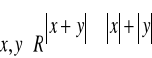
c) 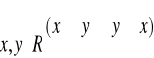
d) 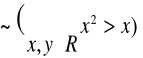
![]()
![]()
![]()
![]()
Wszystkie powyższe zdania są prawdziwe.
Uwaga: w d) wykorzystaliśmy prawo De Morgana dla kwantyfikatorów.
5.
B = {-2,0,2},
![]()
![]()
,
![]()
,
![]()
,
![]()
.
6.
a) ![]()
![]()
,
![]()
,
![]()
.
b) ![]()
,
![]()
![]()
,
![]()
.
c) ![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
.
d) ![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
.
e) ![]()
,
![]()
,
![]()
,
![]()
,
![]()
.
f) ![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
.
g) ![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
.
h) ![]()
,
![]()
![]()
![]()
![]()
![]()
Wskazówka: aby wyznaczyć zbiór A podstawiamy ![]()
. Otrzymujemy nierówność: ![]()
. Stąd otrzymujemy t > 3 czyli ![]()
. Ostatnią nierówność logarytmujemy logarytmem o podstawie 3.
W celu wyznaczenia zbioru B przekształćmy nierówność do postaci:
![]()
W przedziale ![]()
powyższe nierówności można podnieść do kwadratu. W przedziale ![]()
powyższa nierówność jest tożsamością.
7.
a)
b)
c)
8. ![]()
![]()
Wyszukiwarka