Temat: Fale elektromagnetyczne w przezroczystych kryształach niemagnetycznych

Fale płaskie w przezroczystych kryształach niemagnetycznych

Propagację fal elektromagnetycznych w przezroczystych, krystalicznych, dielektrycznych oś­rodkach niemagnetycznych, w których brak ładunku swobodnego, opisują równania Max­wella zależne od wektorów pola elektrycznego E, indukcji magnetycznej D i pola magnetycznego B

(3.1a,b)

(3.1c,d)

Wektory D i E łączy związek liniowy

(3.2)

Niech
będą wartościami własnymi tensora stałych dielektrycznych ε. Wkład pola elektrycznego do gęstości energii wewnętrznej dielektryka jest proporcjonalny do DE i jest wielkością dodatnią

.

To oznacza, że tensor stałych dielektrycznych jest symetrycznym tensorem dodatnim

(3.3a)

. (3.3b)

Spełnienie nierówności (3.3b) gwarantuje istnienie tensora

, (3.3c)

który nosi nazwę tensora przenikalności dielektrycznej.

Jak poprzednio będziemy badać rozchodzenie się elektromagnetycznych fal płaskich o wektorze falowym k i częstości ω w powyższych ośrodkach, a więc

(3.4a-d)

gdzie
Prędkość światła
w ośrodku materialnym różni się od prędkości światła w próżni c. Iloraz
określa współczynnik załamania n

(3.5)

Liczba falowa k, częstość kołowa ω oraz prędkość v spełniają znany związek

(3.6)

Wyrazimy fazę
przez współczynnik załamania n

(3.8)

gdzie m jest wektorem refrakcji

(3.9)

Tak jak poprzednio (por. § 1) dla fal płaskich równania Maxwella (3.1) sprowadzają się do równań algebraicznych, lecz tym razem bardziej skomplikowanych

(3.10a,b)

(3.10c,d)

Wektory
spełniają takie same równania jak
. Łatwo się przekonać, że

(3.11a,b)

natomiast
. Znajdziemy wektor, do którego prostopadły jest wektor E. W tym celu rozpatrzymy warunek (3.10c)

. (3.11c)

Jak widać wektor E jest prostopadły do wektorów H i
(rys. 3.1). W ogólnym przypadku wektor
nie jest równoległy do wektora
.

Wyrugujemy z równania (3.10a) wektor H, w tym celu wykorzystamy tożsamość (1.10b). Wynik wygodnie będzie zapisać w postaci tensorowej

, (3.12a)

gdzie I jest jednostkowym tensorem drugiego rzędu. W dowolnie wybranym układzie współrzędnych tensor I reprezentuje macierz, której elementami są symbole Kroneckera

, (3.13a)

natomiast
jest diadą. Niech u i v będą dwoma dowolnymi, nieznikającymi wektorami. Diada, czyli tensor
ma składowe

(3.13b)

Wykorzystamy związek (3.2). Po wyrażeniu wektora E przez wektor D z równania (3.12a) otrzymamy jednorodny układ równań liniowych

(3.12b)

Równanie (3.12b) pozwala określić współczynniki załamania i polaryzację fal rozchodzących się w kryształach. Ponieważ nie uwzględniamy warunków jakie spełniają wektory pola elektromagnetycznego na granicach ośrodków (próżnia jest także traktowana jako ośrodek), nasze rozważania dotyczą przestrzeni wypełnionej ośrodkiem krystalicznym, a w rzeczywistości propagację fal w makroskopowych próbkach krystalicznych.

Można badać właściwości rozwiązań równania (3.12b) w sposób, który nie zależy od wyboru układu współrzędnych (por. [1]), jednak rozważania są znacznie prostsze jeżeli oś z ortogonalnego układu współrzędnych skierować wzdłuż wektora propagacji fali
[2,3]. Wtedy osie x i y leżą w płaszczyźnie stałej fazy π. Z równania (3.10c) wynika, że dla tak wybranego układu współrzędnych D_z = 0.

W wybranym przez nas układzie współrzędnych ze wszystkich elementów symetrycznej macierzy reprezentującej tensor
istotne są trzy elementy
. Te elementy zależą od wyboru układu współrzędnych, a w szczególności od wektora
. W wybranym układzie współrzędnych układ równań liniowych (3.12b) przyjmuje postać

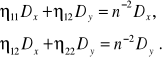
(3.14a,b)

Aby układ równań jednorodnych (3.14) miał rozwiązanie jego wyznacznik

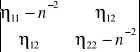
musi znikać. Ten warunek prowadzi do równania dwukwadratowego. Podajmy jego rozwiązania

. (3.15a)

Jak widać w ogólnym przypadku, tj. dla wektora propagacji
dowolnie skierowanego względem kierunków symetrii kryształu, w krysztale rozchodzą się dwie fale o prędkościach

(3.15b)

Wprowadzimy wektory falowe odpowiadające dwóm falom o prędkościach fazowych
. Zgodnie z definicją (1.7c) wektora k

. (3.15c)

Jak widać
, a więc obydwie fale poruszają w tym samym kierunku
. Określimy polaryzację każdej z tych fal. W tym celu kolejno podstawimy rozwiązania (3.15a) do układu równań (3.14), otrzymamy

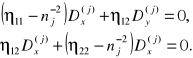
(3.16a,b)

Gdy
to wektory
są do siebie prostopadłe. Natomiast gdy

zawsze można znaleźć takie kombinacje liniowe rozwiązań, które są do siebie prostopadłe. Na ogół odpowiadają one falom spolaryzowanym kołowo albo eliptycznie.

Gdy
oraz
to ze wzoru (16a) wnioskujemy, że składowe wektora indukcji są proporcjonalne

.

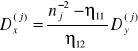
Jak widać gdy wartości własne różnią się (
) mamy do czynienia z wektorami spełniającymi związek

. Zatem gdy wartości własne
nie są zwyrodniałe to wektory indukcji spełniają kryterium polaryzacji liniowej, a więc krysztale rozchodzą się dwie fale liniowo spolaryzowane w kierunkach prostopadłych do siebie (rys. 3.2). Współczynnik załamania jednej z nich n_o nie zależy od kierunku propagacji fali, a drugiej n_e - zależy.

Własności pierwszej fali są typowe dla ośrodków izotropowych, np. szkieł. Do czasu odkrycia dwójłomności badano tylko własności szkieł, które są optycznymi ośrodkami izotropowymi, charakteryzowanym przez jeden współczynnik
, który jest niezależny od kierunku propagacji fali. Współczynnik
nazywa się zwyczajnym (francuskie ordinary). Fala o współczynniku załamania n_e może się rozchodzić tylko w ośrodkach anizotropowych, dlatego nazwano ją i odpowiedni współczynnik załamania nazwano nadzwyczajnymi (francuskie ekstraordinary). Powyższe oznaczenia mają jedynie sens historyczny. Ośrodki optyczne o tych własnościach nazywamy dwójłomnymi. Dodajmy, że izotropowe przezroczyste ośrodki dielektryczne mogą wykazywać własność dwójłomności pod wpływem jednoosiowych deformacji i pola elektrycznego. Niektóre ciecze stają się aktywne optycznie pod wpływem pola magnety­cznego. Także niektóre płynące ciecze także są takimi ośrodkami.

3.2 Ośrodki izotropowe i jednoosiowe

Dla szkieł, a także dla kryształów należących do krystalograficznego układu regularnego tensor stałych dielektrycznych ma postać

.

Łatwo sprawdzić, że dla tych ośrodków tensor
ma także bardzo prostą postać

Jak widać w ośrodkach optycznie izotropowych (np. w rubinie i szkłach) rozchodzą się w nich tylko fale o współczynniku załamania n_o.

W przypadku kryształów należących do układów tetragonalnych, trygonalnych i heksagonalnych dwie z wartości własnych tensora przenikalności dielektrycznej są jednakowe. Niech
będzie kierunkiem osi symetrii kryształów należących do wymienionych trzech układów (tj. osią czterokrotną, trójkrotną albo sześciokrotną), tensor
ma następującą postać [1]

. (3.20a)

Można sprawdzić, że gdy
ma postać [1]

, (3.20b)

to
, tzn.
(3.20b) jest tensorem przenikalności odpowiadającym tensorowi (3.20a).

Oś
nazywa się osią optyczną kryształu albo binormalną (por. [2]). Wektory
i
określają płaszczyznę zwaną płaszczyzną główną (rys. 3.2).

Rys. 3.2 Płaszczyzna główna

Wektorem własnym tensora (3.20b) jest
, odpowiada mu wartość własna
. Wyni­ka to z relacji

. (3.20c)

Każdy wektor
leżący w płaszczyźnie prostopadłej do wektora
(
) jest wektorem własnym tensora
odpowiadającym wartości własnej
. Kryształy, dla których tensor przenikalności dielektrycznej i stałych dielektrycznych mają postać (3.20) nazywa się jednoosiowym.

Dla kryształów jednoosiowych równanie (3.12b) ma postać

, (3.21)

gdzie
. Równanie (3.21) jest ma postać zagadnienia na wartości własne: macierz

działa na wektor D, który odpowiada znikającej wartości własnej macierzy U. Mamy określić współczynnik załamania n i wektor D. Rozpatrzymy wnioski, które wynikają z równania (3.21).

I. Załóżmy, że propagacja fali odbywa się w kierunku osi optycznej, tj.
. Wtedy nie można określić płaszczyzny głównej. Dla tak wybranego kierunku propagacji fali składowa D równoległa do
znika, tj.
, a więc
. To oznacza, że wyrazy (3.21) proporcjonalne do diad nie dają wkładu, zatem równanie (3.21) przyjmuje postać

. (3.22)

Gdy
to
. Jak widzimy każdy wektor indukcji prostopadły do osi optycznej jest rozwiązaniem równania (3.12b). Także każda kombinacja liniowa
dowolnych dwóch wektorów indukcji
prostopadłych do osi optycznej jest rozwiązaniem odpowiadającym współczynnikowi n_o. Gdy obydwa współczynniki α β są rzeczywiste albo urojone to D odpowiada fali liniowo spolaryzowanej. Natomiast gdy współczynniki te są liczbami zespolonymi to D może określać falę kołowo albo eliptycznie spolaryzowaną. Wszystkim tym falom odpowiada ten sam współczynnik załamania n_o.

II. Niech fala będzie spolaryzowana prostopadle do płaszczyzny głównej, tj.

.

Ponieważ
, wyrazy (3.21) proporcjonalne do diad nie dają wkładu, a stąd wynika, że n = n_o. Jak widać fala zwyczajna charakteryzowana przez nieznikający wektor indukcji D_o jest spolaryzowana prostopadle do płaszczyzny głównej.

III. Gdy wektor indukcji jest równoległy do wektora
to odpowiada mu współczynnik załamania zależny od kąta jaki tworzą wektory
i
. Wektor
jest prostopadły do wektora
. To oznacza, że wektor indukcji
spełnia warunek prostopadłości do kierunku propagacji fali:
. (Rys. 3.3)

Po podstawieniu wektora D_e do równania (3.21) otrzymamy równanie

, (3.23)

z którego wynika, że
gdy

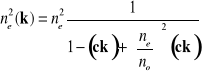
. (3.24)

Ponieważ współczynnik załamania fali spolaryzowana liniowo w płaszczyźnie głównej zależy od kierunku propagacji jest to fala nadzwyczajna. Ponieważ wektor
określa oś, która nie ma określonego zwrotu można przyjąć, że
. Zatem kwadrat współczynnika
jest wielkością dodatnią dla wszystkich orientacji osi optycznej względem wektora propagacji fali. Współczynnik załamania
zawarty jest między
dla
i
gdy
.

W przypadku kryształów należących do pozostałych układów krystalograficznych mamy do czynienia z trzema różnymi wartościami własnymi (
) i dwoma osiami optycznymi
i
. Tensor
ma postać [1]

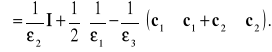
(3.25)

W kierunkach
i
mogą się rozchodzić fale dowolnie spolaryzowane [1].

Podkreślimy zasadniczą różnicę istniejącą pomiędzy własnościami optycznymi ośrod­ków izotropowych i anizotropowych. W przypadku tych pierwszych w każdym kierunku mogą się rozchodzić dowolnie spolaryzowane fale. W ośrodkach optycznie anizotropowych jest możliwe tylko gdy fale rozchodzą się w kierunkach osi optycznych. Dla innych kierunków propagacji mogą jedynie rozchodzić się fale liniowo spolaryzowane. Jak widać próbki przezroczystych kryształów dielektrycznych pozwalają wpływać na stan polaryzacji światła.

3.3 Promienie

W większości doświadczeń nie badamy propagacji powierzchni stałej fazy, lecz transport energii. Kierunek transportu energii określa wektor strumienia energii s

, (3.26)

Będziemy go nazywali promieniem. Na podstawie rys. 3.1 wnioskujemy, że wektor s leży w płaszczyźnie określonej przez wektory
, lecz nie jest równoległy do
. Wektor
nazywany jest wektorem kierunku promienia. Jeśli na drodze fali świetlnej ustawić nieprzezroczysty ekran z dostatecznie wąską szczeliną to wektor
określa kierunek sposób promienia wydzielonego w ten sposób (rys. 3.4) [3].

Rys. 3.4

Prędkość transportu energii u nazywamy prędkością grupową. Jest ona związana z prędkością fazową światła v w ośrodku i kątem
jaki tworzą wektory
i

. (3.27)

Wprowadzimy q - współczynnik załamania promienia

. (3.28)

Zwiążemy go z n - współczynnikiem załamania fali. W tym celu rozpatrzymy iloczyn nq

. (3.29)

Ze wzoru (3.26) wynika, że

. (3.30a,b)

Zbadamy iloczyny wektorowe
i
. Wykorzystamy związki (3.10) i (3.20)

, (3.31a)

. (3.31b)

Równania (3.31) można zapisać w postaci podobnej do równań Maxwella (3.10)

. (3.32a-c)

Dla przezroczystych kryształów niemagnetycznych zamiast układu równań (3.10) dla fal elektromagnetycznych można używać układu równań (3.32) dla promieni. Opis propagacji promieni w ośrodkach anizotropowych można zbudować w podobny sposób jak opis propagacji fal. Zauważymy, że zazwyczaj doświadczenia optyczne przeprowadzane są dla promieni, nie fal.

Literatura:

[1] F.I. Fedorow, Optika anizotropnych sred, Izdatielstwo Akademii Nauk BSSR, Minsk, 1958, R. III.

[2] F. Ratajczyk, Optyka ośrodków anizotropowych, PWN, Warszawa, 1994

[3] Ju. I. Sirotin, M.P. Szaskolskaja, Osnowy kristałłofizyki, Nauka, Moskwa, 1979, R. IV.

1

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---