STATYSTYKA - konspekt wykładów 2 i 3

Miary statystyczne

Statystyki próby - parametry statystyczne liczone w oparciu o zbiorowość próbną

1. Miary tendencji centralnej (inaczej: położenia) - wśród nich miary średnie (przeciętne). (skupienie wartości wokół której skupiają się wszystkie pozostałe)

2. Miary zmienności (inaczej: rozrzutu, rozproszenia, dyspersji). (siła zróżnicowania wartości badanej cechy)

3. Miary asymetrii (inaczej: skośności), (kierunek zróżnicowania wartości cechy i stopnia asymetrii)

4. Miary koncentracji (kurtozy)

• Miary klasyczne

• Miary pozycyjne

Wyznaczanie z danych indywidualnych

Miary średnie

Średnia arytmetyczna

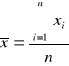
(nieważona)

Interpretacja

Wartość przedstawiająca środek układu.

Średnia geometryczna

,

Średnia harmoniczna

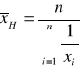
Mediana

A. nieparzysta liczba obserwacji

B. parzysta liczba obserwacji

Interpretacja

Liczba w połowie szeregu

Równanie Pearsona:

Kwantyle

• kwartyle (dzielą zbiorowośc na 4 liczebnie równe części)

• decyle (na 10 części)

• percentyle (centyle) (na 100)

• kwartyl pierwszy ( dolny - Q₁) - punkt na skali pomiarowej, poniżej którego znajduje się 25 % wyników;

• kwartyl drugi ( mediana - Q₂ ) - punkt na skali pomiarowej, poniżej którego znajduje się 50 % wyników;

• kwartyl trzeci ( górny - Q₃ ) - punkt na skali pomiarowej, poniżej którego znajduje się 75 % wyników.

Miary zróżnicowania

Rozstęp (Różnica pomiędzy największą i najmniejszą wartością zmiennej)

Rozstęp międzykwartylowy

Odchylenie ćwiartkowe (jak kwartale odchylają się przeciętnie od mediany)

Typowy obszar zmienności (pozycyjny)

Wariancja (Jest ona średnią kwadratu odchyleń wartości zmiennej od wartości średniej. Znana jest także jako drugi moment centralny (m₂ ). Zawiera informacje o średnim odchyleniu zmiennej od wartości średniej.)

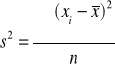
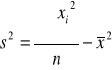
Odchylenie standardowe (Dodatnia wartość pierwiastka kwadratowego z wariancji. Jest miarą średniego odchylenia wyników pomiaru od wartości średniej)

Typowy obszar zmienności (klasyczny)

.

Współczynniki zmienności

Klasyczny współczynnik zmienności:

Pozycyjny współczynnik zmienności:

• 0 - 20% - zróżnicowanie cechy słabe,

• 20 - 40% - umiarkowane,

• 40 - 60% - silne,

• 60% i więcej - bardzo silne.

Miary asymetrii

• asymetria prawostronna (dodatnia)

• asymetria lewostronna (ujemna)

Współczynnik asymetrii Pearsona

Pozycyjny współczynnik asymetrii

Klasyczny współczynnik asymetrii

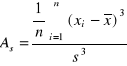
moment centralny trzeciego rzędu

Wyznaczanie z danych pogrupowanych

Średnia arytmetyczna

1. W szeregu punktowym

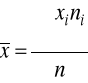
(średnia arytmetyczna ważona)

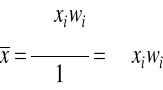
lub:

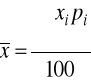
2. W szeregu przedziałowym

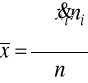
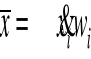
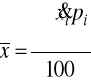
3. Średnia ważona jako tzw. „średnia ze średnich”

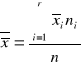
4. Średnia dla wskaźników natężenia

- gdy cechy są wielkościami stosunkowymi, np. gęstośc zaludnienia, plon, ceny, wskaźniki ekonomiczne.

Dominanta

1. W szeregu punktowym

2. W szeregu przedziałowym

wzór interpolacyjny:

Uwaga

Zamiast liczebności - częstości.

Mediana

1. W szeregu punktowym

2. W szeregu przedziałowym

Wzór interpolacyjny:

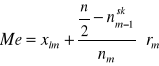
Kwartyle

1. W szeregu punktowym

2. W szeregu przedziałowym

Wzory interpolacyjne

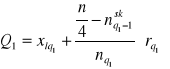
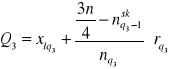
Wariancja i odchylenie standardowe

1. W szeregu punktowym

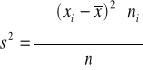
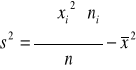
Uwaga.

Z rozkładu częstości:

2. W szeregu przedziałowym

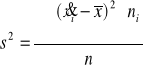
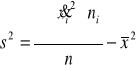
Uwaga.

Z rozkładu częstości

Klasyczny współczynnik asymetrii

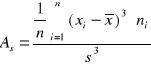
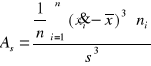
Analiza korelacji (czy jest zalezność, jej siła, kierunek, kształt)

Analiza regresji:

- szereg korelacyjny

- diagram korelacyjny

Kierunek:

-dodatnia (obie wartości rosną)

-ujemna (jedna rośnie, druga maleje)

Kształt:

-liniowa

-krzywoliniowa

X - zmienna niezależna (objaśniająca)

Y - zmienna zależna (objaśniana).

Y = f(X)

Miary korelacji

Współczynnik korelacji liniowej r Pearsona (do pomiaru cech mierzalnych)

- obliczanie i interpretacja

1) dla szeregu szczegółowego

=
,

=
,

,

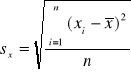
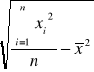
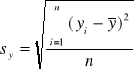
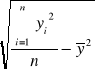
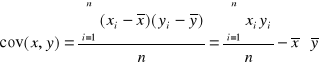
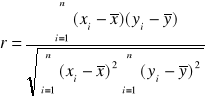
2) dla danych pogrupowanych (tablica korelacyjna)

.

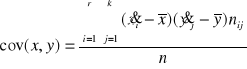
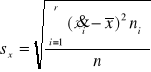
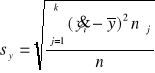
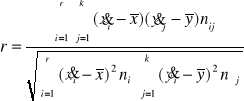
Analiza regresji

Równanie r. - ilościowy wyraz zależności między wartościami zmiennej X i odpowiadającymi im wartościami zmiennej zależnej Y.

Y = f(X) + czynnik losowy - regresja prosta

Y = f(X₁, X₂, X₃,…) + czynnik losowy - regresja wieloraka

Metoda najmniejszych kwadratów (MNK)

Współczynnik determinacji (ocena dobroci dopasowania linii regresji do danych empirycznych) R²

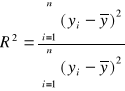
wyrażony w %; miara stopnia w jakim model wyjaśnia kształtowanie się zmiennej Y; jaka część zmienności cechy Y została w yjasniona wpływem zmienności cechy X, tj. wyjaśniona przez znalezione równanie regresji.

Współczynnik korelacji rang Spearmana (do oceny kierunku i siły korelacji; cechy mierzalne - ale liczba wariantów przyjmowanych przez te cechy jest niewielka; cechy niemierzalne - wyrażone w skali porządkowej)

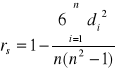
Miary współzależności cech jakościowych (współczynniki kontyngencji)

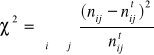
Współczynnik Yule'a

.

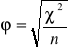
Współczynnik Czuprowa T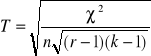
,

Współczynnik V Cramera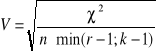

Przypadek cech dychotomicznych

- przy założeniu że wszystkie liczebności

lub stosując poprawkę Yates'a:

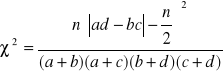
- gdy którakolwiek z liczebności

Współczynnik Kendalla Q:

.

13