1 Wstęp teoretyczny

Każdy przewodnik metaliczny składa się z atomów w których elektrony zewnętrznej powłoki nie są mocno związane z atomem i mogą swobodnie poruszać się wewnątrz metalu w przestrzeni między atomami. Elektrony te jednak nie mogą opuścić wnętrza metalu, z powodu istnienia sił wywieranych na elektrony zbliżające się do powierzchni metalu,

Aby elektron mógł opuścić metal należy mu dostarczyć energii L_W = e*U zwanej pracą wyjścia. praca wyjścia ma stałą wartość dla danego metalu.

Zjawisko fotoelektryczne opisuje kwantowy charakter światła, jest to wzajemne oddziaływanie na siebie promieniowania i materii. Charakteryzuje się absorbcją fotonów przez materię i związane z nią pobudzenie atomów lub uwolnienie elektronów. Zjawisko fotoelektryczne zewnętrzne (fotoemisja) występuje, gdy elektron opuszcza powierzchnię ciała. Emisję elektronu mogą spowodować tylko te fotony, których energia jest równa pracy wyjścia lub jest większa od niej.

h*γ = L_W

Nadmiar energii kwantu zostanie przekazany fotoelektronowi w postaci energii kinetycznej, co przedstawia wzór Einsteina - Millikana

Jeżeli lampę elektronową diodę lub fotokomórkę włączy się w obwód, to nawet przy braku napięcia między elektrodami w obwodzie popłynie prąd elektryczny. Wskazuje to ,że elektrony są emitowane z powierzchni metalu z pewną prędkości i mogą kosztem swojej energii kinetycznej przebyć drogę między katodą i anodą. gdy między katodą i anodą istnieje pole hamujące elektrony (minus na anodzie), to do anody dotrą tylko te, których energia kinetyczna jest większa od pracy pola hamującego.

gdzie:

m - masa elektronu

e - ładunek elektronu

V_X - składowa prędkości elektronu w kierunku pola

U_H - napięcie hamujące

2 Ćwiczenie

Wyznaczanie prędkości wyjścia elektronów i stałej Plancka metodą pola hamującego

Przy zmianie długości fal promieniowania elektromagnetycznego odczytywano wartość napięcia hamującego z miernika cyfrowego.

Zestawienie wyników

λ	1/λ	U
[nm]	[1/nm]*10^-3	[V]
380	0,002632	1,211
385	0,002597	1,172
390	0,002564	1,130
395	0,002532	1,101
400	0,0025	1,141
405	0,002469	1,105
410	0,002439	1,062
415	0,00241	1,026
420	0,002381	0,987
425	0,002353	0,924
430	0,002326	0,919
435	0,002299	0,892
440	0,002273	0,862
445	0,002247	0,828
450	0,002222	0,796
455	0,002198	0,775
460	0,002174	0,752
465	0,002151	0,736
470	0,002128	0,711
475	0,002105	0,695
480	0,002083	0,677
485	0,002062	0,665

Z wyników możemy wnioskować że zwiększając częstotliwość fali, zwiększa się wartość napięcia hamującego dla którego przez obwód nie popłynie prąd.

Obliczenia

Wyznaczenie stałej Plancka

y = ax + b

a = 1121,5

b = -1,681

R² = 0,9909

hc/e=1121,5

Obliczenie pracy wyjścia

W= h*c/λ

W= 6,656*10^-34 *
/ 430 [J*s/s=J]

W = 7,2267*10¹⁹ [J]

Rachunek błędu

- określenie błędu procentowego stałej Plancka w porównaniu z wartością tablicową

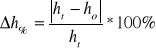
h_t - wartość stałej z tablic ( 6,625*10^-34)

h_o - wartość stałej obliczona

4 Wnioski i spostrzeżenia.

Wraz ze wzrostem długości fali λ, wzrasta prędkość elektronu w polu elektrycznym. Obliczona w ćwiczeniu stała Plancka różniła się od rzeczywistej podawanej w tabelach o 1,79 %. Błędy wynikać mogą z powodu niesprawnych urządzeń pomiarowych lub czynnika ludzkiego.

---