Wydział: Geodezja i Kartografia |
Dzień/godz.: Czwartek 17:15 |
Data: 29.03.2007r.
|
Nr zespołu: 2 |
Nazwisko i Imię |
Ocena z przygotowania: |
Ocena ze sprawozdania: |
Ocena: |
1. Pruś Remigiusz |
5 5 5 |
|
|
2. Radzyński Artur |
|
|
|
3. Sulej Paweł |
|
|
|
Prowadzący: mgr inż. Aleksandra Czapla |
Podpis prowadzącego: |
|
|
ĆWICZENIE 19
Wyznaczenie współczynnika lepkości.
Cel ćwiczenia.
Celem ćwiczenia jest wyznaczenie współczynnika lepkości badanych cieczy, którymi były gliceryna i olej silnikowy.
Podstawy fizyczne.
Lepkością cieczy nazywamy siłę tarcia pomiędzy warstwami cieczy. Siła ta powstaje podczas ruchu jednej warstwy cieczy wzdłuż drugiej. Poruszająca się warstwa cząsteczek cieczy nadaje warstwom cieczy znajdującym się w różnej odległości od niej różnych prędkości.
W wyniku ruchów warstw cieczy wywołanych poruszającym się w niej ciałem, powstała siła lepkości działająca na ciało jest proporcjonalna do gradientu prędkości przesuwanych warstw cieczy i powierzchni ciała. Wyraża to wzór:
![]()
(1)
gdzie
η - współczynnik lepkości
Vx - prędkość warstwy cieczy
Z - odległość warstwy od punktu 0 na osi Z
S - powierzchnia poruszającego się ciała
Przepływ cieczy wokół dowolnego ciała zależy od gęstości cieczy ρ i współczynnika lepkości cieczy η, charakterystycznego wymiaru liniowego l i od prędkości przepływu v. Charakter przepływu zależy od bezwymiarowej kombinacji tych wielkości i zwany jest liczbą Reynoldsa ( jest to liczba nie mianowana):
![]()
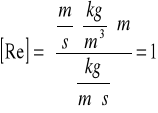
(2)
W przypadku liczb Reynoldsa, Re<<1 najistotniejszym składnikiem siły oporu jest lepkość, a przepływ cieczy nazywamy laminarnym.
Dla przepływu laminarnego Stokes wprowadził wzór na siłę oporu działającą na kulkę opadającą pod wpływem siły ciężkości w cieczy wypełniającej całą przestrzeń:
![]()
oraz ![]()
(3)
gdzie
V - prędkość kulki
r - promień kulki
η - współczynnik lepkości
Mając na uwadze ruch kulki w cieczy wypełniającej cylinder o promieniu R, wzdłuż jego osi, należy wprowadzić poprawkę do współczynnika K. Poprawka ta uwzględnia wpływ obecności ścianek naczynia na ruch kulki. Wówczas współczynnik K przyjmie postać:
![]()
(4)
Ruch kulki po pewnym czasie ustala się i można przyjąć, że jest on ruchem jednostajnym z prędkością ![]()
. Ciało będzie się poruszało z ![]()
wówczas, gdy siły działające na nie zrównoważą się. Prędkość graniczna wyrażana jest wzorem:
![]()
(5)
Wyznaczenie współczynnika lepkości dokonaliśmy w oparciu o wzór:
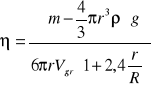
(6)
gdzie:
ρ - ciężar właściwy badanej cieczy
R - średnice wewnętrzne rur z cieczami
m - masa wykorzystywanych kulek
r - średnica wykorzystywanych kulek
g - przyspieszenie ziemskie
Otrzymane wyniki i ich opracowanie.
W przeprowadzonym ćwiczeniu badaliśmy lepkość cieczy, w której opadała metalowa kulka pod wpływem siły ciężkości. Ciecze znajdowały się w rurach, których średnice wewnętrzne wynosiły dla gliceryny ![]()
a dla oleju![]()
. Ciężar właściwy badanych substancji odczytaliśmy z tablic i wynosi on dla gliceryny ![]()
i dla oleju silnikowego ![]()
. Czas mierzyliśmy stoperem, którego błąd pomiaru oszacowaliśmy na ![]()
,drogę odczytywaliśmy przy użyciu taśmy pomiarowej umieszczonej wzdłuż cylindra z ![]()
. Zestaw metalowych kulek, który otrzymaliśmy składał się z 5 kulek małych, 5 średnich i 3 dużych. Ich średnice wyznaczyliśmy używając śruby mikrometrycznej z błędem ![]()
a masę używając wagi laboratoryjnej z błędem ![]()
. Błąd miejsca zera wagi wynosił: + 2,6 mg.
Wyniki pomiarów średnicy kulek i ich masy.
Masa kulek została wyznaczona jako średnia arytmetyczna z wyników ważenia wszystkich kulek tego samego rodzaju. Natomiast średnica każdej kulki była mierzona dla każdej osobno. Wyniki zawiera poniższa tabela:
Ilość |
Rodzaj kulek |
Masa [kg] |
r [mm] |
Średnica [mm] |
3 |
Duże |
0.0001746 |
1,73 |
3,46 |
|
|
|
1,74 |
3,47 |
|
|
|
1,73 |
3,46 |
5
|
Średnie
|
0.0001097 |
1,48 |
2,96 |
|
|
|
1,49 |
2,97 |
|
|
|
1,49 |
2,97 |
|
|
|
1,49 |
2,97 |
|
|
|
1,48 |
2,96 |
5 |
Małe
|
0.0000637 |
1,23 |
2,46 |
|
|
|
1,23 |
2,45 |
|
|
|
1,24 |
2,47 |
|
|
|
1,23 |
2,46 |
|
|
|
1,23 |
2,46 |
Tab.1. Pomiary średnicy i masy kulek.
Wyznaczenie prędkości granicznej.
Kolejnym etapem ćwiczenia było wyznaczenie prędkości granicznej, z jaką poruszały się kulki w badanych cieczach. W tym celu mierzyliśmy czas, w którym kulka pokonywała drogę S. Odcinek S uznajemy za drogę, którą opadająca kulka pokonuje ruchem jednostajnym z prędkością ![]()
. Prędkość graniczną obliczyliśmy z wzoru:
![]()
(7)
Zatem błąd tak obliczonej prędkości granicznej wynosi metodą różniczki zupełnej wynosi:
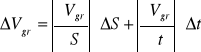
(8)
Wyniki pomiarów i obliczeń dla gliceryny:
GLICERYNA |
||||||
Rodzaj kulek |
t [s] |
Δt [s] |
S[m] |
ΔS[m] |
Vgr[m/s] |
ΔVgr[m/s] |
Małe
|
10,38 |
0,21 |
0,507 |
0,001 |
0,049 |
0,00104 |
|
10,34 |
0,21 |
0,507 |
0,001 |
0,049 |
0,00105 |
|
10,41 |
0,21 |
0,507 |
0,001 |
0,049 |
0,00103 |
Średnie
|
9,84 |
0,21 |
0,373 |
0,001 |
0,038 |
0,00087 |
|
9,79 |
0,21 |
0,373 |
0,001 |
0,038 |
0,00088 |
|
9,81 |
0,21 |
0,373 |
0,001 |
0,038 |
0,00088 |
|
9,70 |
0,21 |
0,373 |
0,001 |
0,038 |
0,00090 |
|
9,72 |
0,21 |
0,373 |
0,001 |
0,038 |
0,00089 |
Duże
|
12,16 |
0,21 |
0,356 |
0,001 |
0,029 |
0,00056 |
|
12,12 |
0,21 |
0,356 |
0,001 |
0,029 |
0,00057 |
|
12,28 |
0,21 |
0,356 |
0,001 |
0,029 |
0,00055 |
|
12,31 |
0,21 |
0,356 |
0,001 |
0,029 |
0,00055 |
|
12,22 |
0,21 |
0,356 |
0,001 |
0,029 |
0,00056 |
Tab.2.Obliczenie Vgr dla gliceryny.
Tabela z wynikami obserwacji i obliczeniami dla oleju silnikowego:
OLEJ SILNIKOWY |
||||||
Rodzaj kulek |
t [s] |
Δt [s] |
S[m] |
ΔS[m] |
Vgr[m/s] |
ΔVgr[m/s] |
Małe
|
3,47 |
0,21 |
0,575 |
0,001 |
0,166 |
0,0098 |
|
3,53 |
0,21 |
0,575 |
0,001 |
0,163 |
0,0095 |
|
3,62 |
0,21 |
0,575 |
0,001 |
0,159 |
0,0091 |
Średnie
|
3,13 |
0,21 |
0,4 |
0,001 |
0,128 |
0,0085 |
|
3,25 |
0,21 |
0,4 |
0,001 |
0,123 |
0,0079 |
|
3,15 |
0,21 |
0,4 |
0,001 |
0,127 |
0,0084 |
|
3,21 |
0,21 |
0,4 |
0,001 |
0,125 |
0,0081 |
|
3,19 |
0,21 |
0,4 |
0,001 |
0,125 |
0,0082 |
Duże
|
3,9 |
0,21 |
0,366 |
0,001 |
0,094 |
0,0051 |
|
3,88 |
0,21 |
0,366 |
0,001 |
0,094 |
0,0051 |
|
3,88 |
0,21 |
0,366 |
0,001 |
0,094 |
0,0051 |
|
3,85 |
0,21 |
0,366 |
0,001 |
0,095 |
0,0052 |
|
3,91 |
0,21 |
0,366 |
0,001 |
0,094 |
0,0050 |
Tab.3. Obliczenie Vgr dla oleju silnikowego.
Znając prędkość graniczną jesteśmy już w stanie obliczyć współczynniki lepkości badanych cieczy zgodnie z wzorem (6). Korzystając z metody różniczki zupełnej obliczyliśmy także błąd wyznaczanych współczynników lepkości, który jest równy:
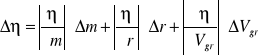
(9)
gdzie poszczególne człony wynoszą :
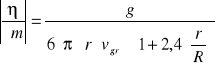
(10)
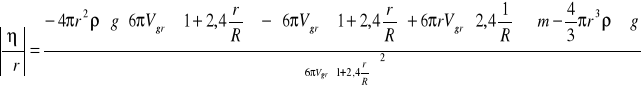
(11)
Błąd prędkości granicznej został już wyznaczony wcześniej. Tabela 3 przedstawia obliczone lepkości badanych cieczy wraz z ich błędami:
|
GLICERYNA |
OLEJ SILNIKOWY |
||
Rodzaj kulek
|
|
|
|
|
Duże
|
0,7647883 |
0,0697883 |
0,2464279 |
0,0303562 |
|
0,7578826 |
0,0694262 |
0,2496112 |
0,0304961 |
|
0,7669987 |
0,0696327 |
0,2570804 |
0,0312295 |
Średnie
|
0,7379613 |
0,0991316 |
0,2391711 |
0,0402997 |
|
0,7298012 |
0,0985062 |
0,2471081 |
0,0410483 |
|
0,7312921 |
0,0985062 |
0,2395048 |
0,0402117 |
|
0,7230921 |
0,0988891 |
0,2440668 |
0,0405302 |
|
0,7289618 |
0,0995191 |
0,2437559 |
0,0410697 |
Małe
|
0,6827413 |
0,145454 |
0,2324062 |
0,0533752 |
|
0,6853635 |
0,145691 |
0,2325825 |
0,0533752 |
|
0,6845731 |
0,143863 |
0,2298549 |
0,0528672 |
|
0,6911632 |
0,145216 |
0,2294266 |
0,0529238 |
|
0,6861101 |
0,145454 |
0,2330021 |
0,0531284 |
Tab.3.Współczyniki lepkości badanych cieczy oraz ich błędy.
Wyznaczenie ostatecznej wartości współczynnika lepkości.
Nasze obserwacje należy traktować jako pomiary o niejednakowej dokładności, ponieważ współczynnik lepkości wyznaczaliśmy za pomocą różnych kulek i innej liczbie kulek danego rodzaju. Ostateczną wartość lepkości oleju silnikowego i gliceryny oraz jej błędu dokonujemy w oparciu o wzory na średnią ważoną, która jest zdefiniowana następująco:
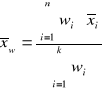
(12)
Wagę ![]()
definiujemy jako odwrotność kwadratu niepewności otrzymanych wyników bądź obserwacji. Niepewność systematyczna tak obliczonej średniej ważonej przybiera wówczas postać:
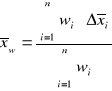
(13)
W oparciu o wzory (12)-(13) otrzymaliśmy następujące wartości lepkości i jej błędu dla poszczególnych rodzajów kulek:
|
GLICERYNA |
OLEJ SILNIKOWY |
||||
Rodzaj kulki |
|
|
|
|
|
|
Duże
|
205,3217 |
0,250930842
|
0,03068449
|
1085,189 |
0,76321028
|
0,069615101
|
|
207,469 |
|
|
1075,255 |
|
|
|
206,2403 |
|
|
1025,345 |
|
|
Średnie
|
101,7597 |
0,242675327
|
0,040625416
|
615,7386 |
0,730218348
|
0,098907427
|
|
103,0559 |
|
|
593,4849 |
|
|
|
103,0559 |
|
|
618,4365 |
|
|
|
102,2594 |
|
|
608,755 |
|
|
|
100,9688 |
|
|
592,8665 |
|
|
Małe |
47,26598 |
0,231444317
|
0,053132215
|
351,0112 |
0,685987746
|
0,145129657
|
|
47,11233 |
|
|
351,0112 |
|
|
|
48,3172 |
|
|
357,7893 |
|
|
|
47,42104 |
|
|
357,0245 |
|
|
|
47,26598 |
|
|
354,2799 |
|
|
Tab.4. Lepkość badanych cieczy i jej błędy w zależności od rodzaju kulki.
Stosując wzory (12)-(13) ponownie do wartości z Tab.4. otrzymujemy ostateczne wartości i błędy szukanych współczynników lepkości:
GLICERYNA:
![]()
OLEJ SILNIKOWY:
![]()
Wnioski
Na podstawie otrzymanych wyników naszych obliczeń widać, że badane ciecze mają inne współczynniki lepkości. Ma to oczywiście wpływ na ruch ciał w badanych cieczach. Prędkość graniczna w olej silnikowym jest kilka razy wyższa niż w glicerynie. Również ciężar właściwy cieczy ma znaczenie na opory ruchu w niej zgodnie z zasadą, że im ciecz ma większy ciężar właściwy tym ciało poruszające się w niej napotyka na większe opory. Uważamy, że największy wpływ na ostateczną wartość błędu współczynnika lepkości miał pomiar czasu. O ile dokładność stopera określamy na poziomie 0,01 s to precyzyjne określanie przez osobę mierzącą momentu startu i stopu pomiaru czasu było bardzo trudne i obarczone dużym błędem.
3
Wyszukiwarka