1.3. JEDNOSTKI MIAR
Pomiar jest to porównywanie danej wielkości z przyjętą jednostką miary. Przy pomiarach geodezyjnych najczęściej określa sie elementy długościowe i kątowe oraz oblicza się w oparciu o nie inne elementy, na przykład współrzędne punktu w przyjętym układzie odniesienia, azymuty wskazanych kierunków itp. Stąd konieczne jest ustalenie jednostek miar długości i kąta. Jednostki te potocznie nazywa się miarami.
Do oznaczania długości w Polsce przyjęto system metryczny. Miarą jednostkową w tym systemie jest metr (oznaczany małą literą m), którego wielokrotności i podwielokrotności są ułożone w systemie dziesiętnym (km, hm, dcm, cm i mm).
Miara kąta płaskiego może być określona w dwojaki sposób.
W pierwszym sposobie jednostką główną jest kąt pełny, tj. kąt środkowy, któremu odpowiada łuk okręgu koła o długości równej jego obwodowi.
Drugi sposób określania kąta płaskiego opiera się na utworzeniu stosunku łuku (ł) koła, odpowiadającego danemu kątowi jako środkowemu, i długości promienia (r).
1.3.1. Miary kątowe
W zależności od sposobu podziału kąta rozróżniamy miarę stopniową, gradową, tysięczną, czasowo-kątową i łukową.
A. Miara stopniowa
Miara stopniowa kąta powstaje przez podział kąta pełnego na 360 części, zwanych stopniami. Podział ten jest dawnego pochodzenia (około 4 000 - 5 000 lat p.n.e.) i dlatego, zgodnie ze stosowanym wówczas w Babilonii sześćdziesiątkowym systemem liczenia, podział wtórny odbywa się według tego systemu. W ten sposód mamy:
![]()
kąta pełnego;
1 = 60 i 1 = 60.
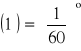
oraz 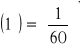
Jako podwielokrotności stopnia mogą być używane dziesiętne części stopnia. System ten nazywany bywa w literaturze systemem mieszanym. Stopień dzieli się tu na 100 minut, a minuta na 100 sekund.
Chcąc przejść z systemu sześćdziesiątkowego na tzw. stopniowo-dziesiętny zachowujemy wartości stopni bez zmian, natomiast minuty i sekundy kątowe przemnażamy przez poniższe zamienniki:
![]()
![]()
Miara stopniowa kąta jest rozpowszechniona niemal we wszystkich gałęziach nauk matematyczno-fizycznych i technice.
B. Miara gradowa
Miara gradowa polega na podziale kąta pełnego na 400 części i stosowaniu, przy dalszym podziale, systemu dziesiętnego. W ten sposób mamy:
![]()
kąta pełnego;
![]()
i ![]()
.
Z powodu wielu cech dodatnich, miara gradowa zdobyła sobie szerokie uznanie w geodezji.
C. Miara tysięczna
Tysięczna jest jedną sześciotysięczną częścią kąta pełnego.
Zapisuje się ją w następujący sposób:
![]()
Jest podstawową miarą stosowaną w artylerii.
D. Miara czasowo-kątowa
Miara czasowo-kątowa powstaje przez podział kąta pełnego w sposób analogiczny do podziału doby na godziny, minuty i sekundy. Mamy więc:
![]()
kąta pełnego;
![]()
i ![]()
Miara czasowo-kątowa znajduje zastosowanie prawie wyłącznie w niektórych zagadnieniach astronomii.
E. Miara łukowa
Dla łukowej miary kąta, zwanej też miarą radialną lub analityczną, jednostką główną jest radian , tzn. kąt płaski zawarty między dwoma promieniami koła, wycinającymi z okręgu tego koła łuk o długości równej promieniowi. Wprawdzie według międzynarodowego układu jednostek miar SI kąt ten określa się skrótem „rad”, będziemy jednak nadal używać oznaczenia , ponieważ to oznaczenie nadal jest wykorzystywane do licznych wzorów, co mogłoby prowadzić do nieporozumień, a nawet błędów. Według matematycznej definicji ![]()
jest to stosunek łuku do promienia r:
![]()
= ł:r .(1.6)
Kątowi pełnemu odpowiada 2 radianów.
Rys.1.1
Łukowa miara kąta ma szerokie zastosowanie nie tylko w matematyce, ale również w zagadnieniach geodezyjnych, zwłaszcza w rachunkach dokładnościowych.
1.3.2. Zamiana wartości kątów
Ze względu na konieczność korzystania z instrumentów pomiarowych posiadających różne systemy miar kątowych, występuje nieraz w praktyce potrzeba przeliczenia wartości kątów z jednego podziału na drugi. Aby przejść ze jednej miary na drugi i odwrotnie, wystarczy zapamiętać podstawową zależność:
![]()
; (1.7)
łatwo bowiem wówczas wyprowadzić wzory zamienne.
A. Zamiana stopni na grady i odwrotnie
Jeżeli przez oznaczymy kąty wyrażone w mierze stopniowej, a przez - te same kąty, ale wyrażone w mierze gradowej, to możemy napisać następujące oczywiste zależności:
![]()
(1.8)
![]()
(1.9)
![]()
(1.10)
a z nich wypływają następujące dwa szeregi wzorów:
![]()
![]()
![]()
![]()
![]()
![]()
PRZYKŁAD 1. Przedstawić kąt = 242142 w mierze gradowej.
g = 241,1111111g + 211,85185c + 423,086cc = 27,06852g
PRZYKŁAD 2. Przedstawić kąt = 27,0685g w mierze stopniowej.
= 0,927,0685g = 24,36165.
Aby wyrazić wartość kąta w układzie sześćdziesiątkowym, trzeba dokonać jeszcze przeliczenia ułamka dziesiętnego, wyrażającego części stopnia (tj....,36165) na minuty i sekundy.
24,36165 -zapisujemy 24 a resztę, tj.0,36165 poddajemy dalszym przeliczeniom; 0,3616560= 21,699 -zapisujemy 21, resztę tj.0,699 poddajemy dalszym przeliczeniom;0.69960= 41,94. Ostateczna wartość kąta = 242141,94.
Istnieje wiele sposobów przeliczenia kątów z miary stopniowej na gradową i odwrotnie.
B. Zamiana stopni na tysięczne i odwrotnie
Przy identycznym toku rozumowania, jak to przeprowadzono wyżej, znajdziemy:
![]()
![]()
![]()
![]()
![]()
![]()
PRZYKŁAD 3. Przedstawić kąt = 242142 w mierze tysięcznej.
tys = 2416.6667+210,2778+420,00463 = 04-06,0291.
PRZYKŁAD 4. Przedstawić kąt = 04-06,0291 w mierze kątowej.
= 0406,02910.06 = 24,3617 = 242142,1.
C. Związek miary stopniowej z miarą czasową
W mierze czasowej za jednostkę przyjmuje się jeden pełny obrót Ziemi dokoła własnej osi, nazywając go dobą. Części pełnego obrotu wyraża się w godzinach, minutach i sekundach, które w tym przypadku mają znaczenie kątów, a nie jednostek miary czasu. Jeżeli dobę podzielimy na 24 godziny, a dalej - zgodnie z systemem sześćdziesiątkowym - ustalimy mniejsze jednostki w postaci minut i sekund miary czasowej kąta, to otrzymamy niezwykle prostą i dogodną zależność z miarą stopniową kąta. Oto ona:
360 = 1d
1 = ![]()
![]()
![]()
![]()
![]()
![]()
D. Zamiana stopni na radiany i odwrotnie
Z relacji, wynikającej z definicji miary łukowej i stopniowej, wyprowadzić można związek pomiędzy obiema miarami
![]()
(1.11)
![]()
(1.12)
Oznaczając wyrażenie ułamkowe literą otrzymamy odpowiednio:
![]()
![]()
![]()
Współczynniki noszą nazwę współczynników zamiany miary łukowej na stopniową. Współczynnik oznacza liczbę stopni, minut lub sekund, jakie się mieszczą w jednym radianie.
![]()
![]()
![]()
![]()
![]()
![]()
E. Zamiana gradów na tysięczne i odwrotnie
Wychodząc ze wzoru (1.7) otrzymujemy:
![]()
![]()
![]()
![]()
![]()
![]()
PRZYKŁAD 5. Przedstawić kąt = 27,0685g w tysięcz-
nych.
27,0685g00-15 = 04-06,0275
PRZYKłAD 6. Wyrazić kąt 04-06,028 w mierze gradowej.
04-06,0280,0666667g = 27,0685g
F. Związek pomiędzy miarą gradową a łukową
Do zamiany miary łukowej na gradową i odwrotnie wykorzystuje się współczynniki otrzymując następujące zależności:
![]()
![]()
![]()
![]()
![]()
![]()
gdzie
![]()
![]()
![]()
G. Zamiana tysięcznych na miarę łukową i odwrotnie
Do zamiany wykorzystuje się zależność 2 = 60-00. Z niej otrzymujemy:
00-01 = ![]()
![]()
PRZYKłAD 7. Przedstawić kąt 04-06,03 w mierze łukowej.
04-06,030,00104720 = 0,425195 rad.
PRZYKŁAD 8. Przedstawić kąt 0,425195 rad w tysięcznych.
0,42519509-54,92 = 04-06,03.
1.3.3. Funkcje trygonometryczne małych kątów
W analizie matematycznej udowadnia się, że funkcje trygonometryczne można rozwinąć na następujące szeregi potęgowe:
![]()
(1.13)
![]()
(1.14)
![]()
(1.15)
Kąt ![]()
, występujący po prawej stronie powyższych równań, jest wyrażony w mierze analitycznej (łukowej).
Powyższe rozwinięcia wydają się być bardzo dogodne przy pracach rachunkowych, ale pod warunkiem, że można się ograniczyć do wyrazów w drugiej potędze. Przy takim założeniu powyższe wzory przyjęłyby następującą postać:
![]()
![]()
![]()
![]()
Jasną jest rzeczą, że na skutek odrzucenia dalszych wyrazów rozwinięcia, wzory nie dają ścisłych wartości funkcji trygonometrycznych, lecz wartości przybliżone. Im większy będzie kąt , tym większą wartość będą reprezentować wyrazy odrzucone, a co za tym idzie, z tym mniejszą dokładnością wyznaczone zostaną funkcje trygonometryczne.
Trzeba więc założyć z góry pewną dokładność, z jaką należy obliczyć wartości funkcji trygonometrycznych, a wówczas będzie można określić maksymalne wartości kątów, stanowiących granicę stosowalności tych wzorów.
W odrzuconych wyrazach dominujące znaczenie posiada zawsze pierwszy z wyrazów odrzuconych, gdyż jest w każdym przypadku wielkością o dwa rzędy większą, niż następny z kolei wyraz odrzucony. Dalej zauważamy, że wśród dominujących, największą wartość przedstawia drugi wyraz wzoru (1.15), tj. ![]()
, gdyż wyraźnie przewyższa pierwsze odrzucone wyrazy wzorów (1.14) i (1.13). Nie ulega bowiem wątpliwości, że jest
![]()
Wobec tego wystarczy, aby sprawdzianem nieprzekroczenia założonej dokładności był wyraz ![]()
. Kierujemy się przy tym następującym rozumowaniem: Funkcje trygonometryczne używane są najczęściej przy ocenie dokładności oraz obliczeniach współrzędnych, gdzie oblicza się charakterystyczne iloczyny, których składnikami są bok (długość liniowa) i jedna z funkcji trygonometrycznych. Zakłądając średnią długość boku mierzonego taśmą d=150 m, a błąd pomiaru taśmą rzędu 1 cm, postawimy sobie warunek, aby błąd z tytułu uproszczonego obliczania funkcji trygonometrycznej, nie wpłynął na obliczenie wspomnianego iloczynu w stopniu większym niż błąd pomiaru taśmą, to można uważać takie uproszczone obliczanie funkcji trygonometrycznej za uzasadnione, za wystarczająco dokładne.
Przechodząc do matematycznego zapisu powyższego wywodu notujemy
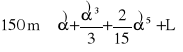
,
który pragniemy zastąpić wyrażeniem
![]()
,
z tym jednakże zastrzeżeniem, aby pierwszy odrzucony wyraz był mniejszy od 1 cm, czyli, aby
![]()
.
Rozwiązjąc tę nierówność otrzymujemy kolejno:
![]()
a następnie
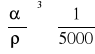
dalej
![]()
i wreszcie
![]()
.
W wyniku naszych rozważań otrzymaliśmy rezultat, który nas poucza, że dla kątów mniejszych niż 321 można stosować wzory uproszczone w miejsce wzorów ścisłych, a powstały z tego tytułu błąd nie przekroczy błędu pomiaru.
W tej sytuacji można przyjąć, że funkcje trygonometryczne małych kątów, tzn. kątów nie większych niż 3, można obliczać ze wzorów przybliżonych:
![]()
, (1.16)
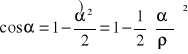
, (1.17)
![]()
, (1.18)
![]()
. (1.19)
Wzory otrzymane drogą analityczną, dadzą się również przedstawić w formie poglądowej, np. na rys. 1.2.
Rysunek 1.2 należy rozpatrywać pod kątem następujących założeń:
1) kąt środkowy jest kątem małym;
2) promień koła jest róny jedności, r=1.
Rys. 1.2
Na podstawie rysunku i powyższych założeń można napisać:
![]()
![]()
![]()
Z rysunku widaćdalej, że wprawdzie s![]()
t, ale dla małych kątów będzie można przyjąć, że
![]()
(1.20)
Zależności (1.20) są identyczne z uprzednio wyprowadzonymi wzorami (1.16) i (1.18).
Zastosowanie wzorów uproszczonych na obliczenie funkcji trygonometrycznych małych kątów przeprowadzimy na kilku przykładach.
PRZYKŁAD 1. Ile wynosi sin 146?
Zgodnie z wzorem (1.16) mamy
![]()
,
a ponieważ 146 = 106, więc
sin 146 ![]()
=0,0308
PRZYKŁAD 2. Ile wynosi kąt x , jeżeli tgx = 0,0444?
Zgodnie z wzorem (1.18) mamy
x = tgx ,
czyli
x = 0,04443438 = 152,6=232,6.
PRZYKłAD 3. Ile wynosi cos 245?
Zgodnie zwzorem (1.17) i uwzględnieniem wartości, danych w zadaniu, piszemy
cos 245 = 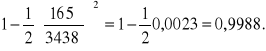
PRZYKŁAD 4. Ile wynosi , jeżeli ctg = 37,5?
Zgodnie z wzorem (1.19) piszemy wprost
![]()
= 131,8.
Wyszukiwarka