Układy równań liniowych
Układem ![]()
równań liniowych z ![]()
niewiadomymi ![]()
, gdzie ![]()
, nazywamy układ postaci
![]()
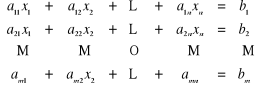
,
gdzie ![]()
, ![]()
dla ![]()
, ![]()
.
Rozwiązaniem układu równań liniowych nazywamy każdy ciąg ![]()
liczb rzeczywistych spełniających ten układ .
Układ równań , który nie ma rozwiązania , nazywamy układem sprzecznym .
Uwaga . Powyższy układ ![]()
można zapisać w postaci macierzowej :
![]()
![]()
,
gdzie
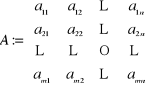
, 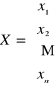
, 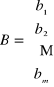
.
Gdy ![]()
, to układ nazywamy jednorodnym .
Jednym z rozwiązań układu jednorodnego jest macierz zerowa 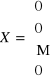
.
Gdy ![]()
, układ nazywamy układem niejednorodnym .
Gdy macierz ![]()
jest macierzą kwadratową nieosobliwą ( tzn. ![]()
i ![]()
) , to układ ![]()
nazywamy układem Cramera .
Twierdzenie . Układ Cramera ![]()
ma dokładnie jedno rozwiązanie . Rozwiązanie to jest dane wzorem :
![]()
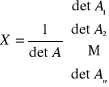
,
gdzie ![]()
oznacza stopień macierzy ![]()
, natomiast ![]()
dla ![]()
oznacza macierz ![]()
, w której ![]()
kolumnę zastąpiono kolumną wyrazów wolnych ![]()
.
Przykład . Rozwiązać układ równań :
(1) 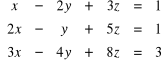
.
Oznaczamy : 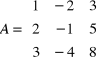
, 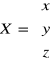
, ![]()
. Zatem układ (1) w postaci macierzowej ma postać : ![]()
.
Mamy
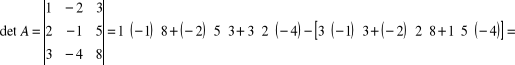
![]()
![]()
.
Zatem układ ten jest układem Cramera . Ma on zatem dokładnie jedno rozwiązanie . Wyznaczamy teraz
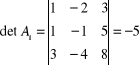
, 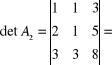
![]()
, 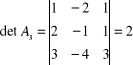
.
Na podstawie wzorów ![]()
mamy : ![]()
, ![]()
, ![]()
.
(2) 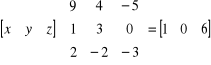
.
Z własności transpozycji macierzy wiemy , że ![]()
. Stąd
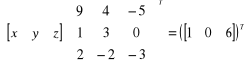
, czyli 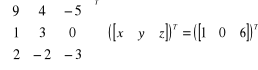
.
Zatem układ (2) możemy zapisać w postaci :
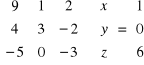
.
Korzystamy ze wzorów (i) :
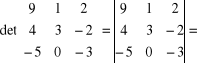
![]()
, 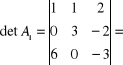
![]()
, 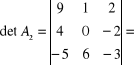
![]()
,
![]()
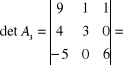
![]()
.
Rozwiązaniem układu są liczby : ![]()
, ![]()
, ![]()
.
Metoda eliminacji Gaussa dla układów Cramera
Niech ![]()
będzie układem Cramera , w którym ![]()
jest macierzą stopnia ![]()
. Rozwiązanie tego układu znajdujemy w następujący sposób :
1. budujemy macierz rozszerzoną układu postaci
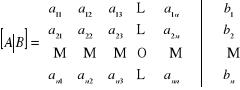
;
2. przekształcamy macierz rozszerzoną do postaci ![]()
wykonując na jej wierszach ! następujące operacje elementarne :
(a) zamianę między sobą dwóch dowolnych wierszy ;
(b) pomnożenie dowolnego wiersza przez liczbę różną od zera ;
(c) dodanie do elementów dowolnego wiersza odpowiadających im elementów innego wiersza pomnożonych
przez dowolną liczbę .
Operacje te mają na celu doprowadzenie macierzy rozszerzonej do postaci :
![]()
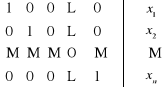
.
Ostatnia kolumna macierzy rozszerzonej ( macierz ![]()
) jest wtedy rozwiązaniem wyjściowego układu równań .
Twierdzenie Kroneckera - Capellego
Układ równań liniowych ![]()
ma rozwiązanie wtedy i tylko wtedy , gdy rząd macierzy ![]()
jest równy rzędowi macierzy rozszerzonej ![]()
tego układu ;
![]()
.
Fakt . Niech ![]()
będzie układem równań liniowych z ![]()
niewiadomymi . Wówczas :
1. jeżeli ![]()
, to układ nie ma rozwiązania ( układ jest sprzeczny ) ;
2. jeżeli ![]()
, to układ ma dokładnie jedno rozwiązanie ( jest oznaczony ) ;
3. jeżeli ![]()
, to układ ma nieskończenie wiele rozwiązań zależnych od ![]()
parametrów ( jest nieoznaczony ) .
Przykład . W podanych układach określić liczbę rozwiązań :
a) 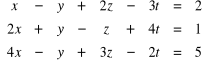
.
Wyznaczamy a następnie porównujemy rzędy macierzy ![]()
i macierzy rozszerzonej ![]()
:
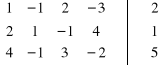
![]()
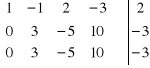
![]()
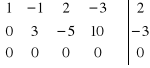
Otrzymaliśmy macierze o dwóch schodkach ( maciach układu ![]()
i macierz rozszerzona ) . Ponieważ ![]()
więc układ ma nieskończenie wiele rozwiązań ( jest nieoznaczony ) zależnych od 4-2=2 parametrów .
b) 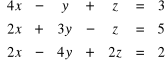
.
![]()
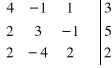
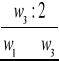
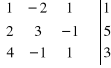
![]()
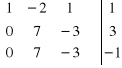
![]()
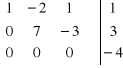
. Zauważmy , że ![]()
, ![]()
. Ponieważ ![]()
, więc układ
jest sprzeczny ( nie ma rozwiązań ) .
3
Wyszukiwarka