1. Wstęp teoretyczny.

1. Drgania oscylatora harmonicznego.

Z punktu widzenia matematyki ruch harmoniczny punktu materialnego opisuje równanie:

gdzie:

x- oznacza wychylenie punktu drgającego od położenia równowagi,

t - czas,

A i
- to wielkości stałe w danym ruchu, tzn. niezależnie od czasu. Znaczenie A wynika z charakteru funkcji sinus: funkcja ta może się zmieniać w granicach od -1 do +1, a zatem wychylenie x może się zmieniać w granicach -A
+A. Stała A oznacza więc największe wychylenie od położenia równowagi, zwane amplitudą.

- częstotliwość kołowa

Powyższy związek wynika z następującego rozumowania :

Okres funkcji sinus wynosi 2
. Jeżeli czas t wzrośnie o okres T, to argument
funkcji sinus wzrośnie o 2
, zatem

Prędkość w ruchu harmonicznym jest pochodną drogi po czasie
prędkość jest wielkością zmienną okresową ponieważ -1
, więc najwyższa wartość prędkości

Przyśpieszenie jest pochodną prędkości względem czasu:

ale iloczyn
wyraża wychylenie (x) od położenia równowagi , a zatem

lub

Przyśpieszenie w ruchu harmonicznym jest proporcjonalnie do wychylenia ze stanu równowagi.

DRGANIA NIEGASNĄCE

Drgania swobodne dotyczą układów zamkniętych, wzbudzane w chwili początkowej drgające swobodnie bez działania sił wewnętrznych. Jeśli układ wykonuje drgania normalne tylko jednej postaci , wówczas na jednostkę masy każdego z poruszających się elementów działa taka sama siła kierująca , zatem wszystkie elementy układu oscylują wtedy według tej samej zależności czasowej
tzn. z jednakową częstotliwością
i jednakowym przesunięciem fazowym

DRGANIA TŁUMIONE

Jeżeli drgania odbywają się w ośrodku materialnym, to wskutek występowania siły oporu ośrodka drgania te będą zanikać, drgania takie będziemy nazywać tłumionymi. Siłę oporu ośrodka nazwiemy siłą tłumiącą F_t siła tłumiąca jest proporcjonalna do prędkości ciała drgającego jeżeli prędkość ta jest niewielka.

b- współczynnik oporu

Według II zasady dynamiki Newtona :

uwzględniając siłę tłumiącą możemy zapisać :

k- współczynnik sprężystości

x- wychylenie z położenia równowagi

b- współczynnik oporu

a- przyśpieszenie

Podstawiając do wzoru otrzymamy :

/*

równanie różniczkowe drgań tłumionych, którego rozwiązaniem jest funkcja:

- współczynnik tłumień

- pulsacja drgań tłumionych

- faza drgań

DRGANIA WYMUSZONE

Aby opory ośrodka nie tłumiły drgań to na drgający punkt materialny należy działać odpowiednio zmienną siłą. Siłę tą będziemy nazywać siłą wymuszającą F_w.

- pulsacja z jaką zmienia się siła wymuszająca

F₀ - amplituda siły wymuszonej

Według II zasady dynamiki Newtona :

Uwzględniając działające siły mamy :

k- współczynnik sprężystości

x- wychylenie z położenia równowagi

b- współczynnik oporu

a- przyśpieszenie

Otrzymamy równanie różniczkowe drgań wymuszonych :

rozwiązaniem jest funkcja :

gdzie: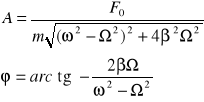

Widzimy, że w wyniku działania siły wymuszającej F_w pkt. materialny wykonuje drgania harmoniczne z pulsacją
.

2. Wahadła fizyczne jako oscylatory harmoniczne.

Ruch drgający może wykonywać każde ciało sztywne zawieszone tak, aby mogło poruszać się wokół stałej osi O, która nie przechodzi przez jego środek masy S. Ciało takie będziemy nazywać wahadłem fizycznym. Wahadło fizyczne różni się od matematycznego tym, że ma dowolny rozkład masy.

O

h

s

S

G

Ruch wahadła fizycznego podlega drugiej zasadzi dynamiki dla ruchu obrotowego wokół stałej osi , czyli

Gdzie: M jest momentem siły powodującej ruch względem osi przechodzącej przez punkt zawieszenia, J- momentem bezwładności względem tej osi,
- przyśpieszeniem kątowym. Siłą działającą na wahadło jest siła ciężkości G zaczepiona w środku masy S. Stąd na podstawie rysunku, mamy

Wartość liczbowa wektora momentu obrotowego M wynosi więc

gdzie m jest masą,
zaś kątem wychylenia wahadła. Znak minus, który pojawił się w powyższym wzorze, pochodzi stąd, że moment obrotowy M jest skierowany przeciwnie niż wektor reprezentujący wychylenie.

Drugą zasadę dynamiki dla ruch obrotowego wokół stałej osi możemy też napisać w postaci skalarnej

Dla małych kątów wychylenia wahadła
, wobec czego

a ponieważ

stąd

Podstawmy teraz
; otrzymamy wówczas równanie różniczkowe ruchu harmonicznego dla wahadła fizycznego

Przy czym wielkością, która drga harmonicznie, jest kąt wychylenia
. ponieważ droga środka masy
, więc ruch środka masy po łuku jest także ruchem harmonicznym, podobnie jak ruch dowolnego punktu wahadła fizycznego.

Moment siły
(w mierze łukowej) nazywamy momentem kierującym i oznaczamy przez

Równanie różniczkowe ruchu harmonicznego wahadła możemy zatem napisać w postaci

Ponieważ
, stąd na okres drgań wahadła fizycznego przy niewielkich wychyleniach otrzymujemy wyrażenie

3. Zastosowanie wahadła torsyjnego do wyznaczania modułu sztywności.

Wahadło torsyjne to krążek zawieszony w środku masy. Drut na którym wisi krążek zamocowany jest sztywno z obydwu stron. Jeżeli krążek obrócimy w płaszczyźnie poziomej z położenia równowagi, to drut zostanie skręcony. Wtedy na krążek działa moment siły skręconego drutu i stara się przywrócić krążek do położenia równowagi. Moment ten jest proporcjonalny do wielkości skręcenia, czyli do kątowego przemieszczenia (prawo Hooke'a), zatem

Stała x zależy od właściwości drutu, nazywamy ją stałą skręcenia albo momentem kierującym. Znak minus wskazuje, że moment siły ma zwrot przeciwny niż przemieszczenie kątowe θ. Powyższe równanie określa warunki, przy których zachodzi kątowy ruch harmoniczny prosty.

Równanie ruchu dla wahadła torsyjnego ma postać

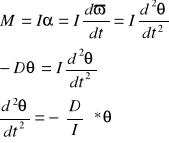
Równanie dla kątowego ruchu harmonicznego prostego jest podobne do równania dla liniowego ruchu harmonicznego prostego.

Okres drgań wynosi

Znając x i mierząc RT możemy wyznaczyć moment bezwładności drgającego ciała sztywnego. Natomiast znając I i mierząc T mamy możliwość wyznaczenia stałej x dla dowolnego materiału.

4. Właściwości sprężyste ciał stałych. Rodzaje odkształceń. Prawo Hooke'a i granice jego stosowalności.

Wyróżniamy kilka rodzajów odkształceń sprężystych. Odkształcenia mogą mieć różny charakter. Można tu wymienić wydłużenia (skrócenia), rozszerzenia objętościowe (skurczenia), zgięcia, skręcenia itp.

Za miarę odkształcenia związanego ze zmianą długości przyjmujemy względny przyrost długości ε, zdefiniowany jako przyrost długości Δl do długości pierwotnej l₀:

Prawo Hooke'a to prawo doświadczalne i obowiązujące dla małych odkształceń. Prawo to mówi, że stosunek naprężenia do związanego z nim odkształcenia jest wielkością stałą dla danego materiału. Stosunek ten nazywamy modułem sprężystości.

Prawo Hooke'a przy wydłużeniach wyraża się wzorem

,

gdzie σ oznacza ciśnienie (naprężenie) normalne, E - moduł sprężystości przy wydłużeniu, zwany modułem Younga.

Idealne odkształcenie objętościowe występuje tylko wtedy, gdy kształt ciała zostaje zachowany, natomiast gęstość ulega zmianie (np. ciało kuliste pozostaje ciałem kulistym, ale ma inną objętość). Za miarę odkształcenia objętościowego przyjmujemy względny przyrost objętości θ zdefiniowany jako stosunek przyrostu objętości ΔV do objętości pierwotnej V₀:

W odniesieniu do odkształceń objętościowych prawo Hooke'a możemy napisać w postaci

,

gdzie K - moduł sprężystości objętościowej.

Z idealnym odkształceniem postaciowym mamy do czynienia wtedy, gdy gęstość dowolnie małego elementu ciała pozostaje niezmienna, a zmianie ulega kształt. Za miarę tego odkształcenia przyjęto tangens kąta zawartego pomiędzy pierwotnym położeniem ściany na którą podziałała siła a tą samą ścianą w pozycji odchylonej. Prawo Hooke'a wyraża się wzorem

,

gdzie G - moduł sprężystości postaciowej.

Granice stosowalności prawa Hooke'a

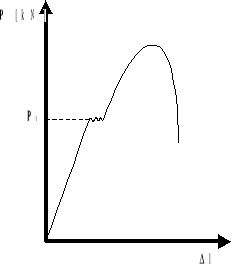
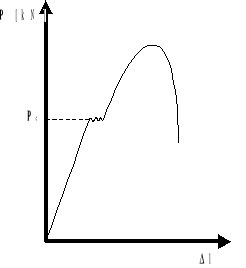
Dla naprężeń rosnących stopniowo od zera otrzymuje się na wykresie odcinek linii prostej (do punktu P_e), odpowiadający prostej proporcjonalności między naprężeniem i wydłużeniem. Odcinek ten odpowiada zakresowi dokładnej stosowalności prawa Hooke'a. Wartość naprężenia będącą rzędną punktu P_e nazywamy granicą proporcjonalności. Jest to maksymalne naprężenie, przy którym stosuje się jeszcze prawo Hooke'a. Stosowanie ciśnień większych odpowiada gwałtowniejszemu wzrostowi przyrostów długości, co dalej powoduje powstanie przewężenia, w którym po przekroczeniu granicy wytrzymałości ciała następuje zerwanie.

5. Wyprowadzenie wzoru roboczego.

Współczynnik sztywności cienkich prętów można wyznaczyć metodą dynamiczną. Na drucie o długości l i średnicy 2r mocujemy bryłę sztywną (wibrator) o momencie bezwładności
. Jeżeli wibrator skręcimy w płaszczyźnie poziomej o kąt
to pręt skręci się o ten sam kąt i wskutek tego powstaje w pręcie moment obrotowy sił sprężystych.

l

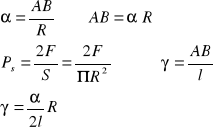
Z prawa Hookea

Powstałe pod wpływem sił zewnętrznych skręcenie wywołuje w pręcie siły oporu, które powodują powstanie momentu obrotowego równego co do wielkości momentu sił zewnętrznych lecz przeciwnie
skierowanego
. Siły te po oswobodzeniu wibratora będą wprowadzały go , a ruch drgający o okresie
gdzie
. Mierząc czas i znając I,
( momenty bezwładności tarcz , I- moment tarczy dodatkowej ) mamy:

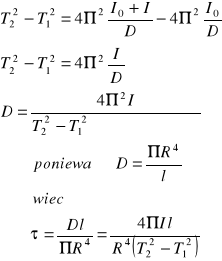
2. Obliczenia

Moduł skręcający τ obliczono ze wzoru

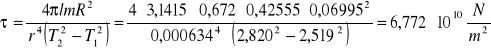
3. Rachunek błędów

Błędy pomiaru okresów drgań ΔT₁ oraz ΔT₂ obliczono ze wzoru Gaussa na błąd średni kwadratowy wartości średniej.

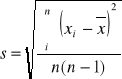
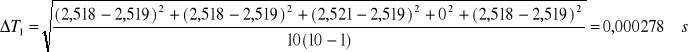
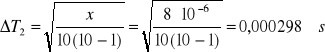
Błąd pomiaru Δr również obliczono ze wzoru Gaussa.

Błąd modułu sztywności wyznaczono metodą pochodnej logarytmicznej.

4. Dyskusja i wnioski

Po porównaniu mojego wyniku z wynikami z „Tablic matematyczno - fizycznych” Władysława Wojtowicza doszedłem do wniosku, że drut na którym wykonywałem doświadczenie wykonany był ze stali. Na wartość wyniku duży wpływ mógł mieć wiek drutu na którym wykonywane było doświadczenie. Również nieduże odchyły od pionu podczas oscylacji mogły w niewielkim stopniu wpłynąć na dokładność pomiarów. Wydaje mi się, że duża wartość błędu powoduje nieprzydatność tego doświadczenia do precyzyjnego ustalania rodzaju materiału.

---