Obliczenie krzywych interakcji MRd - NRd
Przykład liczbowy
Beton C30/37
![]()
Stal St500b
![]()
![]()
![]()
‰
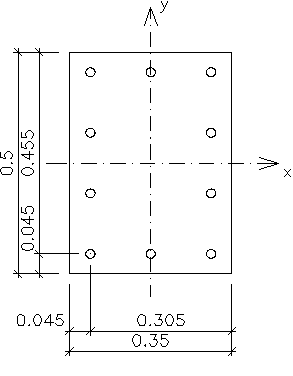
Pręty o średnicy 16mm
As = 2,01cm2 (pole przekroju pojedynczego pręta)
Nośność przekroju w płaszczyźnie y
![]()
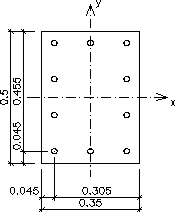
Przyjęto ξ = 2,5 i model betonu paraboliczno - prostokątny (1)
Obliczamy na podstawie odpowiednich wzorów lub odczytujemy z tablicy odkształcenia i obliczamy pozostałe (jak na rysunku) oraz odczytujemy ω = 1,0329
i ζ = 0,481
Jeżeli εs ≥ εyd to σ = fyd ; w przeciwnym razie σ = εs×Es
Fs1 = As1×εs1×Es = 3×2,01×10-4×1,46×10-3×200×106 = 176,1kN
Fs2 = As2×fyd = 3×2,01×10-4×435×103 = 262,3kN
Fs3 = As3×εs3×Es = 2×2,01×10-4×1,79×10-3×200×106 = 143,9kN
Fs4 = As4×εs4×Es = 2×2,01×10-4×2,06×10-3×200×106 = 165,6kN
Fc = ωbdfcd = 1,0329×0,35×0,455×21430 = 3525,0kN
NRd = ΣN = 4272,9kN
Ramię sił wewnętrznych
z = ζd = 0,481×0,455 = 0,219m
Obliczamy nośność MRd jako sumę momentów sił względem osi x
MRd = 262,3×0,205 + 165,6×0,065 + ![]()
- 143,9×0,065 - 176,1×0,205 =
= 68,43kNm
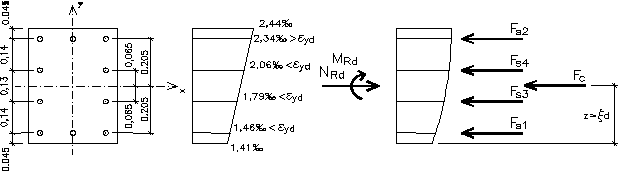
Osiowe ściskanie
We wszystkich prętach zbrojenia
σs = 2,00×10-3×200×106 = 400MPa
Współczynnik ω = 1,1
NRd,max = 10×2,01×10-4×400×103 + 1,1×0,35×0,455×21430 =
= 804,0 + 3754,0 = 4558,0kN
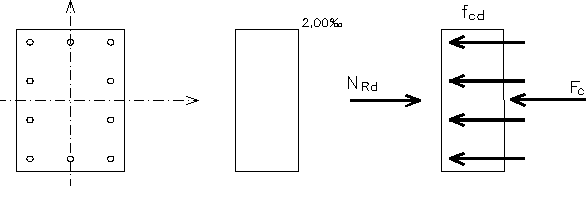
Osiowe rozciąganie
We wszystkich prętach zbrojenia σs = 435MPa, beton niczego nie przenosi.
NRd,min = -10×2,01×10-4×435×103 = -874,3kN
Wyszukiwarka