Hydroliza

wg teorii Arrheniusa:

- reakcja przebiegająca między wodą a solami:

- słabych kwasów i mocnych zasad,

- mocnych kwasów i słabych zasad,

- słabych kwasów i słabych zasad.

wg teorii Brönsteda:

- szczególny przypadek reakcji protolitycznej czyli reakcji typu kwas - zasada, przebiegającej w rozpuszczalniku protycznym,

- reakcje protolityczne słabych kwasów i słabych zasad, przy czym biorą w nich udział kwasy i zasady obdarzone ładunkiem elektrycznym.

Równania reakcji hydrolizy. Typy reakcji hydrolizy:

a) Sole słabych jednoprotonowych kwasów i mocnych jednoprotonowych zasad, np.: KCN, CH₃COONa, NaNO₂, HCOONa

Przykład: NaNO₂

dysocjacja:

hydroliza:

Odczyn wodnych roztworów takich soli - zasadowy

b) Sole słabych jednoprotonowych zasad i mocnych jednoprotonowych kwasów, np. NH₄Cl, NH₄NO₃ i inne.

Przykład: NH₄NO₃

dysocjacja:

hydroliza:

Odczyn wodnych roztworów takich soli - kwasowy

c) Sole słabych jednoprotonowych kwasów i słabych jednoprotonowych zasad, np. HCOONH₄, CH₃COONH₄, NH₄NO₂, NH₄CN i inne.

Przykład: NH₄NO₂

dysocjacja:

hydroliza:

Odczyn wodnych roztworów takich soli - obojętny, kwasowy lub zasadowy w zależności od wartości stałych dysocjacji odpowiednich kwasów i zasad.

Hydroliza soli wieloprotonowych kwasów i wieloprotonowych zasad przebiega wielostopniowo (podobnie jak proces dysocjacji).

Typy soli ulegających hydrolizie:

a) Sole słabych dwuprotonowych kwasów i mocnych jednoprotonowych zasad, np.: Na₂S, Na₂CO₃.

Hydroliza praktycznie tylko w pierwszym stopniu, tworzące się jony OH- cofają drugi stopień hydrolizy.

Przykład: Na₂S

dysocjacja:

hydroliza:

Odczyn wodnych roztworów - zasadowy

b) Sole trójprotonowych kwasów i mocnych jednoprotonowych zasad, np.: KH₂PO₄, K₂HPO₄, K₃PO₄.

Odczyn wodnych roztworów - kwasowy lub zasadowy, w zależności od rodzaju soli, np.:

- KH₂PO₄

dysocjacja:

hydroliza:

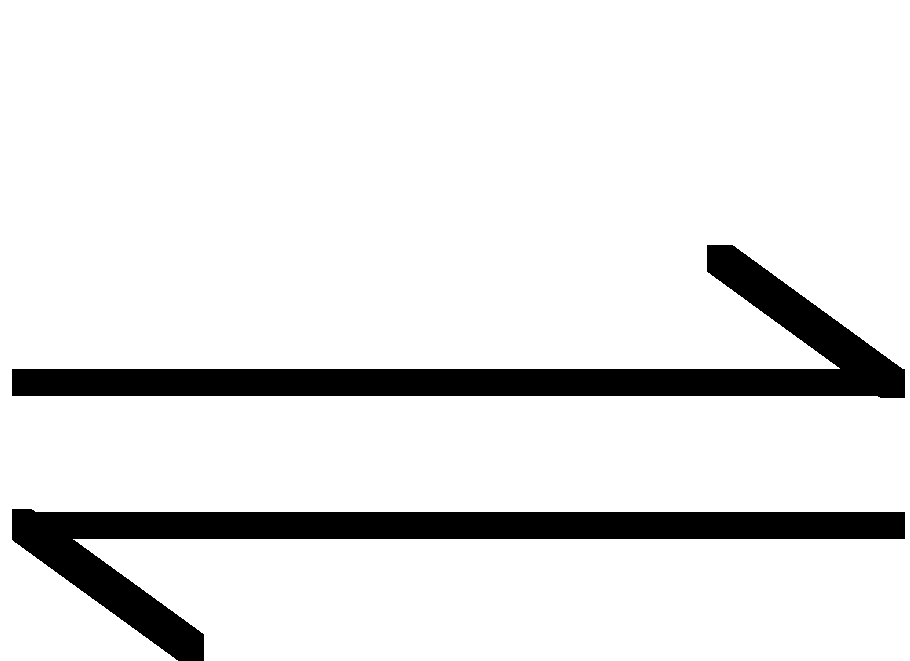
odczyn roztworu wodnego - słabo kwasowy

- K₂HPO₄

dysocjacja:

hydroliza:

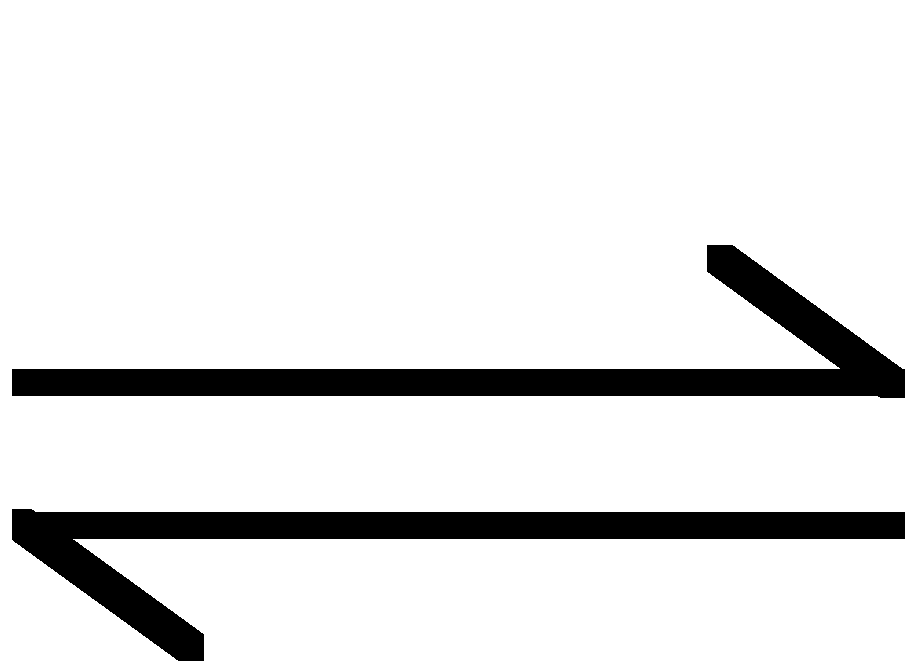
odczyn roztworu wodnego - słabo zasadowy

- K₃PO₄

dysocjacja:

hydroliza:
+ H₂O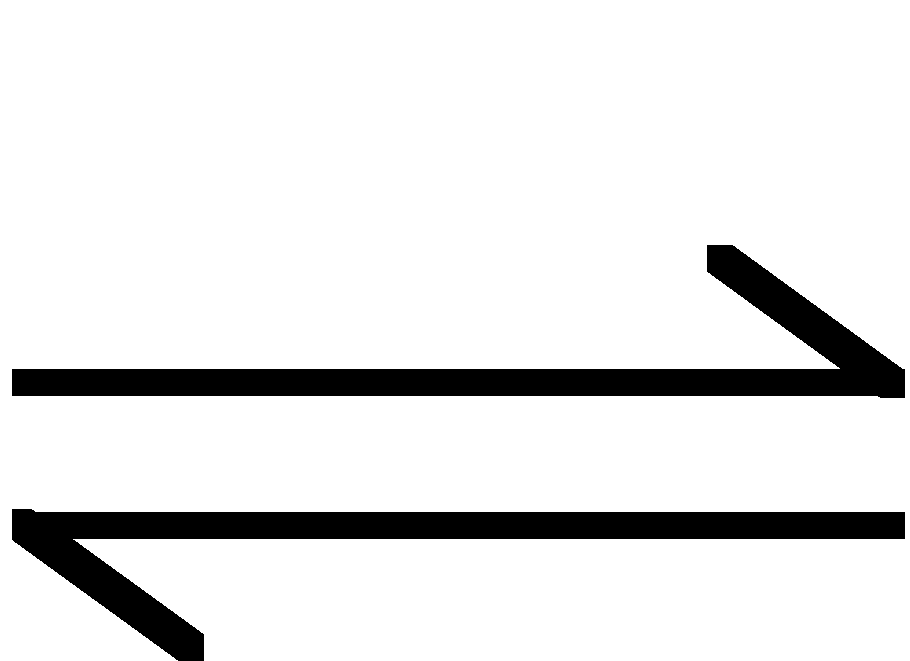

+

+ H₂O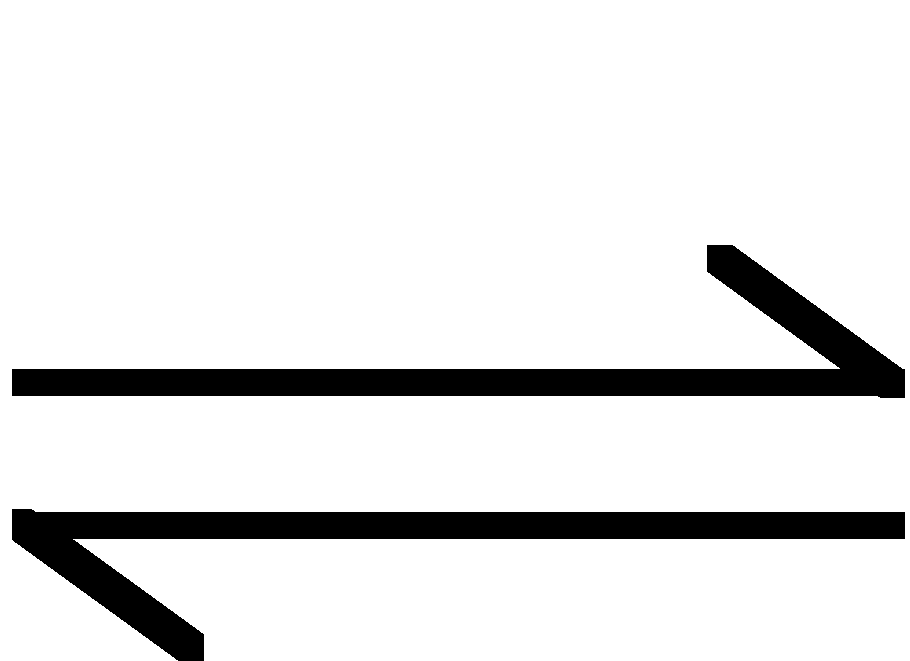

+

ostatnia reakcja - nie zachodzi (nadmiar jonów OH-)

odczyn roztworu wodnego - zasadowy

c) Sole mocnych jednoprotonowych lub dwuprotonowych kwasów i słabych jednoprotonowych lub wieloprotonowych zasad, np.: MgCl₂, AlCl₃, FeCl₃, NiSO₄, CuSO₄, Al₂(SO₄)₃ itp.

Przykłady:

+ 2 H₂O

+

+ 2 H₂O

+

+ 2 H₂O

+

Odczyn wodnych roztworów takich soli - kwasowy.

Hydroliza przebiega z reguły jednostopniowo ponieważ:

- nadmiar jonów
nie dopuszcza do utworzenia zasady,

- tworzące się sole zasadowe są trudno rozpuszczalne i opuszczają środowisko reakcji.

d) Sole słabych jedno- lub wieloprotonowych kwasów i słabych jedno- lub wieloprotonowych zasad, np.: (NH₄)₂S, (NH₄)₂CO₃.

Przykład:

Odczyn wodnych roztworów takich soli - obojętny, kwasowy lub zasadowy w zależności od wartości stałych dysocjacji odpowiednich kwasów i zasad.

e) Sole bardzo słabych zasad i kwasów - hydroliza prowadzi do odtworzenia słabej zasady i słabego kwasu, np. Al₂S, Cr₂S₃ itp.

Przykład 1. Które z wymienionych soli ulegają hydrolizie: K₂CO₃, KCl, KCN, KBr, NaNO₂, HCOOK, Al₂(SO₄)₃, Na₂S, K₂SO₄, (NH₄)₂S, (NH₄)₃, NaNO₃, ZnCl₂, CuSO₃, NaClO₄, FeSO₄, Mg(ClO₄)₂, KIO₃, CrCl₃, CuBr₂? Podać odczyn wodnych roztworów hydrolizujących soli.

Hydroliza wg teorii Brönsteda:

- szczególny przypadek reakcji protolitycznej czyli reakcji typu kwas - zasada, przebiegającej w rozpuszczalniku protycznym,

- reakcje protolityczne słabych kwasów i słabych zasad, przy czym biorą w nich udział kwasy i zasady obdarzone ładunkiem elektrycznym.

Zatem, w roztworze:

a) mogą być obecne jony o przeciwnym znaku, nie wykazujące właściwości kwasowo-zasadowych, które w samej reakcji protolitycznej nie biorą udziału. Jony takie to:

- kationy litowców i niektórych berylowców,

- aniony mocnych kwasów: Cl-, Br-,

.

- np.:

w wodnym roztworze mrówczanu sodu:

HCOONa → HCOO- + Na⁺

tworzą się:

- jony HCOO^- - zasada obdarzona ładunkiem,

- jony Na+ - jon o przeciwnym znaku, nie wykazujący właściwości kwasowo-zasadowych,

lub:

w wodnym roztworze chlorku amonu:

tworzą się:

- jony
- kwas obdarzony ładunkiem,

- jony Cl^- - jon o przeciwnym znaku, nie wykazujący właściwości kwasowo-zasadowych,

b) mogą być obecne jony o przeciwnym znaku, wykazujące właściwości kwasowo-zasadowe, które biorą udział w równoległej reakcji protolitycznej.

np.:

w wodnym roztworze mrówczanu amonu:

HCOONH₄ → HCOO- +

tworzą się:

- jony HCOO^- - zasada obdarzona ładunkiem

- jony
- kwas obdarzony ładunkiem

W wodnych roztworach, kwasy i zasady obdarzone ładunkiem są całkowicie zdysocjowane i wchodzą w reakcje protolityczne z wodą:

np.:

H₂O + HCOO^-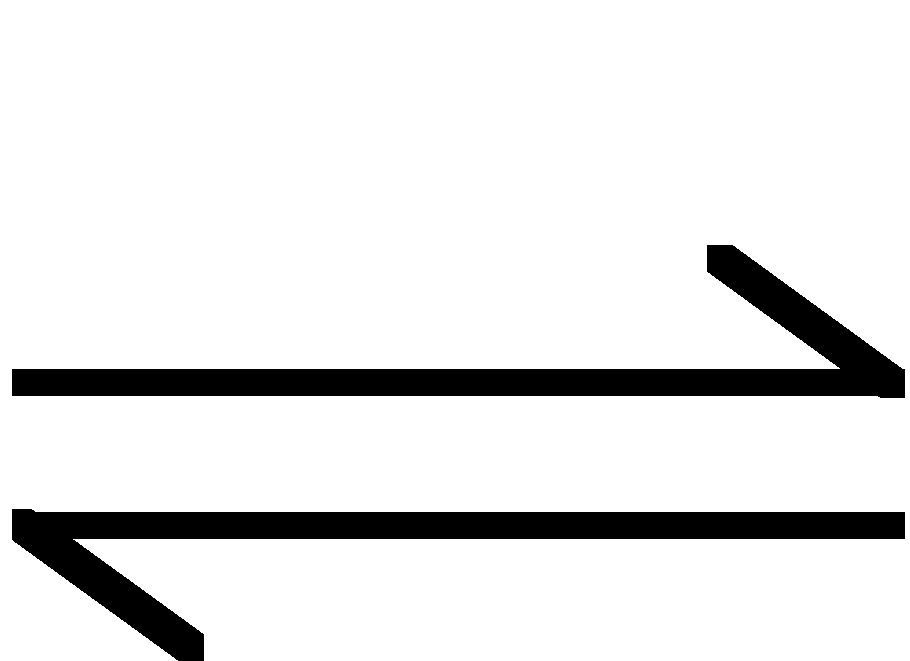
HCOOH + OH^-

  kwas 1 zasada 2 kwas 2   zasada 1

+ H₂O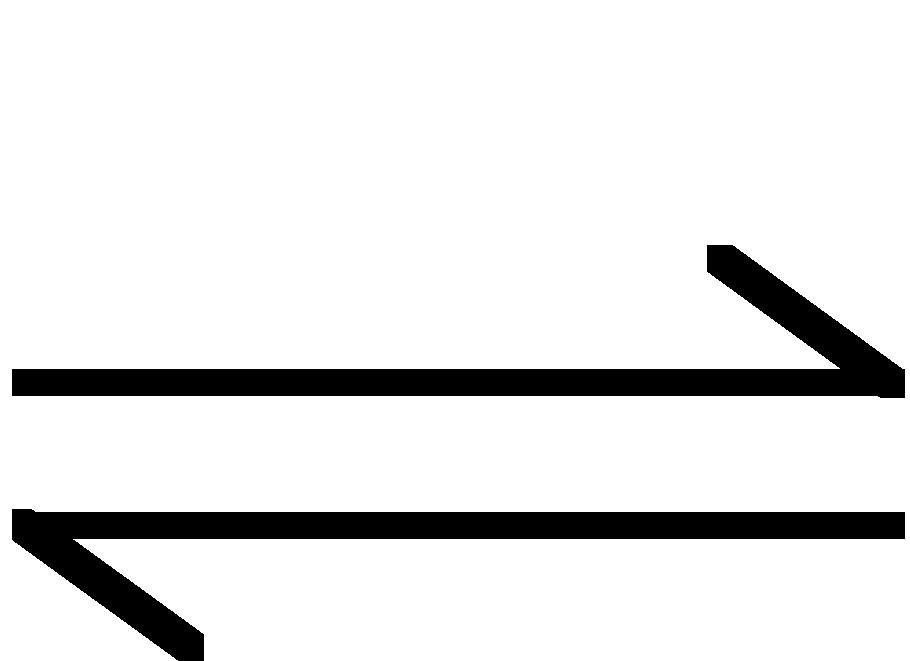

+ NH₃

  kwas 1 zasada 2 kwas 2   zasada 1

Ogólnie, stała równowagi reakcji kwas - zasada ma postać:

Przypadki szczególne:

Hydroliza anionowa:

A^- + H₂O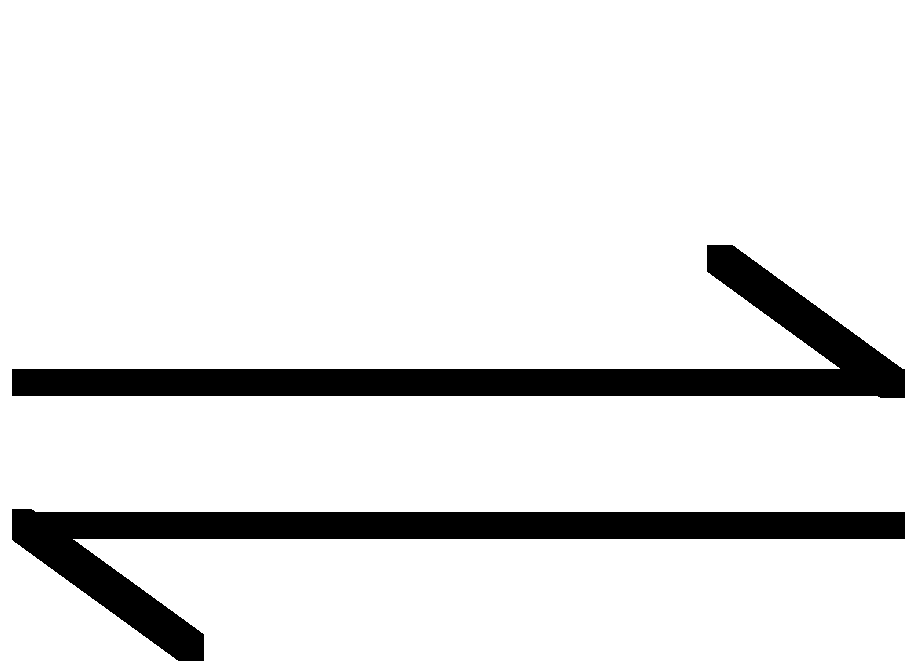
HA + OH^-

- stała równowagi tej reakcji (stała hydrolizy):

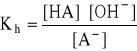
- mnożąc licznik i mianownik przez [H₃O⁺]:

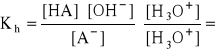
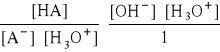
- czyli:

Stała hydrolizy anionowej jest równa stosunkowi iloczynu jonowego wody do stałej dysocjacji kwasowej, kwasu sprzężonego z zasadą obdarzoną ładunkiem.

Hydroliza kationowa:

B+ + 2 H₂O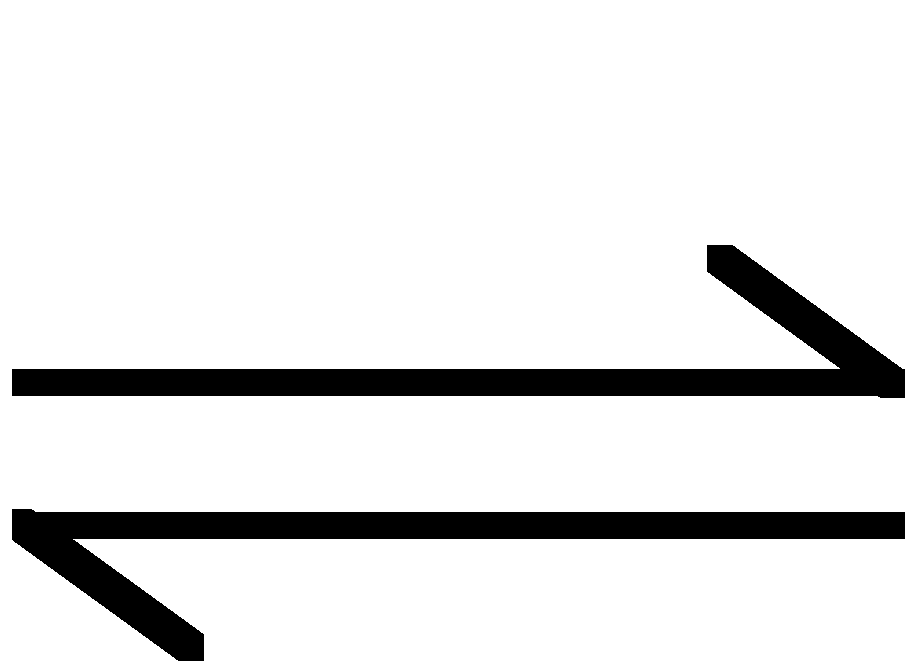
H₃O⁺ + BOH

- stała hydrolizy (stała równowagi tej reakcji):

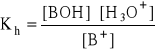
- mnożąc licznik i mianownik przez wartość [OH-]:

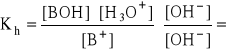
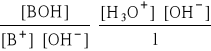
- czyli:

Stała hydrolizy kationowej jest równa stosunkowi iloczynu jonowego wody do stałej dysocjacji zasadowej, zasady sprzężonej z kwasem obdarzonym ładunkiem.

Równoczesna hydroliza anionowa i kationowa:

A^- + B+ + H₂O
HA + BOH

- stała hydrolizy:

- mnożąc licznik i mianownik przez wartość iloczynu: [H₃O⁺]*[OH-]:

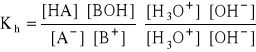
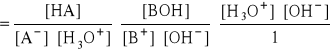
- czyli:

Konsekwencja - wartości stałych hydrolizy wynikają z wartości stałych dysocjacji odpowiednich słabych kwasów lub zasad obdarzonych ładunkiem, w tablicach chemicznych nie podaje się wartości stałych hydrolizy poszczególnych soli.

Stopień hydrolizy - β

Zależność między stopniem hydrolizy a stałą hydrolizy:

- hydroliza anionowa:

A^- + H₂O
HA + OH^-

(C_s - x)  x   x

x = β⋅C_s

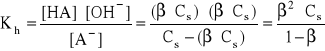
- gdy β << 1 ⇒ 1 - β ≅ 1

K_h = β²⋅C_s

- skąd:

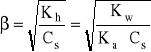
- analogicznie, w przypadku hydrolizy kationowej:

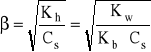
czyli:

- w przypadku hydrolizy anionowej lub kationowej, stopień hydrolizy jest odwrotnie proporcjonalny do stężenia kwasu lub zasady obdarzonej ładunkiem (hydrolizującej soli), tzn. rośnie wraz z rozcieńczaniem roztworu.

W przypadku równoczesnej hydrolizy anionowej i kationowej:

A^- + B+ + H2O
HA + BOH

(C_s - x) (C_s - x)   x  x

x = β⋅C_s

- stała hydrolizy:

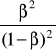
- stąd:

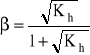
- gdy:

K_h << 1

- wyrażenie można uprościć do postaci:

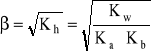
- z obu tych zależności wynika:

w przypadku równoczesnej hydrolizy anionowej i kationowej (sól słabego kwasu i słabej zasady) stopień hydrolizy nie zależy od stężenia początkowego soli.

Obliczanie wartości pH roztworów hydrolizujących soli

Hydroliza anionowa:

A^- + H₂O
HA + OH^-

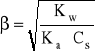
- uwzględniając:

[OH^-] = β⋅C_s i [H₃O⁺]*[OH-] = K_w

- otrzymuje się:

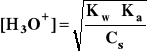
- gdzie: K_a - stała dysocjacji kwasowej kwasu HA, sprzężonego z zasadą A^-

C_s - stężenie soli = stężenie zasady A^-

Hydroliza kationowa:

B+*+ 2 H₂O
H₃O⁺ + BOH

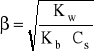
- uwzględniając:

[H₃O⁺] = β⋅C_s i [H₃O⁺]*[OH^-] = K_w

- otrzymuje się:

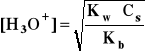
- gdzie: K_b - stała dysocjacji zasadowej zasady BOH sprzężonej z kwasem B+

C_s - stężenie soli = stężenie kwasu B+

Równoczesna hydroliza anionowa i kationowa:

A^- + B+ + H2O
HA + BOH

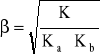
- uwzględniając:

[HA] ≅ [BOH] = β⋅C_s i [H₃O⁺]*[OH^-] = K_w

- oraz dokonując odpowiednich przekształceń otrzymuje się:

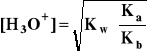
- gdzie: K_a - stała dysocjacji kwasowej kwasu HA

K_b - stała dysocjacji zasadowej zasady BOH

Przykład 2. Obliczyć stopień hydrolizy oraz pH w 0,1 molowym roztworze KCN.

K_HCN = 7,2*10^-10

- równanie dysocjacji: KCN → K+ + CN^-

- równanie hydrolizy: CN^- + H₂O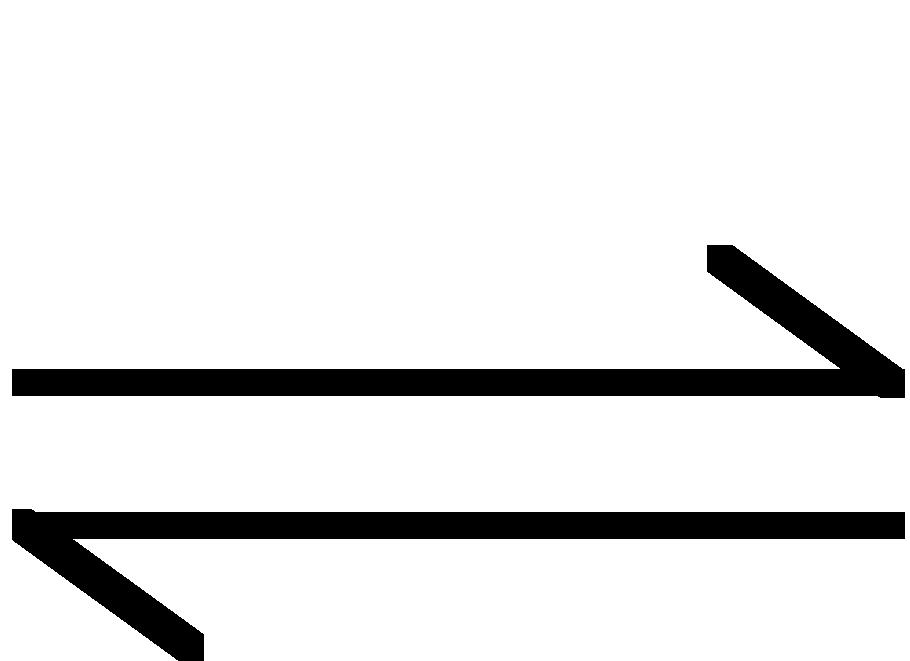
HCN + OH^-

- stopień hydrolizy anionowej:

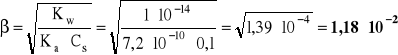
- dwa sposoby obliczania [H₃O⁺] i następnie pH:

- korzystając z gotowego wzoru:

pH = -log [H₃O⁺] = 12 - log 8,5 = 12 - 0,93 = 11,07

- korzystając z zależności:

[OH^-] = β⋅C_s = 1,18⋅10^-2⋅10^-1 = 1,18⋅10^-3

pOH = -log 1,18⋅10^-3 = 3 - log 1,18 = 3 - 0,07 = 2,93

pH = 14 - pOH = 14 - 2,93 = 11,07

Przykład 3. Obliczyć stopień hydrolizy i pH w 0,05 molowym roztworze NH₄Cl.

- równanie dysocjacji:

- równanie hydrolizy:
+ H₂O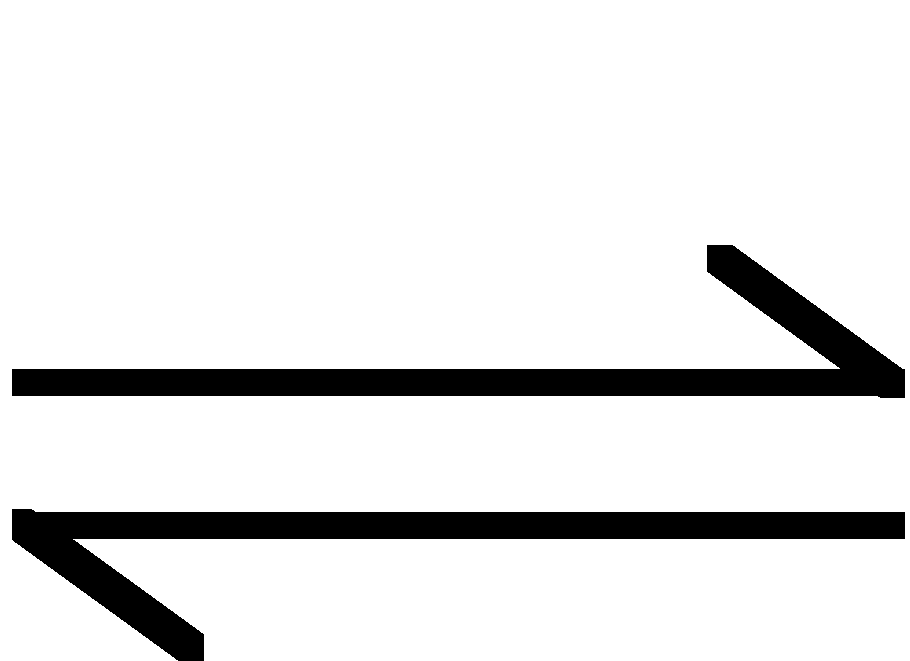

+ NH3

- stopień hydrolizy kationowej:

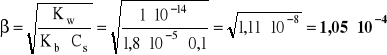
- podobnie jak poprzednio - dwa sposoby obliczania [H₃O⁺] i następnie pH:

- korzystając z gotowego wzoru:

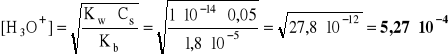
pH = -log 5,27⋅10^-6 = 6 - log 5,27 = 6 - 0,722 = 5,278

- lub z zależności:

[H₃O⁺] = β⋅C_s = 1,05⋅10^-4⋅5⋅10^-2 = 5,25⋅10^-6

pH = -log 5,25⋅10^-6 = 6 - log 5,25 = 6 - 0,720 = 5,28

Przykład 4. Obliczyć stopień hydrolizy i pH w 0,1 molowym roztworze NH4CN.

KHCN = 7,2*10^-10

- równanie dysocjacji:

- równanie hydrolizy:

- stała hydrolizy:

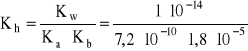
= 0,7716

- ponieważ K_b nie jest znacznie mniejsze od 1, stopień równoczesnej hydrolizy kationowej i anionowej należy obliczyć wg zależności:

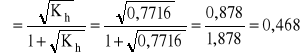
- a stężenie jonów oksoniowych, wg wyprowadzonej zależności:

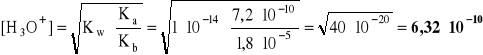
pH = -log 6,32*10^-10 = 10 - log 6,32 = 10 - 0,8 = 9,2

Zadania

1. Napisać równania reakcji hydrolizy, zachodzących w wodnych roztworach:

a) azotanu(V) żelaza(III)

b) siarczku potasu

c) chlorku miedzi(II)

d) azotanu(III) wapnia

e) siarczanu(IV) baru

f) chlorku chromu(III)

g) chloranu(I) baru

h) siarczanu(VI) cynku

i) azotanu(V) niklu

j) chloranu(III) strontu

k) bromku miedzi(II)

l) siarczku baru

Określić odczyn wodnego roztworu każdej soli.

2. W naczyniu miarowym umieszczono 1,489 g chloranu(I) sodu i dodano wodę, tak aby objętość roztworu była równa 500 cm³. Obliczyć stałą hydrolizy, stopień hydrolizy chloranu(I) sodu w powstałym roztworze i pH w powstałym roztworze.

M_Na = 23 u; M_Cl = 35,45 u; M_O = 16 u

K_{kwasu chlorowego(I)} = 4,310^-8

3. Do kolby miarowej wprowadzono 0,25 mola mrówczanu potasu i dopełniono wodą do objętości 750 cm³. Obliczyć stałą hydrolizy, stopień hydrolizy mrówczanu potasu i pH w powstałym roztworze.

K_{kwasu mrówkowego} = 1,810^-4

4. Obliczyć stałą hydrolizy, stopień hydrolizy i pH w 2 % roztworze azotanu(V) srebra. Gęstość roztworu = 1g/cm³.

M_Ag = 107 u; M_N = 14 u; M_O = 16 u

K_{wodorotlenku srebra} = 110^-4

5. W 200 cm³ roztworu zawarte jest 1,3 g cyjanku potasu. Obliczyć stałą hydrolizy, stopień hydrolizy cyjanku potasu i pH w tym roztworze.

M_K = 39 u; M_C = 12 u; M_N = 14 u

K_{kwasu cyjanowodorowego} = 810^-10

6. W 250 cm³ roztworu zawarte jest 3,96 g jodanu(V) sodu. Obliczyć stałą hydrolizy i stopień hydrolizy jodanu(V) sodu oraz pH w tym roztworze.

M_Na = 23 u; M_I = 127 u; M_O = 16 u

K_{kwasu jodowego(V)} = 2,310^-2

7. W 1 dm³ roztworu zawarte jest 2,6725 g chlorku amonu. Obliczyć stałą hydrolizy i stopień hydrolizy chlorku amonu oraz pH w tym roztworze.

M_N = 14 u; M_H = 1 u; M_Cl = 35,45 u

K_amoniaku = 1,8·10^-5

8. Obliczyć stałą hydrolizy, stopień hydrolizy i pH w 0,025 molowym roztworze cyjanku amonu.

K_amoniaku = 1,8·10^-5, K_{kwasu cyjanowodorowego} = 810^-10

Rozwiązania

2. K_h = 2,32·10^-7; β = 5,8·10^-6; pH = 7,34

3. K_h = 5,6·10^-11; β = 1,3·10^-5; pH = 8,63

4. K_h = 1,0·10^-10; β = 2,9·10^-5; pH = 5,46

5. K_h = 3,5·10^-3; β = 0,19; pH = 11,58

6. K_h = 4,3·10^-13; β = 2,4·10^-6; pH = 7,26

7. K_h = 5,5·10^-10; β = 1,05·10^-4; pH = 3,98

8. K_h = 0,7; β = 0,83; pH = 9,18

Ka	Kwas	Zasada	Kb
4,45*10^-^7	H2CO3		2,25*10^-^8
4,7*10^-^11			2,13*10^-^4
1,8*10^-^4	HCOOH		5,6*10^-^11
4,0*10^-^4	HNO2		2,5*10^-^11
1,8*10^-^5	CH3COOH		5,5*10^-^10
1,2*10^-^2			8,33*10^-^12
1,0*10^-^7	H2S		1,0*10^-^7
1,0*10^-^13			1,0*10^-^1
5,5*10^-^10		NH3	1,8*10^-^5
4,0*10^-^10	HCN		2,5*10^-^5
1,70*10^-^1	HIO3		5,9*10^-^14
7,7*10^-^11	Cu^2+	Cu(OH)2	1,3*10^-^4
7,7*10^-^11	Fe^2+	Fe(OH)2	1,3*10^-^4
2,5*10^-^10	Zn^2+	Zn(OH)2	4*10^-^5
4*10^-^12	Mg^2+	Mg(OH)2	2,5*10^-^3
2*10^-^2	H2SO3		5*10^-^13
1,02*10^-^7			9,0*10^-^8

9

liczba cząstek zhydrolizowanych

początkowa liczba cząstek

---