gdzie
oznacza moment bezwładności pola przekroju ciała płaszczyzną pływania względem osi x (obliczony zgodnie z oznaczeniami osi przyjętymi na rys. 2.8c). Wprowadzając tę zależność do wzoru (2.38) obliczamy

(2.40)

gdzie τ jest objętością zanurzonej części ciała.

Oznaczmy odległość środka ciężkości od środka wyporu literą a; przyj-miemy
gdy środek ciężkości leży powyżej środka wyporu. Przedłużając linię działania siły
otrzymujemy na przecięciu się z osią punkt M, nazywany punktem metacentrycznym lub metacentrum . Odległość metacentrum od środka ciężkości nazywa się wysokością metacentryczną; jest ona oznaczana literą m. Przyjmuje się w przypadku gdy metacentrum leży powyżej środka ciężkości
Z rys. 2.8b i 2.8d wynika, że ciało pływające na powierzchni jest stateczne w zakresie małych wychyleń z położenia równowagi o elementarnie mały kąt, gdy odległość metacentryczna jest dodatnia

(2.41)

Z zależności geometrycznych, widocznych na rys. 2.8b, wyznaczamy

i następnie po wykorzystaniu (2.40) ostatecznie otrzymujemy

(2.42)

ĆWICZENIA

Przykład 2.1. Mikromanometr napełniony dwiema cieczami nie mieszającymi się o różnych gęstościach i zbudowano w kształcie U-rurki z dwoma zbiorniczkami (rys. 2.9). Średnica rurki d = 8 mm, średnica zbiorniczka D = 80 mm. Określić zależność pomiędzy różnicą ciśnień
a wysokością h słupa cięższej cieczy.

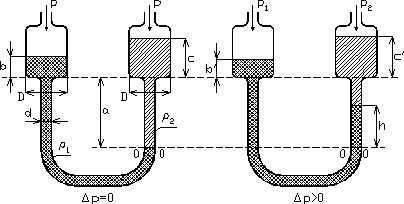
Rys. 2.9

Z rys. 2.9 wynikają zależności:

które odejmujemy stronami

Z porównania wypartych objętości cieczy mamy

oraz

czyli

Po wykorzystaniu tych wzorów uzyskujemy związek

i ostatecznie otrzymujemy

Przykład 2.2. Do U-rurki zatopionej z jednej strony nalewano stopniowo rtęci (rys. 2.10). Znając ciśnienie atmosferyczne oraz wysokość rurki h, wyprowadzić zależność między wysokościami a i b poziomów rtęci w obu ramionach U-rurki.

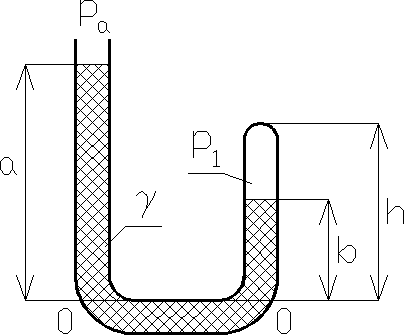
Rys. 2.10

Zakładamy, że sprężanie powietrza w zamkniętym ramieniu U-rurki odbywa się izotermicznie. Obowiązuje więc w tym przypadku prawo Boyle'a-Mariotte'a

gdzie jest nieznanym ciśnieniem powietrza.

Drugie równanie wynika z warunku równości ciśnień na poziomie 0-0:

Po wyeliminowaniu ciśnienia
otrzymujemy:

Przykład 2.3. W akumulatorze hydraulicznym (rys. 2.11) całkowicie wypełnionym olejem o gęstości
zainstalowano dwa cylindry z tłokami, przesunięte względem siebie o wysokość h = 0,5 m. Na tłok o średnicy d = 25 mm działa siła
Jaką siłę należy przyłożyć do drugiego tłoka, o średnicy D = 100 mm, aby układ znajdował się w stanie równowagi?

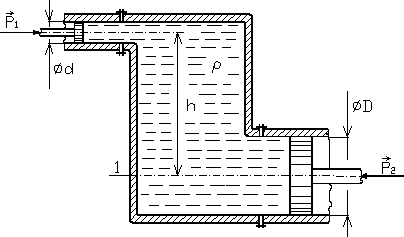
Rys. 2.11

Ciśnienie na poziomie osi symetrii tłoka o średnicy D (poziom 1 na rys. 2.11) wynosi

.

Ponieważ:

zatem

Z ostatniej zależności wyznaczamy siłę

Po podstawieniu danych liczbowych otrzymamy

Przykład 2.4. Cylindryczny zbiornik wypełniony cieczą wiruje dookoła pionowej osi ze stałą prędkością kątową ω (rys. 2.12a). Wyznaczyć kształt powierzchni swobodnej w zbiorniku oraz określić rozkład ciśnienia.

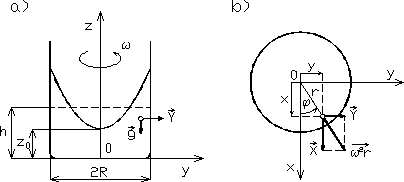
Rys. 2.12

Jednostkowa siła masowa działająca na dowolną cząstkę w naczyniu (rys. 2.12b) jest wypadkową jednostkowej siły ciężkości i jednostkowej siły bezwładności, które wyrażają się następującymi zależnościami:

Równanie powierzchni ekwipotencjalnej ma postać

po jego scałkowaniu uzyskujemy związek

który łatwo można zapisać w układzie współrzędnych cylindrycznych

Powierzchnie ekwipotencjalne (również powierzchnia swobodna) są więc paraboloidami obrotowymi.

Z warunku dla mamy

a stałą można wyznaczyć porównując objętość cieczy w spoczynku i ustalonym ruchu obrotowym.

Rozkład ciśnienia wynika z rozwiązania równania (2.9). Po jego scałkowaniu i wyznaczeniu stałej całkowania z warunku dla , otrzymujemy

Przykład 2.5. Określić stosunek wysokości zapory do jej szerokości z warunku, że moment Ph wywracający zaporę stanowi połowę momentu ustateczniającego G b (rys. 2.13). Długość zapory w kierunku normalnym do płaszczyzny przedstawionej na rysunku 2.13 wynosi L; zaporę traktujemy jako bryłę jednorodną o ciężarze właściwym ; ciężar właściwy wody .

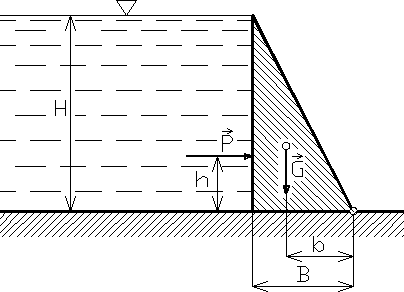
Rys. 2.13

Parcie działające na zaporę obliczamy ze wzoru (2.26)

Odległość punktu przyłożenia wypadkowej parcia od zwierciadła wody jest określona wzorem (2.28). Wobec tego

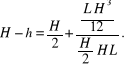
Zważywszy następnie, że:

ze wzoru

obliczamy

Przykład 2.6. Zbiornik wody jest zamknięty obrotową płytą, wygiętą w kształcie ćwiartki walca kołowego i obracającą się względem osi, której śladem jest punkt S (rys. 2.14). Należy obliczyć wypadkowe parcie
na płytę, jego punkt przyłożenia oraz moment względem osi S. Szerokość zbiornika wynosi L.

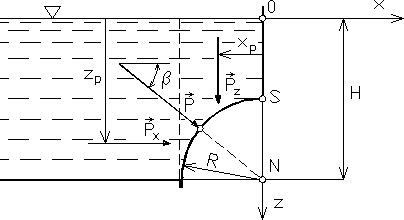
Rys. 2.14

Składowe Px i Pz wynikają bezpośrednio ze wzorów (2.30) i wynoszą:

Dowolne parcie elementarne przechodzi przez punkt N, przez ten punkt będzie również przechodzić wypadkowa układu parć elementarnych. Stąd wyznaczymy
kąt β, jaki tworzy siła
z płaszczyzną poziomą.

Linia działania składowej Px jest określona wzorem (2.31); jej odległość od zwierciadła cieczy jest więc równa

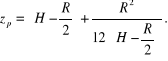
Linia działania składowej Pz przechodzi przez środek ciężkości bryły jednorodnej, o podstawie będącej różnicą powierzchni H R i ćwiartki koła; jej położenie określamy wykorzystując wzór (2.32)

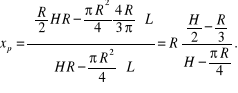
Moment MS wypadkowej
względem osi S jest sumą momentów obu składowych Px i Pz względem tej osi

Przykład 2.7. Areometr zanurza się w wodzie o gęstości
do głębokości
a w cieczy o gęstości
do głębokości
Na jaką głębokość
zanurzy się on w cieczy o gęstości

Na podstawie prawa Archimedesa możemy napisać następujące równania równowagi

gdzie
oznacza masę areometru,
- przekrój rurki areometru, a
- objętość ku-listej części areometru.

Z powyższych równań otrzymamy

skąd wynikają dwie zależności dla przekroju rurki areometru:

z których wyznaczamy szukaną wielkość

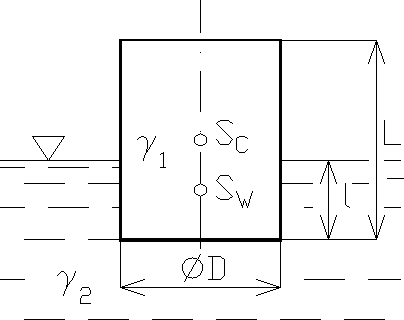
Przykład 2.8. Obliczyć stosunek średnicy D do tworzącej L walca kołowego jednorodnego o ciężarze właściwym
pływającego w cieczy o ciężarze właściwym
w taki sposób, że jego tworzące są normalne do zwierciadła cieczy (rys. 2.15).

Rys. 2.15

Warunek równowagi trwałej wynika ze wzorów (2.41) i (2.42). Obliczamy poszczególne wielkości. Moment bezwładności płaszczyzny pływania względem osi poziomej x wynosi

Objętość zanurzona

Odległość środka ciężkości SC od środka wyporu SW

Po podstawieniu tych wielkości do warunku (2.42) otrzymujemy

46

---