I Wstęp teoretyczny

Za pomocą maszyny Atwooda możemy wyznaczyć przyspieszenie ruchomych bloczków. Wyznaczamy je z czasu t , jaki potrzebny jest do przebycia stałej drogi S. Korzystamy ze wzoru na przyspieszenie ciała, którego prędkość początkowa równa jest zero :

Dzięki obliczonemu przyspieszeniu jesteśmy w stanie podać moment bezwładności bloczka K :
, gdzie : k- liczba ciężarków ;m- masa ciężarka; g- przyspieszenie ziemskie ;a- przyspieszenie ciężarka ;M-masa bloczka zawieszonego na nici; r- promień bloczka K.Kiedy dołączymy na osi bloczka K pierścień i ponownie obliczymy moment bezwładności to z różnicy z obu momentów bezwładności, otrzymamy moment bezwładności pierścienia, który jest celem ćwiczenia.

II Opracowanie ćwiczenia

1) Obliczenie średniej drogi spadku

l.p.	s [m]	[m]
1	0,860
2	0,862
3	0,863
4	0,862
5	0,861	0,862
6	0,862
7	0,861
8	0,864
9	0,863
10	0,862

2) Dla obu serii pomiarowych obliczamy średni czas spadku
, a następnie przyspieszenie

;
;

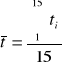
l.p.	[s]	[s]	[s]	[s]	[m/s2]	[m/s2]
1	2,653	4,549
2	2,667	4,316
3	2,689	4,299
4	2,709	4,328
5	2,700	4,433
6	2,725	4,168
7	2,768	4,110	2,67	4,30	0,242	0,093
8	2,630	4,059
9	2,653	4,326
10	2,628	4,473
11	2,629	4,134
12	2,626	4,157
13	2,647	4,302
14	2,631	4,540
15	2,646	4,331

3) Na podstawie wzoru z części teoretycznej wyznaczamy moment bezwładności J
(bez pierścienia) i J
(z pierścieniem) :

l.p.	[kg*m ]	[kg*m ]
1	0,0009	0,0105

4) Moment bezwładności pierścienia wynosi J
= J
-J
=0,0105-0,0009=0,0095 [kg*m
]

5) odchylenie standardowe S:

l.p.	s [m]	[m]	s- [m]	(s- ) [m ]	[m]
1	0,860		-0,002	4E-06
2	0,862		0,000	0
3	0,863		0,001	1E-06
4	0,862		0,000	0
5	0,861	0,862	-0,001	1E-06	0,0004
6	0,862		0,000	0
7	0,861		-0,001	1E-06
8	0,864		0,002	4E-06
9	0,863		0,001	1E-06
10	0,862		0,000	0
				suma
				0,000012

Odchylenie standardowe t
i t
:

l.p.	t [s]	[s]	t - [s]	(t - ) [s ]	[s]
1	2,653		-0,014	0,0002
2	2,667		0,000	0,0000
3	2,689		0,022	0,0005
4	2,709		0,042	0,0018
5	2,700		0,033	0,0011
6	2,725		0,058	0,0034
7	2,768	2,67	0,101	0,0103	0,0110
8	2,630		-0,037	0,0013
9	2,653		-0,014	0,0002
10	2,628		-0,039	0,0015
11	2,629		-0,038	0,0014
12	2,626		-0,041	0,0017
13	2,647		-0,020	0,0004
14	2,631		-0,036	0,0013
15	2,646		-0,021	0,0004
				suma:
				0,0254

l.p.	t [s]	[s]	t - [s]	(t - ) [s ]	[s]
1	4,549		0,247	0,061
2	4,316		0,014	0,000
3	4,299		-0,003	0,000
4	4,328		0,026	0,001
5	4,433		0,131	0,017
6	4,168		-0,134	0,018
7	4,110	4,30	-0,192	0,037	0,039
8	4,059		-0,243	0,059
9	4,326		0,024	0,001
10	4,473		0,171	0,029
11	4,134		-0,168	0,028
12	4,157		-0,145	0,021
13	4,302		0,000	0,000
14	4,540		0,238	0,057
15	4,331		0,029	0,001
				suma:
				0,329

6. Średni błąd kwadratowy

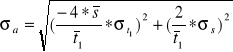
Średni błąd kwadratowy J
:

J
=-0,00033[kg*m

J
=
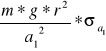
=-0,00005 [kg*m

J

7. Teoretyczny moment bezwładności obliczamy ze wzoru : J=
=0,5*2,001*(0,05*0,05+0,82*0,82)=0,0092 [kg*m

Moment bezwładności obliczony za pomocą maszyny Atwooda wynosi

0,0095
, a teoretyczny moment bezwładności wynosi 0,0092 [kg*m
. Po uwzględnieniu błędu przypadkowego , możemy stwierdzić , że obliczony moment bezwładności jest porównywalny z błędem teoretycznym. Cel ćwiczenia został osiągnięty, świadczy to o tym, iż maszyna Atwooda , może być wykorzystywana do doświadczeń w wyznaczaniu momentów bezwładności brył sztywnych.

---