Wstęp teoretyczny

Ciałem sztywnym nazywamy ciało, którego wszystkie punkty mają stałe położenie względem siebie

Elipsoida bezwładności to powierzchnia utworzona przez końce odcinków r_x , r_y , r_z odłożonych na wszystkich osiach przechodzących przez środek masy ciała.

Odcinki odłożone na głównych osiach bezwładności są odpowiednio równe:

;
;

gdzie: I_xx, I_yy, I_zz - momenty bezwładności względem osi x, y, z.

Moment bezwładności jest to suma iloczynów mas przez kwadraty odległości od osi obrotu przechodzącej przez środek masy

Przebieg ćwiczenia

1. Pomiar wymiarów obciążników w postaci sześcianu, prostopadłościanu o podstawie prostokąta, prostopadłościanu o podstawie kwadratu. Każdy pomiar wykonujemy pięciokrotnie.

2. Pomiar czasu 10 wahnięć wahadła nieobciążonego.

3. Pomiar czasu 10 wahnięć wahadła po zamocowaniu w ramce obciążnika w postaci sześcianu.

4. Pomiar czasu 10 wahnięć wahadła po zamocowaniu w ramce obciążnika w postaci prostopadłościanu dla trzech głównych osi bezwładności oraz dla głównej przekątnej.

5. .

pomiary wymienione w punktach 2 - 4 wykonano trzykrotnie

Opracowanie wyników.

1. Wymiary obciążników

	sześcian	Prostopadłościan 1
lp.	a [cm]	a [cm]	b [cm]	c[m]
1.	50,2	50,2	50,0	100,1
2.	50,1	50,0	50,1	100,2
3.	50,2	50,0	50,0	100,2
4.	50,0	50,1	50,2	100,2
5.	50,2	50,1	50,1	100,1
średnia	50,14	50,08	50,08	100,16
odchylenie	0,089	0,084	0,084	0,055

aa= 0,5014 ±0,0089[m]

a=0,5008 ±0,0084 [m]

b=0,5008±0,0084 [m]

c=1,0016±0,0055 [m]

Masa sześcianu M_s = 980 g = 0,98 [kg]

Masa prostopadłościanu 1 M₁ = 1884 [g] = 1,884 [kg]

. Czasy 10 wahnięć wahadła skrętnego [s]

10T	t[s]
		1	2	3	średnia	odchylenie
Wahadło nieobciążone	7,994	7,998	7,998	7,997	0,0023
Obciążone sześcianem	10,040	10,059	9,987	10,029	0,0373
I główna oś a prostopadłościanu	11,624	11,622	11,628	11,625	0,0031
II główna oś b prostopadłościanu	11,669	11,644	11,677	11,663	0,0172
III główna przekątna oś c prostopadłościanu	15,805	15,809	15,814	15,809	0,0045
Wzdłuż głównej przekątnej prostopadłościanu	13,245	13,256	13,248	13,250	0,0057

gdzie: średnia
odchylenie standardowe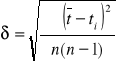

Obliczenie okresów drgań wahadła

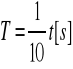
Okres 1 drgania wahadła nieobciążonego

T_o = (0,7997+/-0,0023) [s]

Okres 1 drgania wahadła obciążonego sześcianem)

T_s = (1,0029+/-0,0037) [s]

Okres 1 drgania wahadła obciążonego prostopadłościanem 1 względem I głównej osi bezwładności (a)

T_I = (1,16250+/-0,00031) [s]

Okres 1 drgania wahadła obciążonego prostopadłościanem 1 względem II głównej osi bezwładności (b)

T_II = (1,1660+/-0,0017) [s]

Okres 1 drgania wahadła obciążonego prostopadłościanem 1 względem III głównej osi bezwładności (c)

T_III = (1,5809+/-0,00045) [s]

Okres 1 drgania wahadła obciążonego prostopadłościanem 1 względem przekątnej

T_p = (1,25000+/-0,00057) [s]

Obliczanie wartość głównych momentów bezwładności dla badanego obciążnika

ze wzoru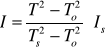

Okres wahania nieobciążonego wahadła

obciążonego sześcianem o M_s = 0,98 [kg]

obciążonego prostopadłościanem względem jednej z głównych osi bezwładności

Moment bezwładności sześcianu obliczamy ze wzoru :

gdzie a = 0,05014 [m] = 50,04•10^-3 [m] ; M_s = 980 [g] = 0.98 [kg]

a= 0,050±0,001 [m]

M= 0,980 ±0,001[kg]

[kg·m²]

[kg·m²]

I_s=(0,40900+/-0,00035)
[kg·m²]

Odtąd liczyc

Korzystając ze wzoru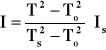
wyznaczymy moment bezwładności względem I głównej osi bezwładności (patrz. Tablica 2)

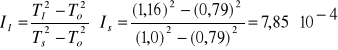
[kg·m²]

Moment bezwładności względem II głównej osi bezwładności (patrz. Tablica 2)

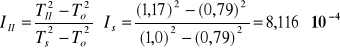
[kg·m²]

Moment bezwładności względem III głównej osi bezwładności (patrz. Tablica 2)

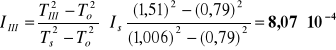
[kg·m²]

Moment bezwładności względem przekątnej prostopadłościanu (patrz. Tablica 2)

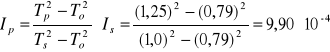
[kg·m²

Wyznaczamy równanie prostej zawierającej główną przekątną:

Współrzędne wierzchołka prostopadłościanu 1 :

W (x_w; y_w; z_w)

;
;

W (0,025; 0,025; 0,05)

Równanie przekątnej na postać :

Wyznaczamy elipsoidę bezwładności prostopadłościanu 1 o podstawie prostokąta :

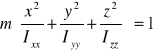
lub równanie elipsoidy

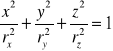
wiemy że I_xx = I_I, I_yy = I_II oraz że I_zz =I_III

więc

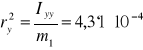
Rozwiązujemy układ równań i wyznaczamy punkty przebicia prostej zawierającej przekątną główną z elipsoidą bezwładności :

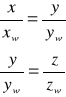
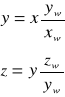
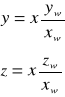
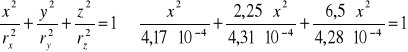
⋅10^-2 [m]

10^-2 [m]

10^-2 [m]

Równanie elipsoidy bezwładności ma postać :

Obliczamy moment bezwładności względem przekątnej głównej prostopadłościanu 1 wynosi :

I_p = 9,90⋅10^-4[kg·m²]

Ten sam moment można obliczyć ze wzoru :

=m((0,7)²+(1)²+(1,5)²)=2,94*10^-4

I_ap = 2,94·10^-4 [kg·m²]

I_a = I_ap

[kg·m²]

Schematyczne obliczenie pochodnej momentu I_x względem T_x, T_o, T_s

I_s = 4,08·10^-4 [kg·m²] T_s = 1,000+/-0,001[s]

I_I = 7,85·10^-4 [kg·m²] T_I = 1,160 +/-0,001 [s]

I_II = 8,12·10^-4[kg·m²] T_II = 1,169+/-0,001 [s]

I_p = 9,90·10^-4 [kg·m²] T_p = 1,249+/-0,001 [s]

T_o = 0,799+/-0,001 [s]

[s]

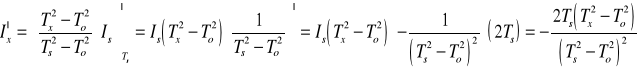
Niepewności jakimi obarczone są wyznaczone wartości momentów bezwładności ciała :

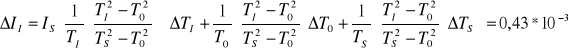
[kg m²]

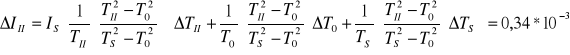
[kg m²]

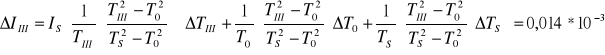
[kg m²]

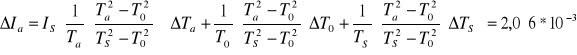
[kg m²]

Zestawienie wyników :

- pomiary obciążników i czasy wahnięć podane w tabelach

- moment bezwładności względem I głównej osi bezwładności

I_I = (7,85±0.043)·10^-4 [kg·m²]

- moment bezwładności względem II głównej osi bezwładności

I_II = (8,12±0,034)·10^-4 [kg·m²]

- moment bezwładności względem III głównej osi bezwładności

I_III = (80,71±0,01)·10^-3 [kg·m²]

Wnioski

• Celem ćwiczenia było wyznaczenie głównych momentów bezwładności sześcianu i prostopadłościanu

• Wyniki uzyskane w czasie pomiarów , a także przy obliczeniach są obciążone błędem obserwatora i zaokrąglenia liczb

• Przy porównaniu dwóch wyników momentu bezwładności względem głównej przekątnej wystąpiła różnica wynikająca z niedokładności pomiaru

Politechnika Śląska w Katowicach

SPRAWOZDANIE

Temat: Wyznaczanie elipsoidy bezwładności ciała sztywnego.

Grupa ZIP21

Sekcja 10:

Bartczak Tomasz Straszak Bartosz

---