Opis rozkładu zmiennych powstał na podstawie matryc dostępnych w załącznikach na końcu dokumentu.
Teksty kursywą napisane są wyłącznie dla lepszego zrozumienia treści- NIE PRZEPISYWAĆ
Pogrubione zostały najważniejsze fragmenty.
Kierunek aspiracji edukacyjnych. (zmienna jakościowa)
Wypisanie wszystkich wartości zmiennej występujących w danej zbiorowości (zliczamy wszystkie 1 po kolei dla każdej wartości zmiennej oddzielnie; wartość zmiennej to np. Społ., Ling., Techn.).
Społeczny - 34
Lingwistyczny - 8
Techniczny - 11
Medyczny - 16
Ekonomiczny - 12
Informatyczny - 4
Inny - 14
Brak danych - 1 (tam gdzie są same 0- prościej różnica między liczbą wszystkich możliwych odp. a ilością 1 )
Grupowanie- połączenie w jedną; 2 podobnych do siebie kategorii zmiennej z których wartość (ni) jednej nie przekracza 5 dla małych grup a 8 dla dużych grup >30 os. Techniczny (11) + informatyczny (4) = Techniczny/Informatyczny 15
Tab. 1. Kierunek aspiracji edukacyjnych (zmienna jakościowa - relacja różny-równy)
Dominanta- wartość dominująca, najwyższa:
Wartości zmiennej (k) to np. Społ., Ling., Techn. itd.
Wykres
Wypisanie wszystkich wartości zmiennej występujących w danej zbiorowości (zliczamy wszystkie 1 po kolei dla każdej wartości zmiennej oddzielnie; wartość zmiennej ma różne kategorie np. wys. zarobki, niezal. zawod.).
Grupowanie- połączenie w jedną; 2 podobnych do siebie kategorii zmiennej z których wartość (ni) jednej nie przekracza 5 dla małych grup a 8 dla dużych grup >30 os. Władza (8) + Popularność (2) = Władza/Popularność 10
Tab. 3.. Kierunek aspiracji zawodowych (zmienna jakościowa - relacja różny-równy)
Dominanta- wartość dominująca, najwyższa:
Wskaźnik struktury (wi)- częstość, z jaką realizuje się wskazana wartość badanej zmiennej. Dla rozkładu wyróżniamy tyle wskaźników struktury, ile rozróżniliśmy wartości zmiennej.
Wartości zmiennej (k) to np. Niezależność zadom., Władza/ Popul..
Wykres
Wypisanie wszystkich wartości zmiennej występujących w danej zbiorowości (zliczamy wszystkie 1 dla mężczyzn i 2 dla kobiet dla każdej wartości zmiennej oddzielnie; wartość zmiennej ma różne kategorie np. męcz. kob.).
Tab. 5. Płeć (zmienna jakościowa - relacja różny-równy)
Dominanta- wartość dominująca, najwyższa:
Wskaźnik struktury (wi)- częstość, z jaką realizuje się wskazana wartość badanej zmiennej. Dla rozkładu wyróżniamy tyle wskaźników struktury, ile rozróżniliśmy wartości zmiennej.
Wartości zmiennej (k) to mężczyźni i kobiety.
Wykres
Poziom aspiracji mierzony jest w skali od 1 do 6; gdzie 1 to poziom niski, natomiast poziom wysoki.
Próbkę o liczebności parzystej N=2n (100=2*n) (gdzie n to dowolna liczba naturalna) można podzielić na dwie równoliczne części; ostatni element należący do dolnej połówki jest element o randze n (czyli N/2=n) i jego będziemy przyjmować za element środkowy przy parzystej liczności próbki.
Rozkład jest jednomodalny gdyż tylko jedna wartość występuje częściej niż pozostałe.
Dominanta- wartość dominująca, najwyższa:
Wartości zmiennej (k) to poziomy od 1 do 6.
Wykres
Stosunek do szkoły mierzony jest w skali od 1 do 5; gdzie 1 to stosunek pozytywny, natomiast 5 stosunek negatywny.
Próbkę o liczebności parzystej N=2n(gdzie n to dowolna liczba naturalna) (100=2*n) można podzielić na dwie równoliczne części; ostatni element należący do dolnej połówki jest element o randze n (czyli N/2=n) i jego będziemy przyjmować za element środkowy przy parzystej liczności próbki.
Rozkład jest dwumodalny gdyż dwie wartość występuje częściej niż pozostałe.
W związku z dwumodalnością zastosowany zostanie podział dychotomiczny
Wartości zmiennej (k) to poziomy od 1 do 5.
Wykres
Osiągnięcia dydaktyczne mierzone są w 3 stopniowej skali negatywne, przeciętne i wysokie.
Próbkę o liczebności parzystej N=2n (gdzie n to dowolna liczba naturalna) (96=2*n) można podzielić na dwie równoliczne części; ostatni element należący do dolnej połówki jest element o randze n (czyli N/2=n) i jego będziemy przyjmować za element środkowy przy parzystej liczności próbki.
Rozkład jest jednomodalny gdyż tylko jedna wartość występuje częściej niż pozostałe.
Dominanta- wartość dominująca, najwyższa:
Wartości zmiennej (k) to stopnie neg., przec., wys..
Wykres
Osiągnięcia wychowawcze mierzone są w 3 stopniowej skali negatywne, bierny, aktywny.. Braki danych, czyli brak odpowiedzi poszczególnych respondentów wynoszą 4.
Próbkę o liczebności parzystej N=2n (gdzie n to dowolna liczba naturalna) (96=2*n) można podzielić na dwie równoliczne części; ostatni element należący do dolnej połówki jest element o randze n (czyli N/2=n) i jego będziemy przyjmować za element środkowy przy parzystej liczności próbki.
Rozkład jest jednomodalny gdyż tylko jedna wartość występuje częściej niż pozostałe.
Dominanta- wartość dominująca, najwyższa:
Wartości zmiennej (k) to stopnie neg., przec., wys..
Wykres
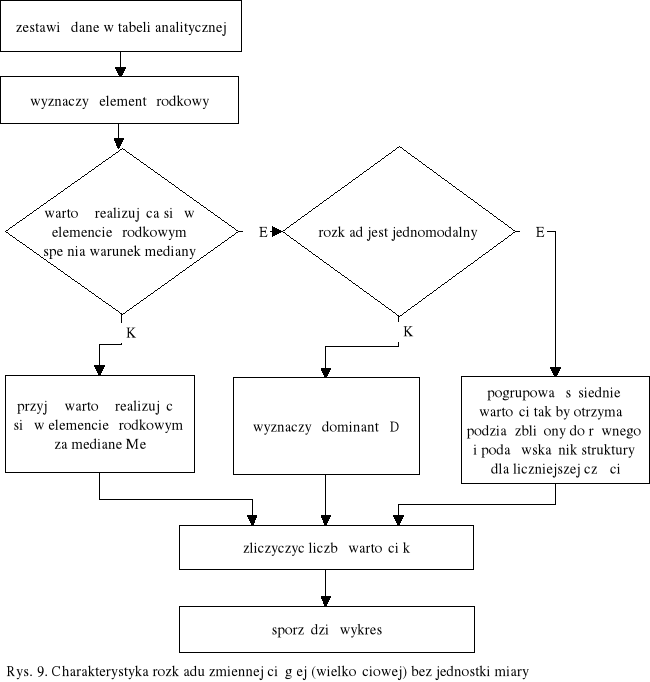
Wypisać wszystkie wartości zmiennej występujące w badanej zbiorowości. Jeśli liczba wartości k jest taka, że wartości występują średnio co najmniej pięć razy dla małych zbiorowości oraz co najmniej osiem razy dla dużych zbiorowości, to przyjmujemy ją za miarę zmienności rozkładu. Jeśli natomiast liczba wartości nie spełnia tego warunku, to dokonujemy grupowania wartości, ustalając liczbę wartości k, tak by warunek spełniała.
Dane zestawiamy w tabeli analitycznej.
Określamy dominantę D wraz z jej wskaźnikiem struktury wD.
Sporządzamy wykres.
Dane zestawiamy w tabeli analitycznej.
Wyznaczamy element środkowy.
Sprawdzamy, czy wartość realizująca się w elemencie środkowym spełnia warunek mediany.
Jeśli spełnia, to przyjmujemy ją za medianę Me.
Jeśli nie spełnia, to sprawdzamy, czy rozkład jest jednomodalny.
Jeśli jest jednomodalny, to wyznaczamy dominantę D.
Jeśli rozkład jest wielomodalny, to dokonujemy połączenia wartości sąsiednich, tak by otrzymać podział zbliżony do równego, i podajemy wskaźnik struktury dla liczniejszej części.
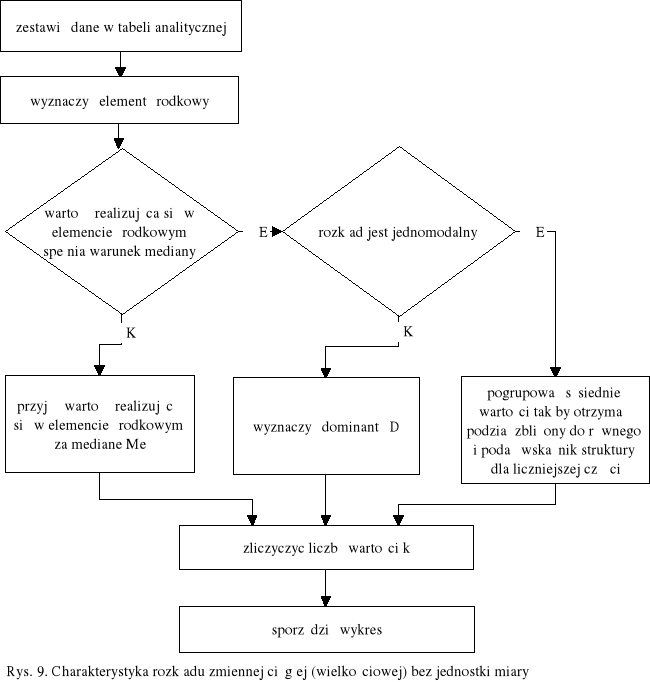
Zliczamy liczbę wartości k.Sporządzamy wykres.
Kierunek aspiracji edukacyjnych |
ni |
Społeczny |
34 |
Lingwistyczny |
8 |
Techniczny/Informatyczny |
15 |
Medyczny |
16 |
Ekonomiczny |
12 |
Inny |
14 |
Razem (N) |
99 |
Źródło: dane umowne
D= kierunek Społeczny.
Wskaźnik struktury (wi)- częstość, z jaką realizuje się wskazana wartość badanej zmiennej. Dla rozkładu wyróżniamy tyle wskaźników struktury, ile rozróżniliśmy wartości zmiennej.
wi = ( ni/N) *100%;
% = wD * 100%
wD- Wskaźnik struktury odnoszący się do dominant
wD = (D=34 podzielić na N=99)
wD = 0,34
wD = 34%
Tab. 2. Kierunek aspiracji edukacyjnych- wskaźnik struktury (zmienna jakościowa - relacja różny-równy)
Kierunek aspiracji edukacyjnych |
Liczebność ni |
Wskaźnik struktury wi |
% |
Społeczny |
34 |
0,34 |
34 |
Lingwistyczny |
8 |
0,08 |
8 |
Techniczny/informatyczny |
15 |
0,15 |
15 |
Medyczny |
16 |
0,16 |
16 |
Ekonomiczny |
12 |
0,12 |
12 |
Inny |
14 |
0,14 |
14 |
|
99 |
≈1,00 |
≈100 |
Źródło: dane umowne
≈ - to oznacza w przybliżeniu, gdyż wychodzi dopiero po dodaniu setnych i tysięcznych części ułamka
K = 6
Rys. 1. Kierunek aspiracji edukacyjnych (zmienna jakościowa - relacja różny-równy)
Źródło: dane umowne
Kierunek aspiracji zawodowych (zmienna jakościowa)
Wysokie zarobki - 55
Popularność - 2
Satysfakcja z wykonywania zawodu - 69
Władza - 8
Niezależność zawodowa - 27
Kierunek aspiracji zawodowych |
ni |
Wysokie zarobki |
55 |
Władza/ popularność |
10 |
Satysfakcja z wykonywania zawodu |
69 |
Niezależność zawodowa |
27 |
Razem (N) |
161 |
Źródło: dane umowne
D= Satysfakcja z wykonywania zawodu.
wi = ( ni/N) *100%;
% = wD * 100%
wD- Wskaźnik struktury odnoszący się do dominanty
wD = (D=69 podzielić na N=161)
wD = 0,43
wD = 43%
Tab. 4. Kierunek aspiracji zawodowych - wskaźnik struktury (zmienna jakościowa - relacja różny-równy)
Kierunek aspiracji zawodowych |
Liczebność ni |
Wskaźnik struktury wi |
% |
Wysokie zarobki |
55 |
0,34 |
34 |
Władza/ Popularność |
10 |
0,06 |
6 |
Satysfakcja z wykonywania zawodu |
69 |
0, 43 |
43 |
Niezależność zawodowa |
27 |
0,17 |
16 |
|
161 |
1,00 |
100 |
Źródło: dane umowne
k = 4
Rys. 2.. Kierunek aspiracji zawodowych (zmienna jakościowa - relacja różny-równy)
Źródło: dane umowne
Płeć (zmienna jakościowa)
Mężczyźni - 33
Kobiety - 67
Płeć |
ni |
Mężczyźni |
33 |
Kobiety |
67 |
Razem (N) |
100 |
Źródło: dane umowne
D= kobiety
wi = ( ni/N) *100%;
% = wD * 100%
wD- Wskaźnik struktury odnoszący się do dominanty
wD = (D=67 podzielić na N=100)
wD = 0,67
wD = 67%
Tab. 6. Płeć - wskaźnik struktury (zmienna jakościowa - relacja różny-równy)
Kierunek aspiracji edukacyjnych |
Liczebność ni |
Wskaźnik struktury wD |
% |
Mężczyźni |
33 |
0,33 |
33 |
Kobiety |
67 |
0,67 |
67 |
|
161 |
1,00 |
100 |
Źródło: dane umowne
k = 2
Rys. 3. Płeć (zmienna jakościowa - relacja różny-równy)
Źródło: dane umowne
Poziom aspiracji zmienna wielkościowa (ciągła) mierzonej bez jednostki miary.
Wypisanie do tabeli wszystkich wartości zmiennej występujących w danej zbiorowości (zliczamy wszystkie 1 dla poz.1 i 2 dla poz.2 itd. dla każdej wartości zmiennej oddzielnie; wartość zmiennej ma różne kategorie np. poz. 1, poz. 2, poz. 3).
Tab. 7. Poziom aspiracji (zmienna ciągła bez jednostki miary - relacja porządku)
Poziom aspiracji |
ni |
Poziom 1 |
3 |
Poziom 2 |
2 |
Poziom 3 |
6 |
Poziom 4 |
11 |
Poziom 5 |
15 |
Poziom 6 |
63 |
Razem (N) |
100 |
Źródło: dane umowne
Element środkowy znajduje się więc w 50 osobie, czyli 6 (najwyższym ) poziomie aspiracji.
W przypadku gdy k<N (liczba wartości jest mniejsza od liczby badanych), należy sprawdzić przy wyznaczaniu kwantyli, czy jest spełniony ich warunek definicyjny.
Element o randze n spełnia warunek mediany gdy. połowa elementów w badanej zbiorowości jest nie większa od niego. Przyjmujemy wtedy, że w elemencie o randze n realizuje się mediana.
Medianą nazywamy taką wartość zmiennej od której połowa (½) badanej zbiorowości jest niewiększa, druga połowa (½) jest większa od mediany.
Element środkowy ma wartość 6 i nieprawdą jest, że połowa badanej zbiorowości jest niewiększa od elementu środkowego (mamy na myśli osoby od 38 do 49 mieszczące się w tej samej wartości zmiennej).
Wartość realizująca się w elemencie środkowym nie spełnia warunku mediany.
D= 6 (Poziom 6).
k = 6
Rys. 4. Poziom aspiracji (zmienna ciągła bez jednostki miary - relacja porządku)
Źródło: dane umowne
Stosunek do szkoły zmienna wielkościowa (ciągła) mierzonej bez jednostki miary.
Wpisanie do tabeli wszystkich wartości zmiennej występujących w danej zbiorowości (zliczamy wszystkie 1 dla stos..1 i 2 dla stos..2 itd. dla każdej wartości zmiennej oddzielnie; wartość zmiennej ma różne kategorie np. stos. 1, stos. 2, stos. 3).
Tab. 8. Stosunek do szkoły (zmienna ciągła bez jednostki miary - relacja porządku)
Stosunek do szkoły |
ni |
Stosunek 1 |
4 |
Stosunek 2 |
34 |
Stosunek 3 |
14 |
Stosunek 4 |
28 |
Stosunek 5 |
20 |
Razem (N) |
100 |
Źródło: dane umowne
Element środkowy znajduje się więc w 50 osobie, czyli na 3 poziomie w stosunku do szkoły.
W przypadku gdy k<N (liczba wartości jest mniejsza od liczby badanych), należy sprawdzić przy wyznaczaniu kwantyli, czy jest spełniony ich warunek definicyjny.
Element o randze n spełnia warunek mediany gdy. połowa elementów w badanej zbiorowości jest nie większa od niego. Przyjmujemy wtedy, że w elemencie o randze n realizuje się mediana.
Medianą nazywamy taką wartość zmiennej od której połowa (½) badanej zbiorowości jest niewiększa (druga połowa (½) jest większa od mediany)
Element środkowy ma wartość 3 i nieprawdą jest, że połowa badanej zbiorowości jest niewiększa od elementu środkowego (mamy na myśli osoby 48 i 49 mieszczące się w tej samej wartości zmiennej).
Wartość realizująca się w elemencie środkowym nie spełnia warunku mediany.
Tab. 9. Stosunek do szkoły- liczebność skumulowana (zmienna ciągła bez jednostki miary - relacja porządku)
Stosunek do szkoły |
ni |
Liczebność skumulowana |
Stosunek 1 |
4 |
4 |
Stosunek 2 |
34 |
38 |
Stosunek 3 |
14 |
52 |
Stosunek 4 |
28 |
80 |
Stosunek 5 |
20 |
100 |
Razem (N) |
100 |
- |
Źródło: dane umowne
(Liczebność skumulowana- 4, 4+34=38; 38+14=52; 52+28=80; 80+20=100)
Wartości zmiennej, prezentowane w tabeli, można zdychotomizować (Czyli doprowadzić do zaistnienia tylko 2 wartości. Zmienna dychotomiczna ma tylko 2 wartości klasyczny przypadek to płeć ;-) zwykle).
52% respondentów wypowiedziało się pozytywnie o szkole od stopnia 3 włącznie wzwyż; natomiast 48% badanych wyraziło negatywny osąd od poniżej 3 stopnia .
Wskaźnik struktury (wi)- częstość, z jaką realizuje się wskazana wartość badanej zmiennej. Dla rozkładu wyróżniamy tyle wskaźników struktury, ile rozróżniliśmy wartości zmiennej.
wi = ( ni/N) *100%;
% = wD * 100%
wP- Wskaźnik struktury odnoszący się do najliczniejszej- pozytywnej części wypowiedzi respondentów na temat szkoły
wP = (P= 52/100)
wP = 0,52
wP = 52%
Dla ZAINTERESOWANYCH (w razie pytań lub wątpliwości proszę o kontakt e-mailowy
Można to zrobić również następująco WTEDY NALEŻY PODAĆ OBYDWA ROZWIĄZANIA
W podanym przypadku trudno zastosować podział dychotomiczny zachowując obiektywizm badawczy gdyż wiązałoby się to z zaklasyfikowaniem wartości 3 jako bardziej pozytywnej. Pozwolę sobie więc zrekodować skalę (na wzór skali Likerta- zdecydowanie tak, tak, nie wiem, nie, zdecydowanie nie) i przekształcić wartości zmiennej.
Tab. 10. Stosunek do szkoły - po przekształceniu wartości zmiennej (zmienna ciągła bez jednostki miary - relacja porządku)
Stosunek do szkoły |
ni |
Zdecydowanie pozytywny |
4 |
Pozytywny |
34 |
Po części pozytywny, Po części negatywny |
14 |
Negatywny |
28 |
Zdecydowanie negatywny |
20 |
Razem (N) |
100 |
Źródło: dane umowne
Tak więc co najmniej negatywny stosunek do szkoły wyraziło 48% respondentów; natomiast co najmniej pozytywną opinię dotyczącą instytucji wypowiedziało 38% badanych. 14% osób uczestniczących w badaniu posiada stosunek po części pozytywny, po części negatywny.
wN- Wskaźnik struktury odnoszący się do najliczniejszej- negatywnej części wypowiedzi respondentów na temat szkoły.
wN = (P= 48/100)
wN = 0,48= 48%
k = 5
Rys. 5. Stosunek do szkoły (zmienna ciągła bez jednostki miary - relacja porządku)
Źródło: dane umowne
Osiągnięcia dydaktyczne zmienna wielkościowa (ciągła) mierzonej bez jednostki miary.
Wpisanie do tabeli wszystkich wartości zmiennej występujących w danej zbiorowości (zliczamy wszystkie 1 dla neg i 2 dla przec. itd. dla każdej wartości zmiennej oddzielnie; wartość zmiennej ma różne kategorie np. neg., wys.).
Tab. 11. Osiągnięcia dydaktyczne (zmienna ciągła bez jednostki miary - relacja porządku)
Osiągnięcia dydaktyczne |
ni |
Negatywne |
36 |
Przeciętne |
49 |
Wysokie |
15 |
Razem (N) |
100 |
Źródło: dane umowne
Element środkowy znajduje się więc w 50 osobie, czyli osiągnięciach wysokich.
W przypadku, gdy k<N (liczba wartości jest mniejsza od liczby badanych), należy sprawdzić przy wyznaczaniu kwantyli, czy jest spełniony ich warunek definicyjny.
Element o randze n spełnia warunek mediany gdy. połowa elementów w badanej zbiorowości jest nie większa od niego. Przyjmujemy wtedy, że w elemencie o randze n realizuje się mediana.
Medianą nazywamy taką wartość zmiennej od której połowa (½) badanej zbiorowości jest niewiększa (druga połowa (½) jest większa od mediany)
Element środkowy ma wartość bierny i nieprawdą jest, że połowa badanej zbiorowości jest niewiększa od elementu środkowego (mamy na myśli osoby od 37 do 49 mieszczące się w tej samej wartości zmiennej).
Wartość realizująca się w elemencie środkowym nie spełnia warunku mediany.
D= negatywne
k = 3
Rys.. 6. Osiągnięcia dydaktyczne (zmienna ciągła bez jednostki miary - relacja porządku)
Źródło: dane umowne
Osiągnięcia wychowawcze zmienna wielkościowa (ciągła) mierzonej bez jednostki miary.
Wpisanie do tabeli wszystkich wartości zmiennej występujących w danej zbiorowości (zliczamy wszystkie 1 dla neg i 2 dla przec. itd. dla każdej wartości zmiennej oddzielnie; wartość zmiennej ma różne kategorie np. neg., wys.).
Tab. 12. Osiągnięcia wychowawcze (zmienna ciągła bez jednostki miary - relacja porządku)
Osiągnięcia wychowawcze |
ni |
Negatywne |
37 |
Bierny |
30 |
Aktywny |
29 |
Razem (N) |
96 |
Źródło: dane umowne
Element środkowy znajduje się więc w 48 osobie, czyli osiągnięciach biernych.
W przypadku, gdy k<N (liczba wartości jest mniejsza od liczby badanych), należy sprawdzić przy wyznaczaniu kwantyli, czy jest spełniony ich warunek definicyjny.
Element o randze n spełnia warunek mediany gdy. połowa elementów w badanej zbiorowości jest nie większa od niego. Przyjmujemy wtedy, że w elemencie o randze n realizuje się mediana.
Medianą nazywamy taką wartość zmiennej od której połowa (½) badanej zbiorowości jest niewiększa (druga połowa (½) jest większa od mediany)
Element środkowy ma wartość bierny i nieprawdą jest, że połowa badanej zbiorowości jest niewiększa od elementu środkowego (mamy na myśli osoby od 38 do 47 mieszczące się w tej samej wartości zmiennej).
Wartość realizująca się w elemencie środkowym nie spełnia warunku mediany.
D= negatywne
k = 3
Rys. 7. Osiągnięcia wychowawcze (zmienna ciągła bez jednostki miary - relacja porządku)
Źródło: dane umowne
ZAŁĄCZNIKI
Opis rozkładu zmiennych powstał na podstawie matryc:
Załącznik 1
. Charakterystyka rozkładu zmiennej jakościowej
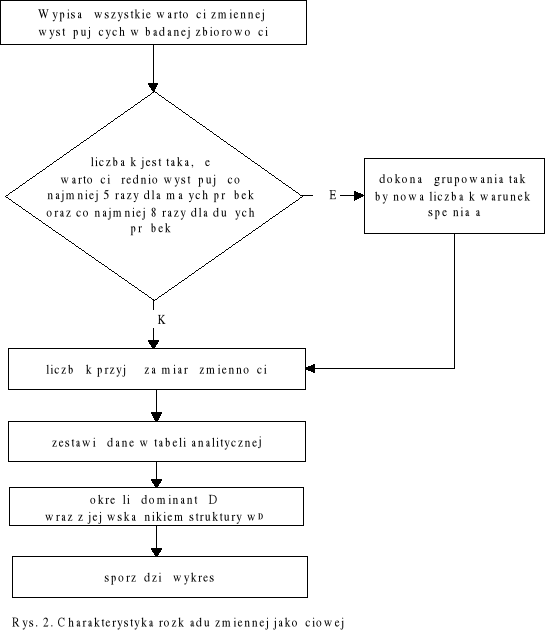
Między wartościami zmiennej jakościowej zachodzą relacje równy bądź różny, zatem rozkład takich zmiennych można charakteryzować tylko za pomocą miar kresowych.
By scharakteryzować rozkład zmiennej jakościowej, należy (patrz rys. 2.):
Załącznik 2
Charakterystyka rozkładu zmiennej wielkościowej (ciągłej) mierzonej bez jednostki miary
Charakterystyka rozkładu zmiennej ciągłej (wielkościowej) bez jednostki miary wymaga następujących operacji:
4
Wyszukiwarka