Modyfikacje Metody Składowych Atomowych Metoda z tablicą adresową Kartoteka wyszukiwawcza zostaje powiększona o tablicę adresową o takiej liczbie wierszy jaka jest liczba niepustych składowych atomowych systemu. W tablicy zapisany jest numer składowej atomowej i adres odpowiadającego jej zbioru obiektów. Odpowiadanie na pytanie zadane do systemu przebiega jak w metodzie klasycznej do momentu znalezienia numeru składowej atomowej. Następnie należy przeglądnąć tablicę adresową i jeżeli obliczony numer w niej występuje to generuje się odpowiedni zbiór obiektów wskazany tym adresem. Jeżeli obliczony numer nie występuje w tablicy adresowej to odpowiedzią jest zbiór pusty. Metoda podziału połówkowego Metodę tę można stosować dla systemu wyszukiwania bez numeracji składowych atomowych. Wtedy przy uporządkowanych opisach składowych atomowych znajdowanie odpowiedzi na term elementarny polega na porównaniu jego opisu z opisem składowej atomowej w połowie bazy danych. Przy uporządkowanym opisie składowych atomowych można stwierdzić, w której połowie bazy znajduje się szukany opis. Następnie w wybranej połowie znajdujemy właściwy opis metodą przeglądu zupełnego. Można także do wybranego fragmentu kartoteki wyszukiwawczej ponownie zastosować podział połówkowy. W przypadku k - krotnego stosowania metody podziału połówkowego trzeba przeszukać M = (L_SA/ 2^k) składowych atomowych.

Metoda odcinkowa Metoda ta pozwala przyśpieszyć wyszukiwanie odpowiedzi na pytania ogólne. Należy wybrać atrybut A_i∈A, o maksymalnej liczbie wartości. Opisy składowych atomowych są uporządkowane w ten sposób, że wybrany atrybut A_i znajduje się na pierwszym miejscu w opisie składowych atomowych, a pozostałe atrybuty są w dowolnej określonej kolejności. W ten sposób kolejne obszary pamięci są zajęte przez składowe atomowe związane z pierwszą wartością atrybutu A_i , następnie drugą wartością atrybutu A_i ... itd. Obszar pamięci zawierający składowe atomowe związane z j - tą wartością atrybutu A_i nazywa się j - odcinkiem. Adres początku i końca j - odcinka dla każdej wartości atrybutu A_i pamiętany jest tablicy adresowej. Proces wyszukiwania jest następujący:1. Dla pytań elementarnych należy znaleźć wartość atrybutu wybranego A_i w termie elementarnym a następnie odnaleźć w tablicy adresowej adres odcinka odpowiadający tej wartości atrybutu A_i , i znaleźć przeglądem zupełnym w wybranym odcinku właściwy opis składowej atomowej. Odpowiedzią na pytanie jest znaleziona składowa atomowa.2. Dla pytań ogólnych zawierających wartość atrybutu A_i , należy znaleźć zgodnie z tą wartością adres odcinka w tablicy adresowej. Znaleziony odcinek jest odpowiedzią na pytanie. Nie jest tu konieczna normalizacja termu.3. Dla pytań ogólnych nie zawierających wartości A_i , wyszukanie odpowiedzi wymaga przeprowadzenia normalizacji lub przeglądu zupełnego całości bazy danych.

Dekompozycja obiektowa Polega na podziale systemu S = < X, A, V, q > na podsystemy w taki sposób, że w każdym podsystemie znajduje się pewien podzbiór obiektów systemu S. Zbiór atrybutów i wartości atrybutów pozostaje w każdym podsystemie taki sam jak w systemie S.

Charakterystyka systemu:

S = < X, A, V, q >, S_i ⊂ S , S_i - podsystem, S =

gdzie: S_i = < X_i, A, V, q_i >, X_i ⊆ X ,

q_i = X_i × A → V, q_i = q_Xi

W tak zdekomponowanym systemie metodę składowych atomowych stosuje się w podsystemach. Każdy podsystem zawiera swój zbiór składowych atomowych i ewentualnie swoją tablicę adresową. Wyszukiwanie odpowiedzi:1. Jeżeli pytanie w postaci termu elementarnego dotyczy tylko obiektów jednego podsystemu, to odpowiedź na to pytanie znajdowane jest metodą składowych atomowych w podsystemie S_i .2. Jeżeli pytanie w postaci termu elementarnego dotyczy obiektów z kilku podsystemów to odpowiedzią na zadane pytanie suma odpowiedzi z podsystemów.

Dekompozycja atrybutowa Polega na podziale systemu S = < X, A, V, q > na podsystemy w taki sposób, że w każdym podsystemie S_i znajdują się takie same obiekty w systemie S, natomiast zbiór atrybutów i wartości atrybutów jest podzielony na różne podzbiory znajdujące się w każdym podsystemie S_i systemu S. Charakterystyka systemu:

S = , S_i = < X, A_i, V_i, q_i >,

A_i ⊆ A , , V_i ⊆ V , q_i = X × A_i → V_i, q_i = q_X×Ai

W każdym podsystemie stworzone są składowe atomowe tylko z wartości atrybutów danego podsystemu.

Wyszukiwanie odpowiedzi : 1. Jeżeli wszystkie atrybuty występujące w pytaniu składowym należą do jednego podsystemu to odpowiedź znajduje się jako składową atomową w podsystemie S_i .2. Jeżeli atrybuty termu składowego należą do kilku podsystemów to odpowiedź można uzyskać dwoma sposobami:- Odpowiedź znajduje się w podsystemach jako odpowiedź przybliżoną. Odpowiedź dokładną znajduje się przeglądem zupełnym uzyskanego zbioru składowych atomowych.- Odpowiedź znajduje się jako część wspólną odpowiedzi z kilku podsystemów. Dekompozycja hierarchiczna Może być związana z występowaniem w systemie atrybutów zależnych lub może być wymuszona. Przy dekompozycji hierarchicznej zależnej w systemie S = < X, A, V, q > zbiór atrybutów systemu może być podzielony na dwa podzbiory A*, B tak, że A=A*∪B, gdzie A* jest zbiorem atrybutów niezależnych systemu S, B jest zbiorem atrybutów zależnych systemu S. Atrybuty zależne można usunąć bez utraty informacji o obiektach systemu. Jeżeli B=B₁∪B₂∪...∪B_k, to znaczy, że wyróżnia się pewne podzbiory atrybutów zależnych w systemie S, które można uporządkować B₁⊂B₂⊂...⊂B_k. System S można zdekomponować

hierarchicznie na podsystemy S_i takie, że S_i = < X, A_i*∪B_i, V_i, q_i >, gdzie X- zbiór obiektów systemu S, B_i⊂B - zbiór atrybutów zależnych, , A_i*=A* - zbiór atrybutów niezależnych. Ostatecznie otrzymuje się ciąg podsystemów taki, że S_B1⊂S, S_B2⊂S... S_Bk⊂S , w szczególnym przypadku może być S_B1⊂S_B2⊂ ...⊂S_Bk⊂S. Zatem może zajść hierarchia wielostopniowa. Zwykle na najniższym poziomie hierarchii znajduje się system zredukowany S_A* = < X, A*,V _A*,p*>.

Odpowiedź na pytanie zadane do systemy S w zależności od zbioru atrybutów tego pytania jest odnajdywana na różnym poziomie zdekomponowanego systemu. Dekompozycja hierarchiczna wymuszona dotyczy dowolnych atrybutów systemu.

Jeżeli w pytaniu najczęściej występują razem atrybuty ze zbioru A₁⊂A, A₂⊂A, to system taki można zdekomponować atrybutowo na dwa systemy: S = S₁ ∪ S₂, gdzie S₁

= < X, A₁, V₁, q₁ >, S₂ = < X, A₂, V₂, q₂ >, A₁⊂A, A₂⊂A, V₁ ⊆ V , V₂ ⊆ V , q₁ = q_X×A1 ,q₂ = q_X×A2 . Jeżeli ponadto w pytaniach najczęściej występują razem atrybuty ze zbioru A₁₁⊂A₁ i A₁₂⊂A₁, oraz A₂₁⊂A₂ i A₂₂⊂A₂ to ostatecznie dokonana dekompozycja systemu będzie hierarchiczna. Wyszukiwanie odpowiedzi1. Jeżeli pytanie zawiera tylko atrybuty należące do określonego podsystemu to odpowiedź uzyskiwana jest bezpośrednio z tego podsystemu.2. Jeżeli pytanie zawiera atrybuty należące do kilku podsystemów to odpowiedź uzyskiwana jest jako przecięcie odpowiedzi z odpowiednich podsystemów. Parametry Metody Składowych Atomowych

Struktura bazy danych Struktura bazy danych jest prosta w metodzie klasycznej, staje się bardziej złożona w modyfikacjach.

Redundancja i zajętość pamięci Klasyczna metoda nie wnosi redundancji. Redundancja może wystąpić w dekompozycji obiektowej i atrybutowej. Zajętość pamięci jest największa w metodzie klasycznej i przy dekompozycji atrybutowej. W pozostałych modyfikacjach nadmiarowość jest niewielka. Proces aktualizacji Wprowadzenie nowego obiektu do bazy danych w metodzie klasycznej wymaga:

- obliczenia numeru składowej atomowej odpowiadającemu opisowi obiektu- wprowadzenia obiektu do obliczonej składowej atomowej

W metodzie z tablicą adresową należy sprawdzić czy obliczony numer występuje w tablicy adresowej. Jeśli występuje to należy dopisać obiekt pod wskazany adres, gdy nie ma obliczonego numeru to należy go dopisać i przyporządkować mu adres obiektu. W metodzie odcinkowej po znalezieniu odpowiedniego odcinka dopisuje się do niego nowy obiekt. W dekompozycji obiektowej obiekt należy dopisać do odpowiedniego podsystemu. W dekompozycji atrybutowej należy obiekt wpisać do każdego podsystemu. Usuwanie obiektu w metodzie klasycznej wymaga:- obliczenia numeru składowej zgodnie z opisem obiektu- usunięcia obiektu z odpowiedniej składowej. W modyfikacji z tablicą adresową należy znaleźć obliczony numer składowej w tablicy adresowej i odnajdując adres składowej usunąć z niej obiekt. Może to doprowadzić także do usunięcia składowej atomowej z tablicy adresowej. W metodzie odcinkowej w opisie obiektu wyodrębniamy wartość wybranego atrybutu. Znajdujem odcinek odpowiadający tej wartości i z odcinka usuwamy wskazany obiekt. W metodzie z dekompozycją obiektową postępowanie jest jak w metodzie klasycznej tylko w odpowiednim podsystemie. W metodzie z dekompozycją atrybutową należy usunąć obiekt we wszystkich podsystemach .Zmiany w opisie obiektu sprowadzają się do usunięcia tego obiektu i wpisania obiektu o nowym opisie. Czas wyszukiwania Metoda składowych atomowych ma krótsze czasy wyszukiwania odpowiedzi na pytania elementarne niż na ogólne z wyjątkiem modyfikacji odcinkowej i dekompozycji atrybutowej. Język wyszukiwawczy W systemie opartym na metodzie składowych atomowych stosowany jest język deskryptorowy. Tryb pracy Preferowany jest tryb pracy wsadowej.

SAMART

NAJBARDZIEJ ISTOTNE SŁOWNIKI Zalety słowników (głównie synonimów i fraz):1.Pozwalają na przyporządkowanie terminom pewnych klas pojęć eliminując potrzebę użycia słów kluczowych lub terminów indeksowych. Słownik są pomocne do usuwania niejednoznaczności w tekscie, albowiem badają okoliczności występowania pojęć. Słowniki te mogą służyć do analizy tekstu w wielu dziedzinach ponieważ są łatwo adaptowalne w określonej dziedzinie. ZASADY TWORZENIA SŁOWNIKÓW Zasady tworzenia Tezaurusa (słownika synonimów).Słownik ten jest zbiorem słów jest tematem słów ujętych w pewne kategorie tematyczne zwane klasami pojęć. Klasy są reprezentowane przez liczby a poszczególne pozycje występujące w klasie są wymieniane pod numerem pojęcia wymienionego w tezaurusie. Istotne problemy występujące przy tworzeniu tezaurusa: Które słowa powinny być wyszczególnione w tezaurusie (wiąże się z tworzeniem szerokich i wąskich klas pojęć) ? Jakie kategorie synonimów należy pamiętać w tezaurusie ? Gdzie umieścić określone słowo - tzn. w której klasie pojęć ?Konieczność przeanalizowania słów zabronionych (słów, które nie wnoszą informacji). Konieczna analiza terminów niejednoznacznych (każda klasa pojęć powinna zawierać tylko terminy o zbliżonych częstotliwościach tzn. każda klasa powinna zawierać także terminy, których charakterystki relewancji są w przybliżeniu podobne.

Konieczność współpracy lingwistów i specjalistów z dziedziny, której dotyczy system. Tezaurus tematyczny składa się z listy słów zawartych w typowym zbiorze dokumentów charakterystycznych dla danej dziedziny, przy czym każdy temat ma określony numer w tezaurusie tematycznym odpowiadający numerowi pojęć w normalnym tezaurusie, przy czym jeden numer w tezaurusie tematycznym odpowiada wiele numerów w tezaurusie normalnym. Tezaurus tematyczny należy rozróżnić od tezaurusa tematów - słownika tematów słów bez przed i przyrostków, które to znajdują się w oddzielnych słownikach. Słownik fraz Frazy składają się z kombinacji słów, które uważa się za istotne w danej dziedzinie tematycznej. Słownik fraz pozwala zidentyfikować frazę na podstawie kombinacji pojęć. W słowniku fraz występują: pary, trójki, czwórki pojęć, które odpowiadają frazom najbardziej oczekiwanym w tekstach z danej dziedziny. Istotne frazy w tekście można wykryć na podstawie jej składowych bez względu na relację między nimi. Są dwa typy tworzonych fraz: słownik fraz statystycznych; słownik fraz syntaktycznych. Słownik oparty jest na algorytmach rozpoznawania fraz w tekście jedynie na podstawie charakterystyki łącznego występowania pojęć. W słownik fraz syntaktycznych każda fraza składa się z wyszczególnionych pojęć, wskazań syntaktycznych i relacji syntaktycznych, ktore mogą zachodzić pomiędzy składowymi frazy. Hierarchiczna organizacja pojęć Słownik „Hierarchiczna organizacja pojęć” jest tworzony na podobnej zasadzie jak hierarchiczna klasyfikacja haseł przedmiotowych w bibliotekoznawstwie. Klasyfikacja ta umożliwia ustawianie pojęć bardziej szczegółowych pod ogólnymi i formułowanie zadań od bardziej ogólnych do zadań bardziej szczegółowych. Hierarchiczna organizacja pojęć może być używana od identyfikacji pojęć jak i do jego wyszukiwania. Pojęcia ogólne i najbardziej szerokie umieszcza się po lewej stronie i odpowiadają one pniu drzewa, ima bardziej szczegółowe pojęcie tym umieszczone jest z prawej strony, dalej od pnia. Dla ułatwienia procesu identyfikacji, wyszukiwania pojęcia są zapisywane w postaci numerów. Przeprowadzono wiele prób hierarchi organizacji pojęć. Istenieją pewne algorytmy tworzenia hierarchicznej organizacji pojęć lecz nie są one optymalne, ponieważ można się tylko kierować ogólnymi zasadami: pojęcia ogólne i najbardziej szerokie umieszcza się po lewej stronie i odpowiadają one pniu drzewa, ima bardziej szczegółowe pojęcie tym umieszczone jest z prawej strony, dalej od pnia, pojęcia występujące najczęściej w dokumentach danej dziedziny powinny być na najwyższym poziomie hierarchii - w pniu, jak najbliżej pnia. AUTOMATYCZNE TWORZENIE TEZAURUSA Ze względu, że tworzenie tezaurusa wymaga ogromu pracy specjalistów z danej dziedziny, dla której tworzony jest tezaurus oraz innych, zostały stworzone dwie metody pozwalające na automatyczne tworzenie tezaurusa: metoda pozwalająca na automatyczne tworzenie tezaurusa metota pozwalająca na półautomatyczne tworzenie tezaurusa. Dla automatycznej metody tworzenia tezaurusa postępuje się w następujący sposób: Wyszukuje się zbiór dokumentów, który jest reprezentatywny dla danej dziedziny. Zlicza się częstość występowania słów w tym zbiorze dokumentów, następnie określa się zbiór słów najczęściej występujących w danym dokumencie.

Tworzy się następnie macierz termin-dokument jak np.

	T1	T2	T3	T4	T5	T6	T7
D1	3	0	0	2	0	6	1
D2	0	0	1	3	2	0	2
D3	0	2	3	0	4	0	0
D4	1	2	1	6	3	1	0

gdzie: T₁ . . . T₇ - zbiór terminów najczęściej występujących terminów; D₁ . . . D₄ - zbiór dokumentów Element występujący na przecięciu i-tego wersu i j-tej kolumnt reprezentuje wagę terminu j-tego w dokumencie i-tym. Waga określa częstość występowania terminu w dokumencie. Na podstawie macierzy termin-dokument tworzy się graf dokument termin. W grafie dokument-termin węzły reprezentują dokumenty, a łuki reprezentują terminy, które występują w tych dokumentach z określoną wagą.

Na podstawie macierzy termin-dokument i grafu dokument-termin określamy współczynnik podobieństwa pomiędzy terminami, przy czym współczynniki podobieństwa określane są poprzez występowanie tych terminów w innych dokumentach z podobną częstością. Poprzez analizę współczynników podobieństwa tworzy się tzw. kategorię pojęć.T₁' ⇒ (T₁ , T₆) ; T₂' ⇒ (T₄ , T₇) ; T₃' ⇒ (T₂ , T₃ , T₅)

W naszym wypadku otrzymaliśmy trzy kategorie pojęć. Na ich podstawie tworzy się kolejny graf. W nowoutworzonym grafie węzłami są kategorie pojęć, natomiast przy łukach umieszcza się dokumenty, które są reprezentatywne dla tych kategorii. Na podstawie tych pojęć tworzy się kategorie tezaurusa, a termy występujące w kategoriach umieszczone są jako pojęcia szczegółowe w danej klasie. Możliwe jest również utworzenie grupy z dokumentami niezwiązanymi. Analiza grafu służy do weryfikacji zastosowanej metody automatycznego tworzenia tezaurusa. Widać, że metody automatyczne są zawodne, albowiem tworzenie kategorii opiera się na założeniu, że łączne występowanie terminów w dokumentach i ze zbliżoną częstością świadczy o jakimś ich podobieństwu i zalicza do tej samej kategorii - co nie zawsze jest słuszne - stąd propozycja metod półautomatycznych. metodach półautomatycznych tworzenia tezaurusa najpierw przeprowadzamy automatyczną metodę tworzenia tezaurusa a następnie przeprowadza się weryfikację utworzonych kategorii z udziałem ekspertów, z dziedziny dla której jest tworzony tezaurus. Weryfikację przeprowadza się w trzech etapach:

Ekspert określa, czy pojęcia zaliczone do tej samej kategorii nie są synonimami. Czy te pojęcia mogą należeć do tej samej klasy tezaurusa. Drugi etap polega na sprawdzeniu czy otrzymane terminy można zaliczyć do tych samych struktur syntaktycznych, czy terminy należące do tych samych struktur syntaktycznych zalicza się do tej samej klasy tezaurusa. Przygotowuje się szczegółowo opracowany zbiór pytań dla uzyskania informacji o proponowanych kategoriach. Odpowiedzi eksperta powinny pozwolić na potwierdzenie zaliczenia terminu do danej kategorii lub odrzucenie tego założenia. OPIS METODY WYSZUKIWANIA (tworzenie kartoteki wyszukiwawczej, proces wyszukiwania) System wyszukiwania informacji zadany jest jak w innych systemach, poprzez określenie zbioru X, zbioru atrybutów A, zbioru wartości V oraz funkcji informacji ρ - S = < X, A, V, ρ > . W systemie Saltona zbiorem obiektów X jest zbiór dokumentów w języku naturalnym. Funkcja informacji ρ określa opis danego dokumentu.

W metodzie Saltona wszystkie obiekty (dokumenty) dzieli się na podgrupy X_i (i = 1 . . . m), przy czym te podgrupy stanowią pewne grupy dokumentów podobnych.

Każda utworzona grupa X_i składa się z reprezentanta C_i , który jest nazywany centroidem i ze zbioru obiektów (dokumentów) należących do tej grupy. W miejsce centoida (C_i) może występwać profil grupy P_i.

X_i = (C_i, {t_Xi}).

Centroid jest pewnym zbiorem pojęć (wykorzystywany w algorytmie Rocchia), a profil jest jego odpowiednikiem (kodem) numerycznym (ewentualnie numerem grupy), tworzonym w grupowaniu algorytmem Doyle'a. Istnieje wiele algorytmów grupowania, przy czym najbardziej popularne i najczęściej używane są dwa: algorytm Rocchia i algorytm Doyle'a. W algorytmie Rocchia (jak już wcześniej wspomniano) reprezentatem grupy jest centroid, zaś w algorytmie Doyle'a reprezentatem grupy jest profil. Proces zakładania kartoteki wyszukiwawczej polega na przeprowadzeniu algorytmu grupowania dokumentów jedną z dwóch powyższych metod. Po założeniu kartoteki wyszukiwawczej proces wyszukiwania może być przeprowadzony metodą sekwencyjną lub metodą strukturalną. Metoda strukturalna jest orginalną metodą Saltona (metoda wyszukiwania Saltona). ZAKŁADANIE KARTOTEKI WYSZUKIWAWCZEJ Algorytm Rocchia (algorytm wiązania dokumentów w grupy) Spośród wszystki dokumentów niezwiązanych wybieramy dokument, ktory stanowi przypuszczalne centrum grupy i obliczamy współczynnik korelacji tego dokumentu ze wszystkimi dokumentami tego zbioru. Wybrany dokument poddajemy testowi gęstości. Test ten mówi, że co najmniej N₁ dokumentów musi mieć współczynnik korelacji z wybranym dokumentem większy bądź równy od założonego parametru p₁ i co najmniej N₂ dokumentów musi mieć współczynnik korelacji z wybranym dokumentem większy bądź równy od założonego parametru p₂, gdzie spełnione są następujące warunki: N₁ ≥ p₁ N₂ ≥ p₂ p₂ > p₁ N₂ < N₁ . Test ten gwarantuje, że dokumenty z brzegu grup nie będą wybrane jako centrum. Jeżeli wybrany dokument przeszedł test gęstości - został uznany jako centrum grupy, to na podstawie rozpiętości granic grupy i rozkładów współczynnika korelacji określa się wartość progową współczynnika korelacji p_min. p_min będzie równe p₁ (p_min = p₁) jeśli mniej dokumentów niż wynosi minimalny rozmiar grupy ma współczynnik korelacji większy od p₁. W każdym innym przypadku p_min wybiera się jako współczynnik korelacji dokumentu, przy ktorym nastąpiła największa różnica pomiędzy kolejnymi współczynnikami korelacji dokumentów sąsiadujących z grupą maksymalną. Liczba dokumentów w grupie minimalnej jest określana jako M₁, zaś grupy maksymalnej jako M₂. Tworzymy wektor centroidalny, czyli centroid z terminów czy pojęć tych dokumentów, które należą do grupy minimalnej.

W metodzie list prostych kartoteka wyszuk. jest równoznaczna z kartoteką wtórną. Wyszukiwanie odpowiedzi na pytanie t może być realizowane dwoma sposobami: -przeglądamy kolejne opisy obiektów i wybieramy obiekty zawierające w swoim opisie pierwszy term składowy pytania. - porównujemy pytanie (pełne) t z kolejn-

-ymi opisami obiektów i wybieramy obiekty zawierające w swoim opisie przynajmniej jeden term składowy pytania t. Sposoby te różnią się jedynie czasem wyszukiwania i nie można ogólnie stwierdzić, który z nich jest szybszy. Jeżeli w skład pytania t wc- -odzi dokładnie jeden term składowy to działanie obu metod jest identyczne. Algorytm wyszukiwania : 1.pobierz pierwszy dokument (opis obiektu)2. pobierz pierw. deskryptor pytania 3. pobierz pierw- -szy deskryptor opisu obiektu 4.dokonaj porównania deskryptorów: a) jeśli są „=” pobierz kolejny deskryptor pytania i przejdź do p.3; jeżeli koniec pytania, to dołącz identyfikator obiektu do zbioru odpowiedzi i przejdź do p. 5; jeżeli koniec kartoteki wyszukiwawczej, przejdź do p. 6, b) jeżeli są <>, pobierz kolejny deskryptor opisu obiektu i przejdź do p.4; jeżeli sprawdzono cały opis obiektu, przejdź do p.5. 5. jeżeli sprawdzono wszystkie dokumenty to idź do p.6 w przeciwnym wypadku pobierz

kolejny dokument i powróć do 2.6) Zakończ wyszukiwanie

AKTUALIZACJA

Proces aktualizacji w przypadku klasycznej metody list prostych jest bardzo prosty. W przypadku dodawania nowego obiektu po prostu dopisuje się ten obiekt jako ostatni. W przypadku usuwania proces składa się z wyszukania obiektu i usunięcia go. W przypadku modyfikowania obiektu można to zrobić przez usunięcie tego obiektu i dopisanie go ze zmodyfikowanymi wartościami na końcu.

PARAMETRY LIST PROSTYCH Czas wyszukiwania jest dość długi
, gdzie N - liczba obiektów systemu, τ₀ - czas sprawdzania opisu obiektu Redundancja nie występuje w klasycznej metodzie list prostych.Tryb pracy systemu : brak preferencji - zarówno w trybie pracy ciągłej jak i wsadowej. MODYFIKACJE

ODCEDZANIE Idea odcedzania polega przez odpowiednie uszeregowanie obiektów można zapewnić przyspieszenie pracy sys. Jednak sys. musi spełniać pewne warunki, a mianowicie musi istnieć pewna grupa pytań typowych dla tego systemu, tj. takich, które powtarzają się najczęściej. Rozróżniamy 3 odmiany odcedzania: Odcedzanie Statyczne, Dynamiczne i Hiperdynamiczne. Odcedzanie Statyczne polega na tym, że po ustaleniu grupy pytań ustala się które obiekty są najczęściej relewantne i uszeregowuje je się od najczęściej do najrzadziej występującego. Odcedzanie Dynamiczne charakteryzuje się tym, że po każdym pytaniu Sys sam się przeszeregowuje podnosząc częściej występujące obiekty wyżej, a opuszczając rzadziej występujące obiekty. Odcedzanie Hiperdynamiczne jest ulepszoną formą odcedzania dynamicznego. Odcedzanie dynamiczne ma tę wyższość nad statycznym, gdy zmienią się pytania system natychmiast jest w stanie się przestawić na nowe typowe pytania, natomiast w przypadku statycznego dopiero po ustaleniu grupy można przeanalizować system i ewentualnie posortować.

ODCEDZANIE HIPERDYNAMICZNE

Algorytm Odcedzania Hiperdynamicznego jest prosty. Po wyszukaniu obiektów relewantnych do pytania, należy wszystkie te obiekty przesunąć na pierwsze miejsca. Np. Jeśli obiekty relewantne były na pozycjach 1, 7 , 9, 11 to po odcedzaniu będą odpowiednio na pozycjach 1,2,3,4 przy czym istotne jest to że obiekt na pozycji 9 nie może wyjść wyżej od obiektu na pozycji 7.Jak widać po przeprowadzeniu serii można zaobserwować stan pewnej stabilizacji. Obiekty nie używane są na dalszej pozycji i tam pozostaną dopóki nie pojawi się pytanie wobec którego będą obiektami relewantnymi. Obiekty relewantne wobec większości pytań (np. 25,26,27) oscylują w pobliżu początku co jest korzystne i jak najbardziej pożądane. Podstawową wadą, ale jednocześnie jego największą zaletą jest dynamiczność. Tzn. w wypadku gdy pojawi się jakieś niestandardowe pytanie to w przypadku odcedzania statycznego nie zmieniło by to kompletnie ułożenia sys a w przypadku dynamicznego spowolniłoby następne wyszukiwania. Jednakże odcedzanie statyczne jest możliwe dopiero po ustaleniu pewnej grupy pytań, które być może już są nieistotne i będą przeszkadzać w normalnej pracy. Powiedzmy. że proces odcedzania odbywa się rano i w południe (system czynny od rana do wieczora). Rano system otrzymuje pytania dotyczące powiedzmy broni jednoręcznych tnących, lekkich i zadających niewiele obrażeń, po południu przychodzi grupa, która zadaje pytania całkowicie przeciwne (bronie dwuręczne kłute wolne ciężkie, zadające dużo obrażeń) a sys przeanalizował dotychczasowe serie pytań i uszeregował bazę w sposób wspaniale spowalniający pracę bowiem informacje potrzebne grupie popoł. znajdują się dokładnie na końcu. Rano, sys ponownie analizuje system i powtórnie utrudnia działanie. Oto przykład, gdzie odcedzanie przynosi efekt całkowicie odwrotny od zamierzonego. W przypadku odcedzania dynamicznego (Hiperdynamicznego) sytuacja jest inna, po pierwszych kilku pytaniach, obiekty niepotrzebne DANEJ grupie przesuwają się w dół, a na ich miejsce przypływa potrzebna informacja. Tak więc system dynamicznie odcedzany jest bardzo wrażliwy na zadawane pytania i natychmiast usiłuje zareagować w sposób jak najlepszy dla użytkownika. Oczywiście w przypadku, gdy przedstawiciele obu grup będą naprzemian pytać o sprzeczne obiekty, system również będzie spowalniał pracę, nie bardziej jednak od odcedzania statycznego. UPORZĄDKOWANIE OPISÓW OBIEKTÓW

Jeżeli spojrzymy na kartotekę wyszukiwawczą załączoną do sprawozdania zauważymy, że jest ona już w pewien sposób uporządkowana. Konkretniej, wszystkie deskryptory są ułożone w określonej kolejności. Zostało to niejako wymuszone przez zastosowanie tabeli, a ponadto ze względu na wygodę posługiwania się takim sposobem. Poza tym zastosowanie uporządkowania niesie ze sobą przyspieszenie porównywania termu z deskryptorem (pod warunkiem, że termy pytania są uporządkowane w identyczny sposób) GRUPOWANIE OBIEKTÓW WEDŁUG WYBRANEGO ATRYBUTU Aby zastosować tą modyfikację, należy najpierw wybrać atrybut wg którego będziemy grupować bazę danych. Żeby grupowanie przyniosło korzyści atrybut powinien:- mieć dużą liczbę wartości

- w ramach wartości liczba obiektów relewantnych powinna być porównywalna ze sobą - najczęściej występować w pytaniach

Pierwszy warunek pozwala uzyskać niewielkie grupy do przeszukiwania, drugi - że obiekty zostaną równomiernie rozłożone między grupy (gdyby atrybut np. a dzielił 100 obiektów na 10 grup, a w ramach pierwszej grupy byłoby 80 obiektów, to korzyści byłyby żadne), a trzeci - pozwala uniknąć konieczności przeszukiwania całej bazy danych. Charakterystyczna dla tej metody jest tablica adresowa. Jest to tablica, która zawiera wszystkie wartości wybranego atrybutu oraz adres pierwszego obiektu relewantnego w systemie a także adres ostatniego lub po prostu ilość tych obiektów. W porównaniu do klasycznej metody modyfikacja charakteryzuje się szybkością, przy jednoczesnym nie zwiększeniu redundancji. Jedyną wadą tej modyfikacji jest utrudnienie aktualizacji, a konkretniej dopisywania. Bo o ile przy usuwaniu czy modyfikowaniu nic nie przeszkadza w normalnym procesie (przy modyfikowaniu bezpośrednio na obiekcie deskryptorów różnych od wybranego) to przy dopisywaniu i modyfikacji przez usunięcie i dopisanie oraz modyfikowaniu deskryptora wybranego istotne jest miejsce w bazie, gdzie będzie dopisany obiekt. Tzn. Problem leży jedynie w tym, że przed dopisaniem należy znaleźć grupę do której zakwalifikujemy dany obiekt i następnie dopisać go jako ostatni w danej grupie oraz zaktualizować tablicę adresową

Algorytm wyszukiwania w zmodyfikowanej metodzie list prostych - grupowaniu zależy od tego, czy w pytaniu występuje atrybut wybrany do grupowania. Jeśli nie, traktujemy system tak jakby nie był w ogóle zmodyfikowany czyli stosujemy przegląd zupełny, natomiast jeśli występuje to odwołujemy się do tablicy adresowej i ograniczam przegląd jedynie do danej grupy.

Klasyczna metoda Luma jest rozszerzeniem metody list inwersyjnych. Polega ona na tworzeniu zbiorów podobnych list jak w metodzie list inwersyjnych, przy czym każda z nich odpowiada określonej kombinacji wartości atrybutów.

Założenia:

Opis grupy jest postaci

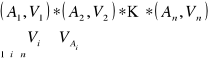
gdzie:

to znaczy: opis grupy jest iloczynem deskryptorów z każdego atrybutu. Kolejność atrybutów w systemie jest z góry ustalona, a wartości są ponumerowane w obrębie danego atrybutu. Struktura bazy danych Kartoteka źródłowa zawiera dokumenty w postaci źródłowej, opisane w języku naturalnym. Kartoteka wtórna to zbiór opisów

biektów w postaci deskryptorowej. W kartotece wyszukiwawczej pamiętane są numery grup i zbiory adresów obiektów odpowiadające każdej grupie. Opisy grup są iloczynami deskryptorów z każdego atrybutu i są uporządkowane w sposób leksykograficzny (stąd jednoznaczna numeracja). Kolejne opisy grup można przedstawić w postaci:

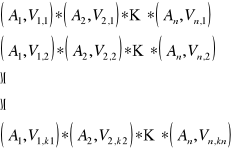
Liczbę grup oblicza się ze wzoru

gdzie m₁ oznacza liczność zbioru wartości i - tego atrybutu, m_i=card V_ai Numer grupy obliczamy ze wzoru:

j_k - j-ta wartość k-tego atrybutu, występującego w pytaniu.

m_k=card V_Ak N - adres pierwszej grupy

Każda grupa jest identyfikowana przez swój adres. W bazie danych występuje duża liczba grup pustych, których opisy nie odpowiadają opisom żadnego z obiektów.

Metoda Chowa

Metoda Chowa jest typową metodą grupowań, gdyż jak w metodzie Ghosha kartotekę wyszukiwawczą tworzymy poprzez grupowanie obiektów w określone klasy i grupy. Polega ona na podziale wszystkich obiektów bazy danych na zadaną z góry liczbę r rozłącznych grup.

W systemie wyszukiwania informacji S = < X,A,V,ρ > określony jest zbiór obiektów X , atrybutów A, wartości atrybutów V, a także funkcja ρ, to znaczy zadany jest opis deskryptorowy każdego obiektu. W systemie wyodrębniony jest dodatkowo zbiór wszystkich deskryptorów systemu D = {d­­­₀ , ... , d_n-1 }, gdzie d_i = (a_i ,v_{i j}), a_i ∈ A , a v_{i j} oznacza j-tą wartość i-tego atrybutu. Wszystkie obiekty systemu grupujemy w klasy. Opisy klas są iloczynami k-deskryptorów. W systemie o n-deskryptorach liczba wszystkich takich klas jest równa :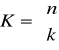

Utworzone klasy grupujemy następnie w założoną liczę r grup. W każdej grupie znajdzie się :

.

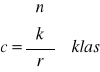
Jeżeli c jest liczba całkowitą, to każda grupa zawiera c klas. Jeżeli c nie jest liczbą całkowitą, to pierwszych r-1 grup zawierać będzie c -1 klas, a ostatnia grupa - pozostałe.{ n - kres górny z liczby n }Wszystkie deskryptory systemu numerujemy od 0 do n-1. Opisy klas są postaci : d_{i 1} ­^. d_{i 2} ,...,d_{i k} . W opisach klas przyjmujemy uporządkowanie i₁ < i₂ < ... < i_k .Uporządkowanie klas jest również rosnące, np. d₀ ­­^. d₁ ^. d₂ poprzedza d₁ ^. d₂ ^. d₃ itd. Klasy te następnie łączymy w grupy. Większość tak utworzonych klas będzie klasami pustymi z założenia (opisy będą iloczynami tych samych atrybutów.

Ostatecznie w kartotece wyszukiwawczej pamiętane są numery grup, numery klas i odpowiadające klasą zbiory obiektów (opisy klas nie są pamiętane). Struktura bazy danych jest bardzo prosta po założeniu, jednak jest dość sztywna. Proces zakładania bazy danych wymaga dokonania klasyfikacji obiektów w grupy i klasy oraz numeracji klas i grup. Tworzenie klas i grup jest szybkie. Metoda klasyczna nie wnosi redundancji. Redundancja wystąpi, gdy długość opisów jest większa niż długość opisu klasy. Istotną wadą metody Chowa jest duża zajętość pamięci. Nadmiarowość zajmowanej pamięci wyraża wzór :

m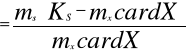
,

gdzie : K_S - liczba klas w systemie ,

m _S - średnia liczba jednostek pamięci zajmowanych przez klasę,

m_X - średnia liczba jednostek pamięci związanych z zapisem jednego obiektu. Nadmiarowość w modyfikacji z nie pamiętaniem klas pustych:

m₁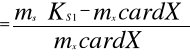
,

gdzie: K_S1 - liczba klas w systemie zmodyfikowanym,

K_S1 < K_S , stąd m₁ < m .

Dla modyfikacji z tablicą adresową zajętość pamięci określa wzór:

z = m_X * cardX + m_t ,

gdzie : m_t - miejsce konieczne do zapamiętania tablicy adresowej.

Nadmiarowość można zatem wyrazić jako:

m₂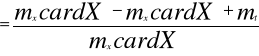
,

m₂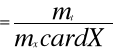
,

Zwykle zachodzi m_t < m .

Jak widzimy modyfikacje znacznie zmniejszają zajętość pamięci. Proces aktualizacji jest dość złożony. Wprowadzenie nowego obiektu wymaga znalezienia numeru klasy i grupy, do której obiekt należy wprowadzić. W przypadku, gdy obliczona klasa jest niepusta, dopisujemy obiekt do klasy i może wystąpić konieczność zmiany adresów grup i klas (przy braku miejsca w danej klasie). W modyfikacji z tablicą adresową problem ten jest łatwy do rozwiązania, gdyż o adresach decyduje tablica adresowa. Usunięcie obiektu może

spowodować powstanie klasy pustej. Zmiany w opisie obiektu wymagają usunięcia obiektu o nieaktualnym opisie i dopisania nowego obiektu do odpowiedniego miejsca w kartotece wyszukiwawczej.

Czas wyszukiwania odpowiedzi na pytanie o długości opisu klasy jest bardzo krótki, można go wyrazić wzorem:

τ = τ_N + τ_c + τ_G ,

gdzie : τ_N - czas potrzebny na znalezienie numeru klasy , τ_c - czas potrzebny na sprawdzenie warunku na liczbę klas w grupie, τ_G - czas niezbędny na obliczenie numeru grupy.Czasy te zależą głównie od szybkości maszyny cyfrowej i : τ_N > τ_c , τ_N > τ_G . Zatem τ ≈ τ_N .

W modyfikacji z przydziałem klas do grup (modulo r) nie występuje czas τ_c , natomiast w modyfikacji z tablicą adresową należy uwzględnić czas przeglądu tablicy τ_t :

τ­' ≅ τ_N + τ_t , τ­' > τ.

Czas wyszukiwania dla pytań dłuższych niż długość opisu klasy :

τ_S = τ + τ_p ,

gdzie : τ_p - czas przegl --> [Author:RC] ądu zupełnego obiektów wybranej klasy.

Czas wyszukiwania dla pytań ogólnych :

τ₀ ≈ τ_n + m*τ ,

gdzie : τ_n - czas normalizacji pytania , m - liczba termó --> [Author:RC] w po normalizacji .

Zależność pomiędzy poszczególnymi pytaniami :

τ < τ_S < τ₀ .

Do opisów obiektów, jak i dla zadawania pytań preferowany jest język

deskryptorowy. Metoda Chowa może być stosowana w pracy ciągłej

jak i wsadowej. Tryb wsadowy jest dogodniejszy ze względu na

proces aktualizacji.

Charakterystyka metody list inwersyjnych

W metodzie list inwersyjnych kartoteka wtórna niczym się nie różni od kartoteki z metody list prostych (obiekty pojawiają się zgodnie z kolejnością ich napływania), natomiast kartoteka wyszukiwawcza jest zakładana w specjalny sposób:

Funkcja adresująca: μ : X→N (przyporządkowanie adresu obiektowi)

μ (x) = μ (y) ⇔ t_x= t_y x, y ∈ X

Obiekty mają ten sam adres, jeśli posiadają identyczny opis deskryptorowy.

Tworzymy listy adresów tych obiektów, które w swoim opisie zawierają deskryptor . Listy takie nazywamy listami inwersyjnymi:

Utworzony zbiór obiektów stanowi kartotekę wyszukiwawczą w systemie. Przy niewielkiej liczbie obiektów można wprost pamiętać obiekty.

Proces wyszukiwania w metodzie list inwersyjnych

1. Pytanie ogólne - suma termów składowych

2. Pytanie szczegółowe

Aktualizacja

Proces aktualizacji w przypadku klasycznej metody list inwersyjnych jest identyczny jak w metodzie list prostych z małym uzupełnieniem. W przypadku dodawania nowego obiektu po prostu dopisuje się ten obiekt jako ostatni. W przypadku usuwania proces składa się z wyszukania obiektu i usunięcia go. W przypadku modyfikowania obiektu można to zrobić przez usunięcie tego obiektu i dopisanie go ze zmodyfikowanymi wartościami na końcu. Te operacje są przeprowadzane na kartotece wtórnej, natomiast w kartotece wyszukiwawczej tj. listach muszą zostać zaktualizowane deskryptory opisujące obiekt dopisywany, usuwany lub modyfikowany.Tak więc dla obiektu dopisywanego: w każdej liście z deskryptorem do którego obiekt jest relewantny dopisywany jest adres tego obiektu; dla usuwanego obiektu -usuwa się adres tego obiektu z list zawierających adres tego obiektu; a dla modyfikacji - z danej listy jest usuwany adres i dopisywany jest on do innej.

Parametry metody list inwersyjnych

Czas wyszukiwania jest zależny od typu pytania - czas odpowiedzi na pytanie ogólne jest czasem krótkim, zależy tylko od czasu generacji poszczególnych list; natomiast dla pytań szcegółowych dochodzi do tego jeszcze czas przecinania list.

Przyspieszenie pracy sytemu odbywa się niestety kosztem redundancji:

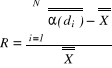
Również zwiększona zajętość pamięci jest ceną którą trzeba zapłacić za szybkość.

Preferowany tryb pracy systemu : praca wsadowa.

MODYFIKACJE

Modyfikacja metody list inwersyjnych ze zmniejszoną ilością generowanych list Podstawowymi wadami metody list inwersyjnych są: nadmierna redundancja i zajętość pamięci. Aby zmniejszyć te dwa parametry, nie tracąc zbytnio na szybkości można zastosować właśnie tą modyfikację. Polega ona na tym, że w zbiorze deskryptorów wyodrębniamy podzbiór i listy inwersyjne są tworzone dla wszystkich deskryptorów należących do D' a nie do D jak w metodzie klasycznej. Wybrany zbiór D' może być zbiorem deskryptorów najczęściej występujących w pytaniach do systemu S lub

zbiorem deskryptorów pewnego atrybutu (pewnych atrybutów). W omawianej modyfikacji tworzymy listy inwersyjnych α(d_i), gdzie di ∈ D' i

Pytanie do systemu zadajemy w postaci termu t. Zakładamy, że tak jak w metodzie klasycznej list inwersyjnych (bez modyfikacji) term t ma postać termów składowych t = t₁ + t₂ + . . . + t_m .

Należy tu rozpatrzyć kilka przypadków:

Wszystkie deskryptory termów składowych zawierają się w D'. Jest to najlepszy możliwy przypadek. W tej sytuacji szybkość systemy jest maksymalna. Postępuje się jak w klasycznej metodzie list inwersyjnych. Część deskryptorów zawiera się w D'. Najpierw dokonuje się odpowiedzi przybliżonej, tj ignoruje się wszelkie deskryptory, które nie należą do D', a następnie te zignorowane deskryptory uzyskanych obiektach porównuje się wprost z pominiętymi deskryptorami pytania. Żaden z deskryptorów nie zawiera się w D'. Jest to najbardziej niesprzyjający przypadek. W tej sytuacji należy dokonać przeglądu zupełnego (czyli potraktować kartotekę wtórną jako wyszukiwawczą i wykorzystać klasyczną metodę list prostych). Ponieważ w trzecim przypadku przy pewnej redundancji i zajętości pamięci nie skorzystaliśmy z szybkości należy tak wyodrębnić podzbiór D', aby przypadek trzeci zdarzał się bardzo rzadko (a najlepiej nigdy). Opisana modyfikacja ze względu na zmniejszoną liczbę list inwersyjnych daje wyraźną poprawę redundancji. Właściwe dobranie zbioru D' decyduje o efektywności opisanej modyfikacji (przypadek przeglądu zupełnego występuje bardzo rzadko). Zmniejszenie redundancji wynika tu ze zmniejszenia wielkości
, gdyż listy inwersyjne tworzymy dla mniejszej liczby deskryptorów.

du zupenego

---