ĆWICZENIE 10

WNIKANIE CIEPŁA OD ŚCIANKI DO POWIETRZA

1. Cel ćwiczenia.

Celem ćwiczenia jest wyznaczenie wartości współczynników wnikania ciepła dla konwekcji swobodnej w przestrzeni nieograniczonej i konwekcji swobodnej. Określa się także wpływ promieniowania cieplnego na wartość współczynnika wnikania ciepła dla konwekcji swobodnej oraz porównuje wartości wyznaczonych doświadczalnie i obliczonych teoretycznie współczynników wnikania ciepła dla konwekcji wymuszonej.

2. Schemat aparatury.

1- wentylator, 2 - zawór, 3 - zwężka, 4 - przewód powietrza, 5 - wymiennik, 6 - króciec wylotowy powietrza, 7 - termometry, 8 - przewód pary, 9 - wytwornica pary, 10 - przegroda, 11 - skraplacz nadmiaru pary, 12 - chłodnice kondensatu, 13 - zbiorniczki pomiarowe, 14 - zawory, 15 - latarki kontrolne, 16 - tablica elektryczna, 17 - manometr

3. Opracowanie wyników.

I. Konwekcja wymuszona (obliczenia dla pomiaru nr 1).

a) Obliczenie strumienia ciepła.

[W]

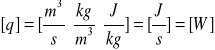
b) Obliczenie zastępczej różnicy temperatur.

[K]

[K]

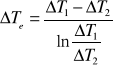
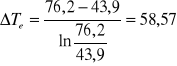
[K]

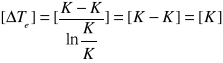
c) Obliczenie powierzchni wymiany ciepła.

[m²]

d) Obliczenie doświadczalnego współczynnika wnikania ciepła.

e) Obliczenie błędu bezwzględnego dla doświadczalnego współczynnika wnikania ciepła.

f) Obliczenie
oraz
.

=53,114 + 0,041=53,155

=53,114 - 0,041=53,073

g) Obliczenie liczby Nusselta.

[1]

h) Obliczenie liczby Reynoldsa.

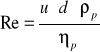
[1]

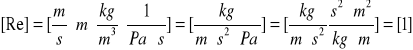
i) Wykres dwulogarytmiczny zależności Nu=f(Re).

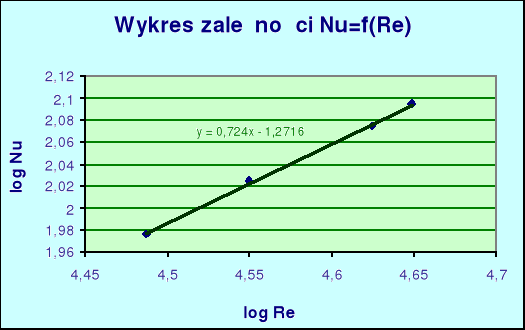
j) Wyznaczenie współczynników w równaniu.

Nu=

Przy wyznaczaniu współczynników zakładamy stałą wartość liczby Prandtla Pr oraz kryterium geometrycznego K_g. Dlatego też równanie przyjmuje postać:

Nu=

Korzystając z wykresu oraz równania wykreślonej funkcji możemy obliczyć współczynniki „W” oraz „Z”.

W=
0,2804

Z=0,724

Równanie przyjmuje postać:

Nu=0,2804Re^0,724

k) Obliczenie teoretycznego współczynnika wnikania ciepła.

Nu=

Nu=

Z równań tych otrzymujemy:

Liczba Prandtla wynosi:

Pr=0,722

II. Konwekcja swobodna.

a) Obliczenie strumienia ciepła.

[W]

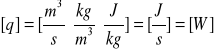
b) Obliczenie zastępczej różnicy temperatur.

[K]

[K]

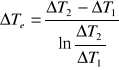
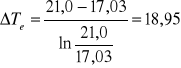
[K]

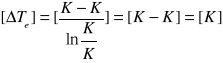
c) Obliczenie powierzchni wymiany ciepła.

[m²]

d) Obliczenie doświadczalnego współczynnika wnikania ciepła.

e) Obliczenie błędu bezwzględnego dla doświadczalnego współczynnika wnikania ciepła.

f) Obliczenie
oraz
.

=15,179 + 0,011=15,190

=15,179 - 0,011=15,168

g) Obliczenie wartości liczby Grashoffa.

Gr=

[

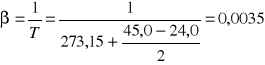
Gr=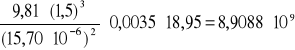
[1]

h) Obliczenie iloczynu liczb: Grashoffa i Prandtla.

Przyjmuję, że liczba Prandtla jest wielkością stałą i wynosi Pr=0,722.

Gr⋅Pr=8,9088⋅10⁹⋅0,722=6,4321⋅10⁹

2⋅10⁷<Gr⋅Pr<10¹³ więc Nu=0,135(Gr⋅Pr)^1/3

i) Obliczenie liczby Nusselta.

Nu=0,135(Gr⋅Pr)^1/3

Nu=
[1]

[Nu]=[1]

j) Obliczenie teoretycznego współczynnika wnikania ciepła.

k) Obliczenie temperatury powierzchni osłony izolacji wymiennika.

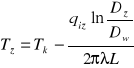
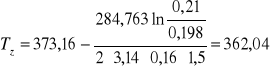
l) Porównanie temperatury izolacji zmierzonej i wyznaczonej teoretycznie.

T_{iz zm}=273,15+
[K]

T_{iz teor}=362,04 [K]

ł) Obliczenie strumienia ciepła przekazywanego od powierzchni osłony do otoczenia na drodze promieniowania.

[W]

m) Obliczenie wartości (doświadczalnego) współczynnika wnikania ciepła z równania bilansu.

[

4. Tabele podsumowujące.

Konwekcja wymuszona

Pomiar	Δp	uG	Temp. powietrza [^oC]		Czas napeł. zbiorniczka	Objętość zbiorniczka
nr	[mm H2O]	[m/s]	wlot	wylot	[s]	[cm^3]
1	48	12,04	23,80	56,1	173,73	60
2	66	13,92	23,70	55,4	154,35	60
3	88	15,64	22,97	54,1	139,25	60
4	105	16,52	23,07	53,3	131,70	60

Konwekcja swobodna

Pomiar	Temp. izolacji [^oC]		Temp. otocz.	Czas napeł. zbiorniczka	Objętość zbiorniczka
nr	1	2	[^oC]	[s]	[cm^3]
1	41,03	45,0	24,0	151,84	20

Wyniki obliczeń dla konwekcji wymuszonej.

Lp.	q1 [W]	ΔT1 [^oC]	ΔT2 [^oC]	ΔTe [K]	α1 [W/(m^2K)	Re	Nu	lg Re	lg Nu
1	746,648	76,20	43,9	58,57	53,114	30699,00	94,7442	4,487	1,977
2	840,396	76,30	44,6	59,04	59,311	35492,54	105,780	4,550	2,024
3	931,527	77,03	45,9	60,13	64,552	42110,76	118,618	4,624	2,074
4	984,929	76,93	46,7	60,56	67,762	44480,16	124,517	4,648	2,095

Równanie: Nu=0,2889Re^0,724

Wyniki obliczeń dla konwekcji swobodnej.

q2 [W]	Tz [K]	Gr	Pr	qp [W]	q2-qp [W]	α3 [W/(m^2K)]
284,763	362,04	8,9088⋅10^9	0,722	22,582	262,181	12,909

Ocena zgodności wartości doświadczalnych i teoretycznych.

Wartość	α1	Δα1	α1-Δα1	α1+Δα1	α2	Δα2	α2-Δα2	α2+Δα2
Doświadczalna	53,114	0,041	53,073	53,155	15,179	0,011	15,168	15,190
Teoretyczna	44,04	-	-	-	30,176	-	-	-
Zgodność +/-	-	-	-	-	-	-	-	-

Wartość	Tz	Δ Tz	Tz-ΔTz	Tz+ΔTz
Doświadczalna	316,17	0,1	316,07	316,27
Teoretyczna	362,04	0,1	361,94	362,14
Zgodność +/-	-	-	-	-

5. Wnioski.

Podczas przeprowadzania ćwiczenia można było zauważyć pewne prawidłowości. Przy pomiarach związanych z konwekcją wymuszoną (burzliwą- wskazują na to wartości liczby Reynoldsa) ze wzrostem prędkości przepływu powietrza malała jego temperatura na wylocie. Ponadto czas napełniania zbiorniczka kondensatu malał. Po dokonaniu obliczeń daje się zauważyć kolejne prawidłowości związane ze zmianą prędkości przepływu powietrza. Wraz ze wzrostem prędkości płynącego powietrza rósł współczynnik wnikania ciepła- zarówno doświadczalny jak i teoretyczny. Rosła także liczba Reynoldsa oraz Nusselta, a co za tym idzie ich logarytmy, co daję się zaobserwować na wykresie załączonym w sprawozdaniu. Niestety wartości doświadczalne różnią się dość znacznie od teoretycznych.

Podobną sytuacje możemy zaobserwować w przypadku konwekcji swobodnej. Tam także wszystkie wielkości wyznaczane doświadczalnie i teoretycznie odbiegały od siebie. Mogło to być spowodowane (w przypadku konwekcji swobodnej) dość dużą różnicą w temperaturze wymiennika obliczonej teoretycznie i wyznaczonej doświadczalnie. Różnica ta pociągnęła za sobą dalsze obliczenia, czego rezultatem są różnice w końcowych wynikach.

Porównując wyznaczone wielkości dla konwekcji wymuszonej i swobodnej możemy stwierdzić, iż zarówno strumienie ciepła, jak i wartości współczynników wnikania ciepła są znacznie wyższe dla konwekcji wymuszonej.

6. Dyskusja błędów.

Podczas ćwiczenia mogły zostać popełnione pewne błędy, które mogły wpłynąć na otrzymane wyniki. Główny błąd był związany z pomiarem czasu napełniania zbiorniczków kondensatem- błąd paralaksy podczas odczytywania objętości ze zbiorniczka oraz błąd związany z opóźnieniem reakcji podczas posługiwania się stoperem. Ponadto niewielki wpływ na końcowe wyniki mógł mieć fakt odczytywania temperatury tylko z pewna dokładnością oraz przybliżenia stosowane podczas obliczeń w wykonywanym sprawozdaniu.

---