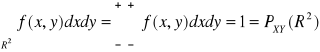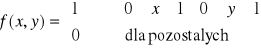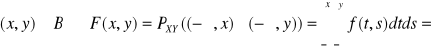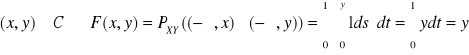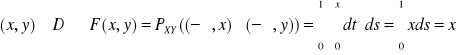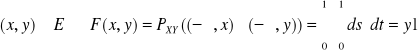ZMIENNE LOSOWE WIELOWYMIAROWE

,

Def:
nazywamy n-wymiarową zmienna losową (wektorem losowym).
.
.

Def: Jeżeli zmienna losowa X przyjmuje co najwyżej przeliczalną liczbę wartości
to mówimy, że zmienna losowa X ma rozkład dyskretny:
,
.

Def: X ma rozkład ciągły jeżeli istnieje sumowalna i nieujemna funkcja
taka, że
, gdzie
- miara Lebesque'a na
.

Np1.: (n=2) Z tali 52 kart wybrano 1 kartę. Zmienna losowa X przyjmuje wartości: 1 jeżeli wylosowana karta jest asem, 0 - jeżeli nie jest asem. Zmienna losowa Y: 1 jeżeli jest pikiem, 0 - jeżeli nie jest. Wyznaczyć rozkład (X,Y).

X

Y

0

1

0

1

Def: W przestrzeni
przyjmujemy następujący porządek: Jeżeli
,
, to mówimy, że
.

Def:
- zmienna losowa

nazywamy dystrybuantą n-wymiarowej zmiennej losowej.

dla n=2

Tw: Jeżeli
- dwuwymiarowa zmienna losowa, to
spełnia następujące warunki:

1. 
   

2. 
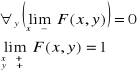
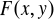
   jest funkcją niemalejącą ze względu na każda ze zmiennych z osobna
   przy ustalonej drugiej zmiennej.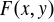

3. 
   jest funkcją lewostronnie ciągłą ze względu na każda ze zmiennych z
   osobna przy ustalonej drugiej zmiennej.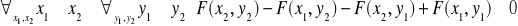

4. 
   

(dodatnie pole prostokąta)

Tw: Jeżeli
spełnia warunki 1º-4º, to funkcja ta jest dystrybuantą rozkładu pewnej zmiennej losowej i ten rozkład jest wyznaczony jednoznacznie.

Tw: Jeżeli rozkład zmiennej losowej
jest ciągły (
), to wówczas
w każdym punkcie ciągłości
.

Np1. (ciąg dalszy) Szukamy dystrybuanty:

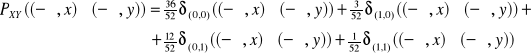
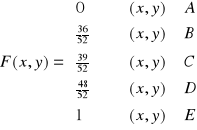
Def:
⇔

Tw:
ma rozkład ciągły, tzn.
, gdzie

jest sumowalna i nieujemna

Aby
była gęstością pewnej zmiennej losowej
:

1. 
   

2. 
   

Np2.:

ma rozkład jednostajny w prostokącie P

1. 
   

2. 
   

3. 
   

4. 
   

5. 
   




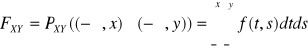
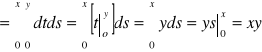
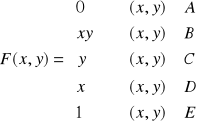
Tw: Jeżeli
ma rozkład dyskretny
, to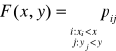
.

Tw: Jeżeli
ma rozkład ciągły
, to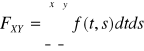
.

Rozkłady brzegowe:


n-wymiarowa zmienna losowa


zmienna losowa

Def: Rozkład zmiennej
nazywamy i-tym rozkładem brzegowym w
n-wymiarowym rozkładzie zmiennej X.

I.
ma rozkład dyskretny






Oznaczenia:














Def:
jest rozkładem brzegowym zmiennej X w dwuwymiarowym rozkładzie zmiennej
.


jest rozkładem brzegowym zmiennej Y w dwuwymiarowym rozkładzie zmiennej


np1: (c.d.)

X

Y

0

1




0










1






















5

Luke Rachunek prawdopodobieństwa-wykład 14.5.2k+1

#

---