§5 Pochodna Funkcji Rzeczywistej Zmiennej Rzeczywistej

Niech f: (a,b)→R oraz x₀∈(a,b). To dla x₁ ∈(a,b) przyrostem zmiennej niezależnej w x₀ nazywamy różnicę ∆x=x₁-x₀, a przyrostem zmiennej zależnej w x₀ nazywamy różnicę ∆y=f(x₁)-x₀. Iloczynem różnicowym f funkcji w przedziale x₀ nazywamy iloraz postaci

Jeżeli przy ∆x=0 istnieje granica właściwa (skończona) lub niewłaściwa (+∞,-∞) ilorazu różnicowego
funkcji f w x₀, to punktowi x₀ można przyporządkować wyrażenie
. Zmieniając x₀∈(a,b) uzyskujemy funkcję f ' , która przyporządkowuje zmiennej x wyrażenie:

Funkcja f ' jest określona w tych punktach przedziału (a, b) w których istnieje granica (1)

Definicja:

Funkcję f ' , gdzie

Nazywamy pochodną funkcji f

We wzorze (1) można rozważać granicę prawo-lewostronną

Definicja:

Pochodną prawostronną funkcji f nazywamy funkcję f 'p, przy czym

Pochodną lewostronną funkcji f nazywamy funkcję f 'l, przy czym

Jeżeli istnieje skończona pochodna funkcji f w punkcie x₀∈(a,b). to w tym punkcie istnieją skończone i równe sobie obie pochodne jednostronne funkcji f. Na odwrót z istnienia skończonych i równych sobie pochodnych jednostronnych funkcji f w x wynika istnienie skończonej pochodnej f '(x₀)

Przykłady:

1. Wykazać, że:(xⁿ)=nx^n-1 dla n=1,2,3....

Dowód oznaczamy przez ∆x przyrost zmiennej niezależnej x wtedy ∆y=f(x+∆x)-f(x)=(x+∆x)ⁿ-xⁿ f(x)=x^''

Stosując wzór dwumianowy NEWTONA

,

otrzymujemy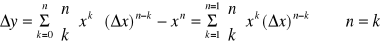

ponadto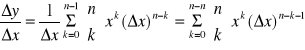
,

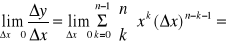
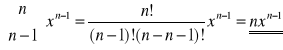
Wykazany wzór zachodzi dla n>1, oraz dla każdego x∈R a przy n=1 dla x≠0. Dla n=1 oraz x=0 powyższy wzór traci sens liniowy, gdyż otrzymujemy:

Wyrażenie nieoznaczone typu (0⁰)

2. Zbadać pochodną funkcji

f(x)=x w punkcie x₀=0

Rozwiązanie: Pochodne jednostronne funkcji f w x₀=0 wynoszą:

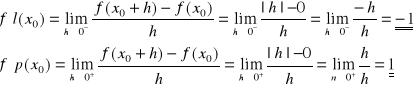
Pochodne są różne, zatem: f'l(x₀)≠f'p(x₀), czyli funkcja f(x)=x, mimo, że jest ciągła w x₀=0 nie posiada pochodnej w tym punkcie.

Twierdzenie 1

Jeżeli funkcja f określona na przedziale (a, b) posiada skończoną pochodną w punkcie x₀∈(a,b), to f jest ciągła w x₀.

Dowód:

Jeżeli istnieje skończona pochodna
, to
,

czyli
, tzn. f jest ciągła w x₀

Twierdzenie odwrotne do twierdzenia 1 jest nieprawdziwe, gdyż np. funkcja ciągła f(x)=x nie posiada pochodnej w x₀=0.

Twierdzenie 2

Jeżeli funkcje f, oraz g posiadają skończoną pochodną w punkcie x₀, to:

a.)funkcja α·f+β·g, , gdzie α,β - stałe rzeczywiste, posiada skończoną pochodną w x₀, oraz [αf+βg]'=(x₀)= α·f'(x₀)+ β·g'(x₀)

b.)iloczyn f·g posiada skończoną pochodną w x₀, oraz (f·g)'(x₀)= f'(x₀)·g(x₀)+ f(x₀)·g'(x₀)c.)przy dodatkowym założeniu g(x₀)≠0 istnieje skończona pochodna ilorazu f/g, oraz pochodna ta wynosi

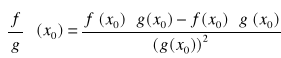
a.) (αf+βg)'(x₀)=αf'(x₀)+βg'(x₀)

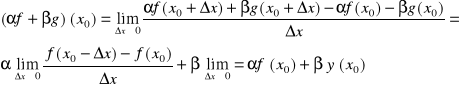
b.) (f·g)'(x₀)= f'(x₀)·g(x₀)+ f(x₀)·g'(x₀)

Dowód:

b.)

gdyż g jest ciągła w x₀

c.)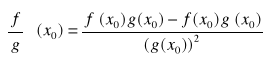

Dowód:

Ponieważ g(x₀)≠0, oraz istnieje skończona pochodna g'(x₀), czyli g jest ciągła w x₀, więc dla dostatecznie małych w do bezwzględnej wartości ∆x, mamy g(x₀+∆x)≠0, zatem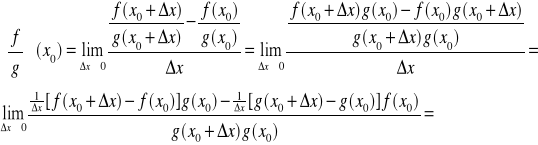

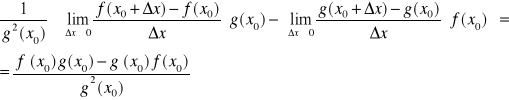
Twierdzenie 3 Jeżeli funkcja g jest określona na przedziale domkniętym <a, b>, oraz istnieje skończona pochodna g(x₀) dla pewnego x₀∈(a,b) funkcja f jest określana na przedziale <0,α>⊃g(<a,b>0) - przeciwdziedzina funkcji g, f ma skończoną pochodną w punkcie g(x₀)∈(c,d), to h'(x₀)=(f∙g)'(x₀)=f'(g(x₀), gdzie h - superpozycja funkcji f, g

Dowód:

Ponieważ istnieją skończone pochodne g'(x₀), f'(y₀), gdzie y=g(x₀), więc przyjmując, że ∆y=g(x₀+∆x)-g(x₀), otrzymujemy g(x₀+∆x)-g(x₀)=∆x[g'(x₀)+v(x₀,∆x)], f(y₀+∆y)-f(y₀)=∆y[f'(x₀)+v(y₀,∆y)],

Gdzie v(x₀,∆x)]→0 przy ∆x→0 i v(y₀,∆y)]→0 przy ∆y→0, zatem: h(x₀+∆x)-h(x₀)=f[g(x₀+∆x)-f[g(x₀)]=f[g(x₀)], =f[g(x₀)+∆y]-f[g(x₀)]=[g(x₀+∆x)-g(x₀)][f'(y₀)+ v(y₀,∆y)]= ∆x[g'(x₀)+h(x₀,∆x)][f'(y₀)+ v(y₀,∆y)] a więc:

Twierdzenie 4

Jeżeli funkcja jest ściśle monotoniczna na przedziale (a,b), oraz istnieje skończona pochodna f'(x₀)≠0 w punkcie x₀∈(a,b) to funkcja odwrotna do f:f₁ posiada pochodną w punkcie y₀=f(x₀), przy czym

Pochodną funkcji f gdzie y=f(x) w punkcie x₀ oznaczamy również symbolem

Pochodne funkcji elementarnych

f(x)=x^α, gdzie α∈ℜ

Dla x₀≠0 kolejno otrzymujemy:

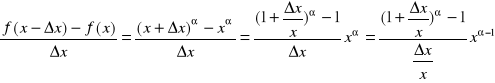
Wiemy, że

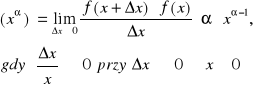
Jeżeli x=0 to zakładamy, że α>0 wtedy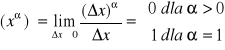

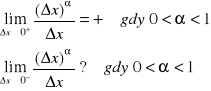
b.) f(x)=sinx Ponieważ

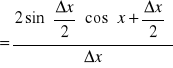
Więc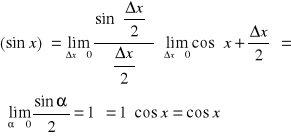

f(x)=cosx

Korzystamy z tw. o pochodnej funkcji złożonej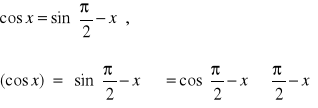

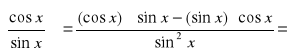
c.) f(x)=arcsinx

Funkcją odwrotną do g=arcsinx jest funkcja x=siny dla

Z tw.4 wynika, że x'(y)=cosy oraz
.

Ponieważ
(znak + przed pierwiastkiem)

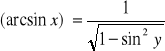
x∈(-1,1)

Podobnie otrzymujemy
x∈(-1,1)

f(x)=arctgx Funkcją odwrotną do funkcji y=arctgx jest funkcja x=tgy dla
Ponadto

Ze względu na to, że
pochodna x'(y) zawsze istnieje jest różna od zera, z tw.4 otrzymujemy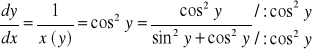

Analogicznie otrzymujemy

d.) f(x)=log_ax, a>0, a≠0, x>0

Ponieważ iloraz różnicowy dla funkcji log ma postać:

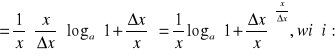
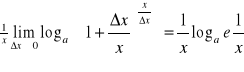
w szczególności

e.) f(x)=a^x, a>0, x∈R

Ponieważ funkcją odwrotną do funkcji wykładniczej

Y=a^x, a>0, a≠1 jest funkcja logarytmiczna x=log_ay, więc korzystając z tw.4 otrzymujemy:

, oraz
,

czyli (a^x)'=a^xlna w szczególności (e^x)'=e^x Jeżeli a=1 f(x)=1^x oraz f'(x)=0 Interpretacja geometryczna i mechaniczna pochodnej. Zakładamy, że funkcja f jest określona na przedziale (a, b), oraz istnieje skończona pochodna f'(x₀) w punkcie x₀∈(a,b). Równanie prostej przechodzącej przez punkty P₀=P₀(x₀,f(x₀)),P₁(x₁f(x₁)) ma postać
. Przy x₁→x₀, tzn., gdy ∆x→0 sieczna P₀,P₁ krzywej y=f(x) dąży do położenia granicznego, którym jest styczna do krzywej y=f(x) w punkcie P₀.. Podobnie jest, gdy ∆x<0. Wtedy, tzn. przy x₁→x₀ współczynnik kierunkowy siecznej, tzn.

dąży do pochodnej funkcji f w

punkcie x₀ i f'(x₀). Zatem jeżeli funkcja f posiada skończoną pochodną w punkcie x₀, to równanie stycznej do krzywej y=f(x) w punkcie (x₀,f(x₀)) ma postać y-f(x₀)=f'(x₀)(x-x₀), tzn. współczynnik kierunkowy stycznej jest równy f'(x₀).

b.) Niech dane ciało porusza się po osi liczbowej OX

W chwili t, ciało znajduje się w punkcie M₀ współrzędnej w chwili początkowej ciało znajduje się w punkcie M₀ o współrzędnej s₀=f(t₀). Po upływie czasu ∆t ciało znajduje się w punkcie M₁=M₁(S₁), gdzie S₁=f(t₀+∆t). Oznaczamy ∆s=s₁-s₀. Prędkość średnią ciała na odcinku M₀, M₁, nazywamy ilorazem
.

Graniczną wartość prędkości średniej, czyli
, nazywamy prędkością ciała w chwili t₀ i oznaczamy przez
. Przy założeniu istnienia skończonej granicy. Zatem
przy założeniu istnienia skończonej pochodnej f'(t₀).

c.) Badamy funkcję syntezy substancji C z substancji A, oraz B. Ilość g substancji C zależy od czasu t trwania reakcji w następujący sposób:y=f(t). W chwili t₀, ilość substancji C wynosi y₀=f(x₀). Po upływie czasu ∆t, ilość substancji C wynosi y₁=f(t₀+∆t)

Nazywamy prędkością średnią reakcji w czasie w chwili t₀, do chwili
. Prędkością reakcji w chwili t₀, nazywamy granicę
, przy założeniu istnienia skończonej pochodnej f(t₀). Pochodna funkcji przedstawionej parametrycznie.

Dane są dwie funkcje x=p(t), y=f(t) określone i ciągłe względem parametru +G<α,β> określające związek zmiennych y, oraz x przy pomocy parametru t.

Zakładamy, że:

1. f jest ściśle monotoniczna na przedziale <α,β>

2. istnieją skończone pochodne:

f'(t₀)≠0 f'(t₀) w punkcie t₀∈(α,β), a zatem istnieje funkcja odwrotna f_-1, która jest ciągła i ściśle monotoniczna. Funkcja złożona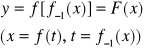
, która jest ciągła

Z tw. o pochodnej funkcji odwrotnej otrzymujemy
, gdzie x₀=f(t₀). Z twierdzenia o pochodnej funkcji złożonej wynika, że: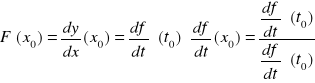
,

czyli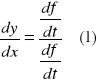
.

Przykład:Niech

Wykresem powyższej funkcji jest półokrąg nieujemny o promieniu t. Ponieważ

1. funkcja f jest malejąca na przedziale <0,π>

b.)

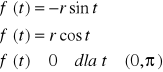
więc na mocy (1) otrzymujemy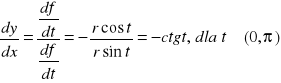
.

§6 POCHODNE WYŻSZYCH RZĘDÓW

DEFINICJA:Niech funkcja f posiada skończoną pochodną f' na przedziale (a;b). Pochodną II rzędu lub drugą pochodną funkcji f nazywamy pochodną funkcji f przy założeniu, że pochodna ta istnieje. Oznaczamy ją symbolem f^II lub f⁽²⁾.

Ogólnie zakładamy, że istnieje skończona pochodna (n-1)-go rzędu lub (n-1)-a pochodna f^(n-1)Pochodną n-tego rzędu lub n-tą pochodną funkcji f nazywamy pochodną funkcji f^(n-1), przy założeniu, że pochodna ta istnieje.Kolejne pochodne funkcji f oznaczmy następująco:

.

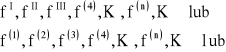
Ogólnie:

dla

Przy obliczeniu pochodnej n-tego rzędu iloczynu dwóch funkcji, korzystamy ze wzoru Leibniza:Jeżeli funkcje f, g posiadają skończone pochodne do n rzędu włącznie w otoczeniu punktu x₀∈(a,b), to:

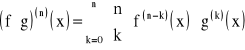
przy
, dla x z powyższego otoczenia x₀.

§7 RÓŻNICZKA

DEFINICJA:Niech funkcja f będzie określona na przedziale (a;b). Przyrostowi Δx zmiennej niezależnej odpowiada przyrost zmiennej zależnej w punkcie x₀∈(a,b):∆y=f(x₀+∆x)-f(x₀)

Mówimy, że funkcja f jest różniczkowalna w punkcie x₀, jeżeli jej przyrost w x₀ można zapisać w postaci: ∆y=A∆x+o(∆x), gdzie A jest stałą,
,
.

TWIERDZENIE 1:

Na to, by funkcja była różniczkowalna w punkcie x₀∈(a,b) potrzeba i wystarcza, by istniała skończona pochodna f'(x₀). Jeżeli warunek ten zachodzi to przyrost funkcji f w punkcie x₀ ma postać: f(x₀+∆x)-f(x₀)=f'(x₀)∆x+o(∆x)

, gdzie
.

UWAGA!

W przypadku, gdy x₀ leży na jednym z krańców przedziału <a,b> rozważamy przyrost i pochodne jednostronne.

DOWÓD:Konieczność:

Zakładamy, że funkcja f jest różniczkowalna w x₀∈(a,b), tzn.

∆y=f(x₀+∆x)-f(x₀)=A∆x+o(∆x).

Zatem przy ∆≠0 otrzymujemy:

.Przechodząc do granicy mamy równość:

,

czyli: A=f'(x₀)

f(x₀+∆x)-f(x₀)=f'(x₀)∆x+o(∆x).

Dostateczność:

Jeżeli funkcja f posiada w x₀ skończoną pochodną f'(x₀), to
przy ∆x→0 Oznaczmy:

. (1)

Wtedy: α→0 przy ∆x→0.

Ponadto z (1) wynika, że:

,

gdyż:

Definicja: Niech funkcja f będzie określona na przedziale (a,b) oraz istnieje skończona pochodna f^|(x) dla każdego xε(a,b). Różniczkę funkcji f ze względu na przyrost h nazywamy funkcją dt=f^|*h Wartość różniczki funkcji f w punkcie x₀ε(a,b) wynosi dt(x₀)=f^|(x₀)*h. Podstawiając f(x)=x, otrzymujemy f^|(x)=1 oraz dt=dx=1*h, a stąd df(x)=f^|(x)dx dla xε(a,b). Ponieważ dla funkcji różniczkowalnej f w x₀ε(a,b) mamy Δt(x₀)=f(x₀+Δx)-fx₀=f^|(x₀)Δx+(Δx) Więc przy Δx bliskich zero, tzn dla małych |Δx|, przyrost funkcji f w x₀: Δf(x₀)=f^|(x₀)*Δx tzn Δf(x₀)≈dt(x₀) (równość przybliżona).Korzyści wynikające z zamiany przyrostu Δf(x₀) na różniczkę df(x₀) polega na tym, że df(x₀) zależy od przyrostu Δx liniowa. Podstawmy Δx=x-x₀, czyli x=x₀+Δx wtedy f(x)-f(x₀)≈f^|(x₀)(x-x₀) oraz f(x)≈f(x₀)+f^|(x₀)(x-x₀) dla bliskich x₀. W szczególności dla x₀=0 mamy f(x)≈f(0)+f^|(0)*x dla x bliskich zeru. Zakładamy, że istnieje skończona pochodna f'(x₀). ∆x=x₁-x_0, ∆y=f(x₁)-f(x₀)Jeżeli zastąpimy krzywą y=f(x), styczną do tej krzywej w punkcie P₀, to przyrost zmiennej zależnej dla punktów stycznej wynosi:df=f'(x₀)∆x

df=f'(x₀)dx. Dla małych co do bezwzględnej wartości ∆x przyrost funkcji f możemy w przybliżeniu zastąpić jej różniczką:

∆y=f(x_o+∆x)-f(x₀)≈f'(x₀)∆x.

---