1. Rodzaje oddziaływań w przyrodzie:
1)oddziaływania grawitacyjne m>0
2)słabe jądrowe 10¯¹⁵m, 1A°=10⁻¹⁰
enksztrent czyli rozmiar jądra
3)tarcie elektromagnetyczne
(g>0 g<0) ład. +i-
4)silnie jądrowe
2.Zasada zachowania energii:
Praca - jest to iloczyn skalarny siły i przesunięcia.
(W=
°
=Fs cos(

)
Energia kinetyczna-(ciało w ruchu)
jest to różnica pomiędzy energią całkowitą ciała a energia spoczynkową
(kwadrat)
Energia potencjalna-energia zmagazynowana do użycia w przyszłości lub jest to zdolność do wykonania pracy lub na podstawie twierdzenia o pracy i energii do zwiększenia energii kinetycznej ciała.
Ep(
)=
(w)·ds.(w)
Siła oddziaływania jest równa grad enerii potencjalnej
=- gradEp
3.Zasada zachowania pędu:
Pęd zależy od masy i prędkości:

=M
s


Mat. Zapis zasady zachowania p.

=0→
= const
Kiedy suma sił zewn.działających na układ cząstek wynosi 0 to całkowity pęd układu pozostaje stały.
4.Zasada zachowania momentu pędu:

zew=
(
)
Kiedy wypadkowy moment sił zewnętrznych działających na układ wynosi 0 całkowity moment pędu układu pozostaje stały.
wzór:
=
x

L(w)-moment pędu punktu materialnego,r(w)-wektor łączący punkt , p(w)-pęd punktu materialnego

5a. Ruch harmoniczny prosty-jeżeli ciało drga dookoła położenia równowagi pod wpływem siły , która jest proporcjonalna do jej odległości i położenia równowagi to mówimy ż ciało wykonuje ruch drgający prosty (zawsze siła w ruchu drgającym jest proporcjonalna do wychylenia i odwrotnie do niego skierowana

5b Ruch harmoniczny tłumiony- Jeżeli drgania ciała odbywają się w ośrodku materialnym ,to wskutek występowania siły oporu ośrodka ,drgania będą zanikać .Niezależnie od natury ośrodka siła tłumiąca F_t,jest proporcjonalna do prędkości ciała drgającego, jeżeli ta prędkość jest niewielka.

F_t= -b^dx

5c. Ruch harmoniczny wymuszony - rezonans.

Bardzo ważnym przypadkiem jest przypadek ruchu punktu , który może drgać ruchem harmonicznym gdy działa nań siła periodyczna zewnętrzna

Gdy pobudzamy układ do drgań siłą zewnętrzną, która zmienia się z częstotliwością
, to STWIERDZAMY:

I. Nie występuje tłumienie drgań, ponieważ doprowadzona z zewnątrz energia równoważy straty energii na pokonanie oporów ruchu.

II. Układ zaczyna drgać z często-tliwością
.

III. Amplituda drgań zależy od częstotliwości

Równanie ruchu drgającego wymuszonego:

AMPLITUDA RUCHU WYMUSZONEGO:

Jeśli amplituda drgań będzie maksymalna to wtedy zachodzi zjawisko

REZONANSU.(Rezonans występuje wtedy gdy jest brak tłumienia).

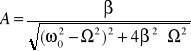
aby obliczyc Amplitudę max musimy wziąć pochodne i przyrównując do zera

-częstotliwość drgań układu

Im stała β jest mniejsza tym ostrzejsza jest krzywa rezonansu, tzn. tym ostrzej jest określona częstotliwość rezonansu
przy której amplituda osiąga maksimum.

SKUTKI REZONANSU:

a)gdy częstotliwość zbliża się częstotliwości rezonansowej amplituda rośnie,

b)wzrost amplitudy powoduje wzrost przyspieszenia i prędkości,

c)w przypadku ciała ludzkiego rezultatem drgań o zbyt dużej amplitudzie jest ból,

d)w ogólności drgania mogą spowodować uszkodzenia, mogą wyzwolić naprężenia zamrożone w danej strukturze, tak więc drgania budynku powodują osiadania ziemi co prowadzi do przesuwania się fundamentów.

6.Interferencja fal sprężystych. Jeżeli do dowolnego punktu ośrodka dociera w tym samym momencie kilka ciągów fal to punkt ten doznaje wychylenia będącego siłą poszczególnych wychyleń wywołanych przez dochodzenie do punktu ciągu fal.Jest to tzw. zasada niezakłóconej superpozycji.

W myśl tej zasady każdy ciąg fal rozchodzi się tak w przestrzeni jak gdyby nie było innych ciągów fal. Wszystkie zjawiska które są wywołane przez zakłócone nakład nie się fal nazywamy krótko interferencja fal.

9 Ciepło właściwe gazów doskon ałych. nazywamy ilość ciepła, którą musi wymienić z otoczeniem 1 mol gazu ,aby zmienić swą temperaturę o 1K.

Gaz doskonały (gaz idealny dla którego wszystkie równania są proste).

Gaz doskonały definiuje się następująco: a) cząsteczki gazu poruszają się chaotycznie we wszystkich kierunkach, z których żaden nie jest uprzywilejowany, b) cząsteczki zderzają się sprężyście ze sobą wzajemnie i ze ściankami naczynia, w którym znajduje się gaz; c) między cząsteczkami nie działają żadne siły, poza krótką chwilą, w której następuje zderzenie, d) cząsteczki poruszają się od zderzenia do zderzenia ruchem jednostajnym prostoliniowym, e) suma objętości cząsteczek gazu jest dużo mniejsza od objętości naczynia, w którym znajduj się gaz.

Równanie stanu gazu doskonałego (równanie Clapeyrona)

pV=nRT

p - ciśnienie gazu doskonałego, V - objętość gazu doskonałego, n - liczba moli, R - stała gazowa, T - temp. gazu doskonałego.

Cechy gazu doskonałego:

a) gaz składa się z molekuł. Molekuły mogą być jedno lub wieloatomowe, b) molekuły znajdują się w ciągłym ruchu i podlegają Newtonowskim zasadom ruchu, tzn. molekuły poruszają się z różnymi prędkościami i w różnych kierunkach, c) całkowita liczba cząsteczek jest olbrzymia, kierunki i prędkości molekuł mogą się gwałtownie zmieniać w wyniku zderzeń ze ściankami naczynia ł innymi molekułami, d) objętości samych molekuł są bardzo małe w porównaniu z objętością zajmowaną przez gaz, e) między molekułami nie działają żadne siły (nie ma oddziaływań w tym gazie), f) zderzenia molekuł są doskonale sprężyste i czas tych zderzeń jest bardzo krótki.

C_V - ciepło właściwe mierzone przy stałej objętości.

C_P - ciepło właściwe mierzono przy stałym ciśnieniu.

C_V=C_P-R

C_P =C_V+R

10.Przemiany stanu gazów dosko nałych. Przemiana izotermiczna. zachodzi w stałej temperaturze. W tej przemianie zmiana energii wewnętrznej jest równa zeru, gdyż temp. gazu nie zmienia się. Gdy gaz pobiera ciepło, to jest ono całe zużyte na wykonanie przez gaz pracy. W tej przemianie T = const.Z równania Clapeyrona wyznaczamy

p = ^nRT

I otrzymujemy

W = -nRT ∫^dV =nRT ln ^V

Przemiana izobaryczna . zachodzi przy starym ciśnieniu. W czasie tej przemiany gaz pobiera ciepło i wykonuje pracę,p = const. Pracę możemy zatem obl. W = - p ∫ dV = p (V₁ - V₂)

Przemiana izochoryczna W tej przem ianie V = const. Zatem V₁ = V₂ i praca sił ciśnienia jest równa 0 Przemiana adiabatyczna nazywamy Przemianę zachodzącą bez wymiany Ciepła z otoczeniem.

W przemianie tej praca wykonywana przez układ równa jest ubytkowi energii wewnętrznej układu, a więc dW=-dU.

PV^χ=const - równanie Poissona.

Stosując I zasadę Termodynamiki do 1 mola gazu doskonałego w przypadku przemiany adiaba tycznej można zapisać C_vdT = ­­-pdV

Równanie Clapeyrona Jest to niewątpliwie odmiana równania stanu gazu doskonałego wiążąca ze sobą tak łatwo dostępne do mierzenia wielkości fizyczne, jak masa gazu, jego masa cząsteczkowa oraz parametry określające stan fizyczny gazu.

pV = ^m RT

11.równanie gazów rzeczywistych(Van der valsa), równanie postaci:(p + a/V²)( V-b)= RT ,gdzie: a, b - stałe charakterystyczne dla gazu, wyznaczane empirycznie na podstawie zależności : a=27R²T_kr2/64p_kr, b=RT_kr/8p_kr, gdzie: T_kr, p_kr - temperatura i ciśnienie gazu w stanie krytycznym, V - objętość gazu, n - liczba moli gazu, R - stała gazowa, temperatura bezwzględna Równanie stanu gazó w rzeczywistych daje lepsze przyb liżenie rzeczywistej izotermy p(V) aniżeli równanie stanu gazów doskonałych , uwzględnia ponadto zjawisko skroplenia gazów i zjawiska krytyczne.

7,8,12a. Zasady termodynamiki

0 Jeżeli każde z 2 ciał A i B jest w równowadze termicznej z 3 ciałem C ( termometrem ) to A i B są w równowadze termicznej ze sobą

1.ciepło dostarczone układowi zostaje zużyte na zwiększenie energii wewnętrznej ukł i na wykonanie przez ukł pracy przeciwko siła zewnętrznym

dU=dQ+dW

2 Silnik cieplny działający periodycznie i nie zasilany żadną inną formą energii musi pobierać ciepło ze źródła o temp. wyższej od najzimniejszego ciała otoczenia.(silnik periodyczny- wykonuje zamknięty cykl przemian)

W=Q₁+

12b Cykl Carnota. Procesem kołowym albo cyklem nazywamy taki proces, w wyniku którego układ termodynamiczny powraca do stanu wyjściowego. Przykładem procesu kołowego jest cykl Carnota. Składa się on z dwóch izotermicznych i dwu adiabatycznych.

Jest to cykl wyidealizowany w którym wszystkie przemiany są odwracalne.

Praca wykonana przez gaz w cyklu Carnota: W=nR(T₁-T2)ln V₂/V₁

16 Pole grawitacyjne- 2 dowlone ciała materialne przyciągają się w kierunku lączącej je prostej proporcjonalnej sił proporcjonalną do iloczynu ich mas a dowrotnie proporcjonalną do kwadratu odległości tych ciał

F=G*

Pole grawitacyjne jest przykładem pola wektorowego.

g- wektor natężenia pola gr'agitacyjnego.

Pole grawitacyjne jest: a) polem wektorowym, b) polem zachowawczym,

c) polem stacjonarnym.

17. Prawo Gausa dla pola elektrycznego informuje że źródło pola elektrycznego są ładunki elektryczne q o gęstości ładunku p. Prawo Culomba Dwa nieruchome punktowe ładunki elektryczne oddziałujące między sobą siłami wprost proporcjonalnymi do iloczynu wartości tych ładunków i odwrotnie proporcjonalna do kwadratu odległości między nimi.

19.Polaryzacja dielektryków po umieszczeniu w polu elektrycznym dielektryku tym powstaje różne od zera pole elektryczne. Pole to działa pewną siłą na ładunki elektryczne znajdujące się wewnątrz dielektryka ,wskutek czego ładunki dodatnie przesuwają się w kierunku działania pola , a ładunki ujemne w kierunku przeciwnym .

21. Indukcja elektromagnetyczne Wytwarzanie prądu w wyniku zmian pola magnetycznego nazywamy indukcją elektro magnetyczną. Prawo indukcji magnetycznej (Faraday). d Ø B

[V] E - dt

22 Drgania elektromagnetyczne. Ruch bez tłumienia F= - kx z II z. dynamiki

d²x

m= dt +kx= 0

x = A cos (ωt +ϕ)

dx

dt = - w A sin (ωt + ϕ)

d²x

dt = - w² A cos (ω t + ϕ)

21. Równania Maxwella-

I jest prawem gausa dla pola elektrycznego i mówi o tym że źródłem pola elektrycznego jest ładunek elektryczny Q(rozłożony z wielkością ƍ)

Różniczkowe

E(w)=

II jest prawem Gausa dla pola magnetycznego pokazuje pole bezźródłowe

Skalarnie

divB(w)=0

III jest uwarunkowaniem prawa Faradaya , wynika z niego że chcąc wytworzyć pole elektryczne nie musi istnieć przewodnik z prądem wystraczy że istnieje zmienne w czasie pole elektryczne B

Rot E(w)= -

IV jest uwarunkowaniem prawa Ampera i zakłada że wirowe pole elektryczne powstaje w Okół przewodnika z prądem przewodzenia czyliw wyniku ruchu ładunku oraz że pole magnetyczne powstaje w wyniku istnienia zmiennego w czasie pola elektrycznego E

22 Powstawanie fal elektromagnetyczne Widmo fal elektromagnetyczne.. Źródłem fal elektromagnetycznych jest drgający dipol. Ciąg na prze mian powstających pól elektrycznych i magnetycznych nazywa się falą elekt romagnetyczna.2

23. . Podstawowe prawa optyki geometrycznej.

I Odbicie światła

II Promień padający odbity i normalna do powierzchni odbijającej leży w jednej płaszczyźnie. Jeśli światło przechodzi z jednegoośrodka do drugiego to światło się załamuje.

I prawo załamania

Sin n₂

sin = n₁ = N_{2 1}

II promień padający załamany i normalnaDo powierzchni leży na jednej płaszczyźnie.Współ czynnik załamania bezwględny

c

n_b= >1

25a. Interferencje światła Jeżeli do jakiegoś punktu ośrodka docierają równocześnie dwie wiązki fal świetlnych wówczas podobnie jak w przypadku fal sprężystych fale to wagą że sobą interferować. Warunkiem interferencji jest koherętność (spójność) spotykających się wiązek światła. Dwie wiązki są spójne jeżeli różnią się w fazie O staławielkość przynajmniej przez czas odpowiadający większej ilości okresu.

y=A cos (ω t -kx)

24.Zjawisko dyspersji światła zależy od

V = f(λ ) ,n = f(λ), =λ , = λ ,

czerwone

fiolet

>0 dyspersja normalna

<0 dyspersja anomalna

=0 dyspersja nie występuje

Prędkość fali świetlnej przechodzą cej przez ośrodek materialny zależy od współczynnika załamania tego ośrodka oraz od częstotliwości drgań przechodzącej fali. Ze wzrostem częstotliwości fali świetlnej rośnie współczynnik załamania ośrodka, a więc ze wzrostem częstotliwości fali malej e jej prędkości. Zjawisko to wykorzystujemy w spektrometrii promieniowania świetlnego. Spektrometrem jest pryzmat.

25b.Zjawisko dyfrakcji światła , polegające na uginaniu się promieni świetlnych napotykających na swej drodze przeszkody, w wyniku czego występują odstępstwa od prosto liniowego ich biegu,jest śćiśle związane z falową naturą światła .Śiatką dyfrakcyjną nazywamy zbiór dużej liczby jednakowych, równoległych szczelin, między którymi występują równe odstępy

26.Prawo Archimedesa- na każde ciało zanurzone w płynie , działa siła wypadkowa , która jest skierowana ku górze i równa ciężarowi wywartemu przez to ciało

F wyporu =ƍ*g*V wyporu

27. Równanie Bernoulliego- w czasie przepływu cieczy , suma ciśnienia statycznego i dynamicznego jest stała wzdłuż każdej linii przepływu.

P+pgh+
p
=const

Pierwsze dwa człony możemy ująć ogólną nazwą; ciśnienie statyczne

Natomiast trzeci człon to ciśnienie dynamiczne

pv kwadrat ….

---