Zadania przygotowawcze do drugiego kolokwium*

*Podstawą sukcesywnego zaliczenia kolokwium jest samodzielne przeprowadzenie obliczeń dla podanych zadań i przykładów.

WARUNKI BRZEGOWE

Zad. 1.

Dane są dwa ośrodki:

1. ε_w=2 dla y < 0

2. ε_w=9 dla y > 0

Gęstość ładunku powierzchniowego w płaszczyźnie y = 0 wynosi ρ_s. Mając dany w płaszczyźnie y=0 wektor pola natężenia elektrycznego w ośrodku pierwszym
znaleźć

w ośrodku drugim. Narysować oba te wektory w chwili t=0.

Dane:

a)
,
;

b)
,
;

Z jakich praw Maxwella wynikają stosowane w zadaniach warunki brzegowe?

Rozw.

1. Rozłożyć wektor pola w ośrodku pierwszym na styczny i normalny do powierzchni rozgraniczenia. Skorzystać z odpowiednich warunków ciągłości. Wynik końcowy to złożenie pól stycznego i normalnego po drugiej stronie powierzchni rozgraniczenia.

Wynik:
;

2. Skorzystać z warunku ciągłości wektorów pola elektrycznego zawierającego ładunek powierzchniowy. Wynik:
   ;

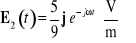
Zad. 2.

Przy przejściu przez granicę dwóch ośrodków (y=0) wartość wektora
wzrosła dwukrotnie. Drugim ośrodkiem jest próżnia. Na granicy ośrodków nie ma ładunków. Znaleźć ε_w pierwszego ośrodka.

Rozw.

Wykorzystujemy warunek brzegowy wiążący składowe pola elektrycznego w obu ośrodkach, normalne do powierzchni rozgraniczenia.

Zad. 3.

Dane są dwa ośrodki:

1.
dla y<0;

2.
dla y>0;

Prąd powierzchniowy płynący po granicy dwóch ośrodków y=0 ma gęstość
. Mając dany wektor
znaleźć
. Narysować oba wektory H oraz wektor
w chwili t=0.

Dane:

a)
,
;

b)
,
.

Z jakich praw Maxwella wynikają wykorzystane tutaj warunki brzegowe?

Rozw.

a) Zastosować warunki brzegowe dla składowych normalnych oraz stycznych do powierzchni.

Wynik:

b) tutaj stosujemy te z warunków brzegowych, w których występują prądy powierzchniowe:

Wynik:

FALA PADAJĄCA PROSTOPADLE NA GRANICĘ DWÓCH OŚRODKÓW

Najpierw kilka przykładów.

Przykład 1. Zakładamy, że na płaszczyznę z=0, stanowiącą granicę dwóch ośrodków pada fala płaska TEM. Pierwszym ośrodkiem jest próżnia, drugim (dla
) jest przewodnik, scharakteryzowany stałymi
, natomiast częstotliwość spełnia warunek
. Fala padając prostopadle wnika w metal. Nie wchodząc w zagadnienie odbić od granicy ośrodków przy takim padaniu fali, zakładamy, że w płaszczyźnie z = 0 istnieje pole magnetyczne:

(amplituda przyjęta tutaj w opisie jest podwojoną jakąś wartością H₀, dla spójności z ogólną teorią odbić na granicy dwóch ośrodków i innymi przykładami). W zapisie powyższym podkreślono wyraźnie ciągłość pola magnetycznego na granicy dwóch ośrodków.

Fala elektromagnetyczna wnika prostopadle w przewodnik, gdzie jak wiadomo, ulega silnemu tłumieniu. Korzystając z zależności podanych na wykładzie, dotyczących fal w przewodnikach rzeczywistych, możemy tę fale opisać następująco:

pole magnet.
oraz pole elektr.

przy czym
oraz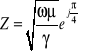
.

Pole elektryczne fali powoduje przepływ prądu o dużej gęstości objętościowej:

.

Gęstość objętościowa prądu jest duża w pobliżu granicy dwóch ośrodków, ale szybko zanika przy oddalaniu się w głąb przewodnika. Rozkład prądu w przestrzeni zależy od parametru
. Im większa jest wartość tego parametru, tym większa jest amplituda prądu J w pobliżu płaszczyzny z = 0, ale jednocześnie następuje szybsze zanikanie prądu w kierunku prostopadłym do tej płaszczyzny. Obliczając całkę z gęstości prądu
wzdłuż osi 0z, dostajemy:

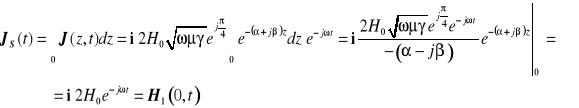
Obliczona całka zależy jedynie od pola magnetycznego na granicy ośrodków. Zastosowaliśmy wobec niej oznaczenie
, gdyż reprezentuje ona całkowity prąd przypadający na jednostkę długości (tutaj liczoną wzdłuż osi 0z).Zwiększenie konduktywności lub częstotliwości powoduje większe skoncentrowanie prądu w pobliżu granicy przewodnika, ale nie zmienia wartości
. Jeśli na przykład fala o częstotliwości 1 GHz wnika w miedź, to niemal cały prąd jest skoncentrowany w warstwie o grubości kilku mikrometrów (w przypadku cienkiej warstwy aluminium powoduje to „strzelanie” w wyniku mikroeksplozji warstwy metalicznej opakowania masła lub margaryny, które chcemy ogrzać w kuchence mikrofalowej). Dla takich właśnie przypadków dogodnie jest przyjąć model, w którym zakłada się nieskończenie cienką warstwę, w której występują prądy. Konsekwencją takiego założenia jest nieskończenie szybkie zanikanie pola magnetycznego w drugim ośrodku, a więc
. W takim więc modelu warunek ciągłości pola magnetycznego na granicy ośrodków zostaje zastąpiony warunkiem:

przy czym

.

Przykład ten wskazuje, że pojęcie prądu powierzchniowego znajduje doskonałe zastosowanie w przypadku, gdy jeden z ośrodków jest dobrym przewodnikiem, a częstotliwość pola jest duża. Wtedy właśnie, m.in. przy rozwiązywaniu niektórych zadań, stosuje się opis uproszczony, gdzie pole magnetyczne zmienia się skokowo, a prąd płynie warstwa nieskończenie cienką.

Przykład 2. Rozważamy warunki brzegowe dla pól zmiennych w czasie, na granicy dielektryka i idealnego przewodnika (ośrodek drugi).

W ośrodku drugim pole elektryczne musi być równe zeru, gdyż w przeciwnym wypadku wywoływałoby przepływ prądu o nieskończonym natężeniu. Istnienie w tym ośrodku zmiennego pola magnetycznego jest również niemożliwe, ponieważ zgodnie z prawami indukcji musiałoby ono wywołać pole elektryczne, co byłoby sprzeczne z poprzednim stwierdzeniem. W rezultacie cztery znane dotąd warunki brzegowe przyjmują postać:

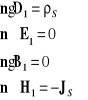
Z powyższych wzorów wynika, że pole elektryczne na granicy przewodnika idealnego jest prostopadłe, a pole magnetyczne równoległe do tej granicy.

Przykład 3. Rozważamy falę padającą prostopadle z próżni na powierzchnię przewodnika (płaszczyzna z=0) o danych
przy czym
.

Impedancja drugiego ośrodka wyraża się wzorem (patrz wykład )

Ponieważ
(sprawdzić samodzielnie), więc współczynnik odbicia
.

(sprawdzić, dlaczego nie jeden i co to mówi o fazie sygnału odbitego)

Pola elektryczne i magnetyczne (rzeczywiste) w ośrodku pierwszym wyrażają się zależnościami

Fala padająca:

oraz fala odbita:

~

Dla wyznaczenia pola w ośrodku 1 skorzystać warto z nst. zależności trygonometrycznych:

oraz

Z uwzględnieniem powyższych zapisów pole w ośrodku pierwszym wyrazi się zależnościami:

oraz

współczynnik propagacji fali w ośrodku drugim (patrz wykład) wyniesie

, a dla przewodnika mamy
.

Korzystając z warunku ciągłości składowej stycznej pola magnetycznego na granicy ośrodków, wektor pola magnetycznego w ośrodku drugim możemy zapisać w postaci:

natomiast wyrażenie opisujące wektor pola elektrycznego łatwo uzyskamy korzystając ze znajomości impedancji ośrodka drugiego, a wtedy

W pierwszym ośrodku mamy do czynienia (zakładając przybliżona wartość współczynnika odbicia równą -1) z falą stojącą, której minimum pola elektrycznego i maksimum pola magnetycznego występują an granicy próżnia-przewodnik. W ośrodku drugim (w przewodniku) mamy do czynienia z falą biegnącą w kierunku osi +0z, bardzo silnie tłumiona, malejącą e-krotnie na odcinku o długości z=
(co wynika z definicji i roli współczynnika tłumienia
). Bazując na przykładzie 1-szym, można zastosować dla materiałów o bardzo dobrej przewodności, dla wysokich częstotliwości fali padającej, model uproszczony, gdzie przyjmuje się
oraz
, a wtedy na powierzchni granicznej płynie prąd powierzchniowy:

.

Zad. 4.

Na doskonale przewodzącą grubą płytę pada z próżni prostopadle do powierzchni płyty (x=0) fala elektromagnetyczna, której wektor
dany jest w postaci:
.

Znaleźć równanie opisujące wektor gęstości prądu
płynącego po powierzchni płyty.

Rozw.

Stosujemy model przybliżony zakładający brak pola elektrycznego i magnetycznego wewnątrz przewodnika doskonałego. Obliczamy wektor

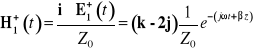
stąd

Zad. 5.

Po powierzchni (płaszczyzna z=0) przewodzącej nieskończenie cienkiej płyty płynie prąd o gęstości
. Określić w półprzestrzeni
wektory E oraz H fali wywołanej przez ten prąd.

Rozw.

Po obu stronach płyty wektory E muszą być identyczne, natomiast wielkość wektorów H jest taka sama, ale ich kierunek przeciwny. Energia prądu rozdziela się po połowie na energie promieniowane w prawo i w lewo od płyty. Stąd mamy

a stąd

Ostatecznie mamy

oraz

.

Zad. 6.

Fala elektromagnetyczna pada prostopadle na płytę przewodzącą o konduktywności
. Jaki kąt tworzą ze sobą wektor pola elektrycznego fali padającej oraz wektor prądu płynącego w metalu?

Przechodząc w granicy do
należy określić, jaki kąt tworzą ze sobą wektory
oraz
w przypadku padania prostopadłego na płytę doskonale przewodzącą.

Rozw.

Z ciągłości składowych stycznych wektora E (zajrzeć do warunków brzegowych i sprawdzić) wynika, że wektory E przed płytą i w płycie przewodzącej są współliniowe, więc tworzą kąt
. Ponieważ gęstość prądu
, więc wektory E i J są współliniowe. Wynika stąd, że w przypadku doskonałego przewodnika wektory J_s i E są równoległe.

FALOWÓD PROSTOKĄTNY

Zad 7.

W falowodzie prostokątnym o bokach a=10 cm, b=5 cm wzbudzamy falę elektromagnetyczną przestrajając generator od f=0 do f=3 GHz. Wypisać rodzaje fal w kolejności ich wzbudzania.

Rozw.

TE_1,0, TE _0,1,TE_2,0

Zad.8

W falowodzie o bokach a=5cm, b=3cm, wypełnionym powietrzem rozchodzi się fala o częstotliwości f=3,3 GHz.

Znając maksymalną amplitudę pola elektrycznego
należy obliczyć:

1. amplitudę składowej prostopadłej wektora H;

2. maksymalną wartość składowej wzdłużnej prądu płynącego w ściankach;

Rozw.

a) Ponieważ rozchodzi się tutaj tylko fala typu TE_1,0 (co najpierw trzeba wywnioskować z odpowiednich znanych już obliczeń), mamy zależność na impedancję falowodu:

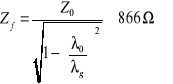
Wtedy

b)

Zad. 9.

Falowód o bokach a = 7,07 cm, b = 3 cm jest pobudzany drganiami o częstotliwości f =3GHz. Należy okreścić:

1. które rodzaje fal mogą się rozchodzić;

2. obliczyć
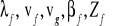
   dla rodzaju podstawowego.

Rozw.

a)
, fale o innych rodzajach nie mogą się rozchodzić.(relacje dla długości fali można też zrealizować dla częstości
).

b)
,
,
,
,
.

---