TRANSPORT MASY

Transport masy występuje pod wpływem gradientów koncentracji, które są wtym przypadku tzw. siła napędową transportu. Przepływ płynów pod wpływem gradientów ciśnień nazywa się często transportem objętościowym i nie jest związany z dyfuzyjnym transportem masy.

Dyfuzyjny transport masy w nieruchomej lub laminarnej warstwie płynu występuje pod wpływem chaotycznych ruchów molekuł. Transport masy w tym przypadku polega na wyrównywaniu się stężenia w obszarze występowania gradientów stężeń czyli w tzw. polu stężeń. Podczas przepływu burzliwego płynu transport dyfuzyjny jest wspomagany przez konwekcję. Konwekcja polega na przenoszeniu całych porcji płynu w wyniku działania wirów lub strumieni.. Konwekcja prowadzi również do wyrównywania się stężeń w badanym obszarze.

Szybkość (kinetyka) transportu masy ma decydujące znaczenie dla przebiegu wielu procesów np. w bioreaktorach. Czas przebiegu biokonwersji mikrobiologicznej czy enzymatycznej zależy nie tylko od szybkości reakcji biochemicznej ale jest limitowana szybkością doprowadzania produktów i odprowadzania substratów z otoczenia mikroorganizmu. Zwykle w otoczeniu mikroorganizmu tj. na przestrzeni między jego powierzchnią i rdzeniem powstaje tzw. stężeniowa warstewka przyścienna, w której zmiana stężenia substratów lub produktów ma decydujące znaczenie dla szybkości transportu masy.

Warstewka przyścienna izoluje mikroorganizm od środowiska bioreaktora i od dostępu do substratów np. tlenu oraz ogranicza wydalanie metabolitów, które są często inhibitorami reakcji biochemicznej. Stężenia produktów i substratów w tej warstewce, a nie w rdzeniu (bioreaktorze) decydują o przebiegu i szybkości reakcji. Intensywne mieszanie pozwala zredukować grubość tej warstewki ale jej nigdy nie wyeliminuje.

Warstewką przyścienną nazywamy obszar w otoczeniu powierzchni międzyfazowej, w którym występuje gradient odpowiedniego potencjału a więc stężenia, temperatury lub prędkości. Możliwe jest więc występowanie niezależnie warstewki stężeniowej, temperaturowej czy hydrodynamicznej. Równania fenomenologiczne opisują strumienie ciepła, masy lub pędu w zależności od odpowiednich gradientów potencjałów w warstewkach oraz od tzw. współczynników kinetycznych charakteryzujących środowisko (ośrodek) w którym odbywa się transport tych strumieni. Transport masy, ciepła lub pędu w warstewckach przyściennych odbywa się z określoną prędkośćią którą można kontrolować poprzez aranżowanie odpowiednich warunków hydrodynamicznych w aparaturze procesowej Rdzeniem nazywamy obszar w którym występuje pełne przemieszanie skutkiem, którego temperatura, koncentracja czy prędkość są stałe. Transport masy, pędu lub ciepła w rdzeniu przebiega zawsze z nieskończenie dużą prędkością

 

PROCESY JEDNOSTKOWE ZWIĄZANE Z TRANSPORTEM MASY

Inżynieriaprocesowa jest nauką o procesach jednostkowych tj. takich które stanowią podstawowe elementy każdej technologii chemicznej, przetwórczej i pokrewnych. Procesy jednostkowe związane z transportem masy polegają na przenoszeniu jednego lub wielu składników między co najmniej dwoma fazami poprzez warstewki przyścienne.

Na poniższych rysunkach strzałkami oznaczono kierunek transportu masy składnika między fazami w różnych procesach jednostkowych:

,

destylacja, suszenie, desorpcja

absoprpcja, skraplanie

rektyfikacja

ekstrakcja

ługowanie (ekstrakcja z ciała stałego)

adsorpcja

permeacja gazów

odwrócona osmoza, ultrafiltracja , nanofiltracja, mikrofiltracja, ekstrakcja mebranowa, perstrakcja

destylacja membranowa

perwaporacja

membrany ciekłe i "podparte"

hemodializa, elektrodializa

transport aktywny i ułatwiony

absorpcja membranowa

kontrolowane uwalnianie

RÓWNANIA BILANSU MASY PODCZAS TRANSPORTU DYFUZYJNEGO

Natężenie przepływu masy wybranego składnika i przez powierzchnię jednostkową (A) nazywamy strumieniem masy. Strumień masy może być wyrażony w kilogramach lub w molach na jednostkę czasu i powierzchni.

: lub

Strumień masy składnika i podczas dyfuzji w polu stężeń w kierunku x jest wyrażony fenomenologicznym równaniem Fick'a:

W ogólnym przypadku podczas transportu nieustalonego możliwa jest akumulacja składnika "i" w każdym miejscu na drodze dyfuzji:

masa dopływająca

masa zakumulowana w elemencie objętości

masa odpływająca

Bilans masy podczas niestacjonarnego transportu masy można przedstawić równaniem:

Biorąc pod uwagę pierwsze prawo Ficka przy wyrażeniu różniczki strumienia otrzymamy ostatecznie równanie nieustalonego i jednokierunkowego transportu masy nazywane drugim prawem Fick'a:

W warunkach stacjonarnych mamy niezmienną w czasie wartość koncentracji związaną z określonym miejscem, a zatem różniczka koncentracji po czasie jest równa zeru:

skąd wynika stałość wyrażenia określającego strumień masy Ni według I prawa Fick'a:

RODZAJE DYFUZYJNEGO TRANSPORTU MASY

1. DYFUZJA RÓWNOMOLOWA PRZECIWKIERUNKOWA

Taki mechanizm transportu dyfuzyjnego występuje w procesie rektyfikacji na powierzchni miedzyfazowej parowo-cieczowej. W tym wypadku molowe ciepło parowania składników o różnych lotnościach są jednakowe co powoduje uwalnianie takiej samej ilości ciepła przy skraplaniu każdego mola składnika mniej lotnego jak potrzebna jest do odparowania jednego mola składnika bardziej lotnego (reguła Troutona):

Podczas dyfuzji gazów w warunkach stałego ciśnienia dyfuzji składnika w jednym kirunku towarzyszy zawsze dyfuzja drugiego składnika w kierunku przeciwym na podstawie prawa Dalton'a:

co implikuje

Z równania stanu gazów wynika proporcjonalność ciśnienia i koncentracji:

zatem

zatem

Z czego wynika równość zmian koncentracji

Teraz stosując prawo Ficka możemy udowodnić równomolowość strumieni:

Po scałkowaniu tej zależności między przekrojami 1-2 otrzymamy formułę obliczeniową dla strumienia masy podczas dyfuzji równomolowej przeciwkierunkowej.

 

2.DYFUZJA JEDNEGO SKŁADNIKA A PRZEZ SKŁADNIK INERTNY B

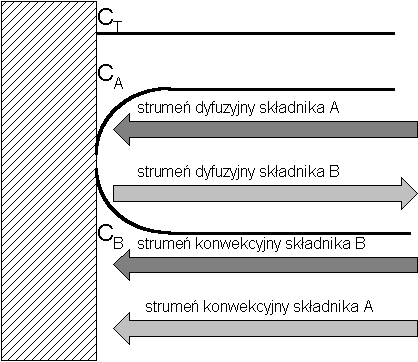
W pewnych przypadkach tylko jeden składnik dyfunduje na skutek selektywnego usuwania właśnie tylko tego składnika w rozmaitych procesach separacji. Na przykład absorpcja tego składnika przez powierzchnię absorbującą w wyniku absorpcji lub chemisorpcji (absorpcja z reakcją chemiczna). Taki mechanizm transportu ma miejsce w otoczeniu mikroorganizmów podczas oddychania lub pobierania z otoczenia określonych produktów, lub ich wydalania.

Powierzchnia pochłaniająca składnik A w wyniku absorpcji lub reakcji chemicznej. Np. Powierzchnia międzyfazowa w procesach jednostkowych lub błona komórkowa

Zmniejszanie się koncentracji składnika A w otoczeniu powierzchni spowoduje powstanie gradientu koncentracji i jest przyczyna dyfuzji składnika A w kierunku powierzchni:

Zmniejszenie się koncentracji składnika A przy powierzchni spowoduje również powstanie pewnej nadwyżki składnika B (gradient koncentracji B) a to z kolei wywoła strumień dyfuzyjny składnika B w przeciwnym kierunku do dyfuzji składnika A.

Przestrzeń w otoczeniu powierzchni absorbującej będzie stale wypełniana przez składniki A i B dopływające tam z rdzenia w wyniku konwekcji. W warunkach ustalonych strumeń konwekcyjny składnika B musi być przy tym równy strumieniowi dyfuzyjnemu tego składnika

Strumień konwekcyjny składnika A będzie pozostawał w stałym stosunku (stężeń) do strumienia konwekcyjnego składnika B, a z tąd:

Po zsumowaniu wszystkich czterech strumieni otrzymamy strumień masy (netto) w pobliżu powierzchni absorbującej jeden składnik A.:

Po zredukowaniu się strumieni konwekcyjnego i dyfuzyjnego składnka B otrzymamy:

Uwzględniając po raz drugi, że strumień konwekcyjny strumienia B jest równy strumieniowi dyfuzyjnemu tego skladnika otrzymamy:

W przypadku występowania tylko dwóch składników gradienty stężeń są zawsze równe i przeciwnie skierowane:

a współczynniki składnika A przez składnik B i odwrotnie dyfuzji są równe:

Po uwzględnieniu powyższych zależności obliczymy ostatecznie strumień netto w kierunku powierzchni:

Po uwzględnieniu dwuskładnikowej kompozycji rozpatrywanej mieszaniny otrzymamy:

Po scałkowaniu tej zależności między dwoma dowolnymi przekrojami 1 i 2 otrzymamy formułę obliczeniową dla strumienia masy podczas dyfuzji jednego składnika A przez inert B na drodze 1-2:

Uwzględniając definicję średniej logarytmicznej stężenia (koncentracji) :

otrzymuje się ostatecznie formułę roboczą do obliczania strumienia składnika A przez inert B:

Dla przypadku dyfuzji składników gazowych powyższe równanie można również zapisać w yrażając stężenia w formie ciśnień cząstkowych:

W przypadku małych stężeń strumień dla przypadku dyfuzji przez inert jest równy strumieniowi obliczonemu jz formuły dla przypadku dyfuzji równomolowej przeciwkierunkowej

3. DYFUZJA JEDNEGO SKŁADNIKA PRZEZ MIESZANINĘ INERTÓW

Ten przypadek występuje bardzo często w realnych układach, jednak jego opis jest trudny i musi uwzględnić wzajemne binarne oddziaływania między składnikami. Jedną z metod opisu dyfuzji wieloskładnikowej jest metoda wzorowana na teorii dyfuzji gazów Maxwell'a. Zakłada się tam, że całkowity gradient ciśnienia składnika A dyfundującego przez mieszaninę inertów jest równa sumie gradientów, które wystąpiłyby w układach binarnych (tj. gdyby składnik A dyfundował kolejno przez czyste składniki B, C, D,...itd).

Zakłada się przy tym, że gradient koncentracji układzie binarnym jest:

1. jest proporcjonalny do różnicy prędkości obu tych składników,

2. jest proporcjonalny do iloczynu koncentracji tych składników.

gdzie FAi jest stałą charakteryzującą układ składników:

Wyrażając stężenia przez koncentracje molowe ( z równania stanu gazów):

otrzymamy wzór na gradient stężenia podczas dyfuzji składnika A przez mieszanine inertów w nowej postaci:

Dla każdego inertu z definicji jego prędkość jest równa zeru, zatem gradient stężenia w ukladzie binarnym możemy zapisać:

Następnie pedkość składnika A można wyrazić za pomocą strumienia molowego i koncentracji molowej (jest to tzw. prędkość dyfuzji):

Zatem gradient stężenia w układzie binarnym określa relacja o postaci:

Całkowity gradient stężenia składnika A podczas jego dyfuzji przez mieszaninę inertów określa więc wzór:

Po przekształceniu tego równania otrzymuje się równanie analogiczne do równania Fick'a ale tym razem dla dyfuzji składnika A przez mieszaninę inertów

Porównanie z pierwszym prawem Fick'a pozwala na określenie zastępczej wartości współczynnika dyfuzji dla przypadku dyfuzji jednego składnika A przez mieszaninę składników o ile znane są wartośći współczynników dyfuzji w układach binarnych:

Po obliczeniu zastępczego współczynnika dyfuzji strumień masy opisuje prawo Fick'a.

WYKORZYSTANIE TEORII MAXWELLA DO OPISU SZCZEGÓLNYCH PRZYPADKÓW DYFUZJI

Teorię maxwella można stosować do opisu wszystkich przypadków dyfuzji po uwzględnieniu odpowiednich założeń. Teoria Maxwella jest zatem uogólnieniem wszystkich przypadków.

1. DYFUZJA RÓWNOMOLOWA PRZECIWKIERUNKOWA

Założenia tego przypadku określają równość strumieni molowych składników A i B przenoszonych w przeciwnych kierunkach:

Prędkości dyfuzju dwóch składników wynoszą więc odpowiednio:

Stałą Maxwella dla tego przypadku przedstawia wzór:

W tym przypadku gradient stężenia można wyrazić wzorem:

Po uproszczeniu i przekształceniu otrzymuje się wcześniej znany (I prawo Fick'a) wzór:

2. STRUMIEŃ PODCZAS DYFUZJI SKŁADNIKA A PRZEZ INERT B

Założenia tego przypadku określają równość strumieni molowych składników A i B przenoszonych w przeciwnych kierunkach:

Prędkości dyfuzji składników wynoszą więc odpowiednio:

W tym przypadku gradient stężenia można wyrazić wzorem

gdzie stałą Maxwella F dla tego przypadku obliczono jak poprzednio

Po uproszczeniu i przekształceniu otrzymuje się wcześniej znany ( prawo Stefana) wzór:

WYZNACZANIE WSPÓŁCZYNNIKÓW DYFUZJI METODĄ WINKELMAN'A

Współczynniki dyfuzji w gazach można wyznaczyć metodą WInkelman'a. Zasadą tej metody jest obserwacja szybkości zmniejszania sie poziomu lustra cieczy w kapilarze. Ciecz paruje a następnie dyfunduje pokonując drogę między lustrem cieczy a wylotem z kapilary. Warunki na wylocie z kapilary są tak dobrane aby stężenie w tym miejscu było równe zeru. W tym celu stosuje się gaz inertny, którego natężenie przepływu jest odpowiednio duże aby koncentracja na wylocie z kapilary była bliska zeru. Stężenie cieczy nad lustrem jest równe stężeniu nasycenia:

Strumień dyfundującej pary na odcinku "L" między powierzchnią międzyfazową a końcem kapilary można obliczyć z prawa Stefana:

Biorąc pod uwagę,że stężenia w przekroju 1 (na wylocie z kapilary jest równe zeru) na skutek "zdmuchiwania" par przez gaz inertny oraz, że stężenie na powierzchni międzyfzowej ma wartość stężenia nasycenia otrzymamy:

Średnią koncentrację inertów B obliczymy uwzględniając formułę średniej logarytmicznej:

Koncentracja nasycenia na powierzchni lustra po stronie fazy gazowej jest proporcjonalna do prężności pary nasyconej () według równania stanu gazów:

z którego wynika również związak między koncentracją całkowitą i ciśnieniem całkowitym fazy gazowej:

Po uwzględnieniu tych zależności koncentrację nasycenia można obliczyć na podstawie prężności pary nasyconej w danej temperaturze, (którą można znależć najczęściej w tablicach):

Koncentrację całkowitą oblicza się korzystając ze stałej objętości właściwej gazów idealnych (22.4 m3/kmol) z uwzględnieniem aktualnej wartości temperatury:

Koncentrację inertów oblicza się jako różnicę:

Na podstawie obserwacji zmiany wysokości słupa cieczy w kapilarze można obliczyć równięż wartość strumienia masy:

Porównując strumienie masowe składnika A wyznaczone na pdstawie prawa Stefana oraz z bezpośredniej obserwacji zmian położenia lustra cie czy otrzymamy zależność:

Po uporządkowaniu otrzymuje się równanie różniczkowe, które po scałkowaniu:

daje relację o postaci:

Dalsze postępowanie polega na wyznaczeniu w drodze eksperymentalnej zależności między szybkośćią dyfuzji a drogą dyfuzji:

Współczynnik dyfuzji wyznacza się na podstawie wartości współczynnika kątowego prostej wyznaczonej w metodą najmniejszych kwadratów.

EMPIRYCZNE FORMUŁY DO OBLICZANIA WSPÓŁCZYNNIKÓW DYFUZJI

Wyniki badań dyfuzji pozwoliły na opracowanie empirycznych formuł. Jedną z nich jest rwnanie Maxwell'a zmodyfikowane przez Gilland'a w którym współczynniki dyfuzji w gazach są zależne od takich własności fizycznych i chemicznych jak masy cząsteczkowe [kg/kmol] i objętości molowe [cm3/mol], temperatura [ K] i ciśnienie [bar]:

Analogiczne równanie empiryczne do obliczania współczynnika dyfuzji w cieczach ma postać:

gdzie współczynnik lepkości  wyrażono w [Pas], objętości molowe [m3/kmol], temperatura[ K].

Objętości molowe cieczy

ciecz	objętość molowa	jednostki
woda	0.008	m3/kmol
metanol	0.015	m3/kmol
benzen	0.228	m3/kmol

Równanie to nie ma zastosowania do elektrolitów i roztworów o wysokich koncentracjach. Stwierdzono, że iloczyn lepkości i dyfuzyjności jest liniwą funkcją koncentracji.

Dyfuzyjność składników w wodzie

układ (składnik A - składnik B)	współczynnik dyfuzji DAB	jednostki
tlen - woda	1.80 10-9		m2/s
dwutlenek węgla - woda	1.50 10-9		m2/s
amoniak-woda	1.76 10-9		m2/s
siarkowodór-woda	1.41 10-9		m2/s
metanol - woda	1.28 10-9		m2/s
propanol - woda	0.87 10-9		m2/s
butanol - woda	0.77 10-9		m2/s
laktoza - woda	0.43 10-9		m2/s
glukoza - woda	0.60 10-9		m2/s
maltoza - woda	0.43 10-9		m2/s
sacharoza - woda	0.45 10-9		m2/s
rafinoza - woda	0.37 10-9		m2/s

Dyfuzyjność składników w powietrzu

układ (składnik A - składnik B)	współczynnik dyfuzji DAB	jednostki
wodór - powietrze	41 10--6	m2/s
woda - powietrze	25 10--6	m2/s
amoniak - powietrze	23 10--6	m2/s
tlen - powietrze	23 10--6	m2/s
dwutlenek węgla - powietrze	20 10--6	m2/s
metanol - powietrze	16 10--6	m2/s
etanol - powietrze	12 10--6	m2/s
propanol - powietrze	10 10--6	m2/s
butanol - powietrze	9 10--6	m2/s
pentanol - powietrze	7 10--6	m2/s
heksanol - powietrze	6 10--6	m2/s

---