PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA w Chełmie Instytut Nauk Technicznych i Lotnictwa Kierunek: Elektrotechnika III rok VI semestr |
|||
LABORATORIUM Z URZĄDZEŃ ELEKTRYCZNYCH |
|||
Temat: Badanie układu do kompensacji mocy biernej |
|||
Data wykonania ćwiczenia 11.05.2014 |
Zespół II |
Ćwiczenie nr 1 |
Podpis |
Cel ćwiczenia
Celem ćwiczenia jest zapoznanie się z idea stosowania kompensacji mocy biernej, poznanie jej pozytywnych jak i negatywnych skutków a także przybliżenie sposobów kompensacji i urządzeń temu służących.
Wykonanie ćwiczenia

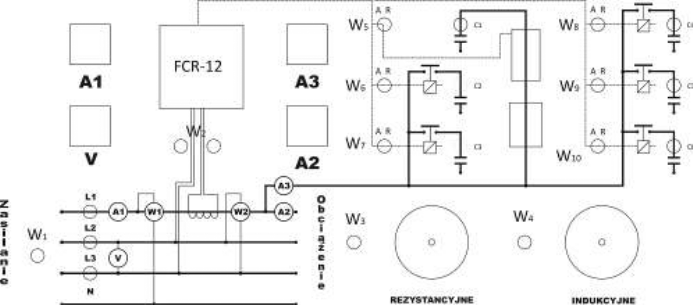
Rys.1. Schemat układu
Oznaczenie przycisków:
W1 - wyłącznik zasilania
W2 - wyłącznik zasilania regulatora FCR-12
W3 - wyłącznik obciążenia rezystancyjnego
W4 - wyłącznik obciążenia indukcyjnego
W5 -:- W10 - wybór rodzaju pracy kondensatorów A- praca automatyczna (za pomocą regulatora mocy), R- praca ręczna.
Pomiar:
V - pomiar napięcia międzyfazowego L2-L3
A1 - pomiar natężenia prądu sieci w fazie pierwszej
A2 - pomiar natężenia prądu w gałęzi z indukcyjnością
A3 - pomiar natężenia prądu w gałęzi z pojemnością
W1 - pomiar mocy czynnej
W2- pomiar mocy biernej indukcyjnej
W układzie rozróżniamy dwa tryby pracy:
Wyłączniki W5 ÷W10 w pozycji „A” - praca w trybie automatycznym (praca regulatora FCR)
Wyłączniki W5 ÷W10 w pozycji „R” - praca w trybie ręcznym
Stopnie kondensatorowe zastosowane w układzie:
C1 = 16 μF 420 V
C2 = 10 μF 500 V
C3 = 13 μF 500 V
C4 = 7,5 μF 450 V
C5 = 6 μF 475 V
C6 = 3 μF 475 V
Oznaczenia z tabel:
Us - napięcie międzyfazowe sieci zasilającej (wskazanie woltomierza V)
I1- prąd pobierany z sieci (wskazania amperomierza A1)
I2 - prąd obciążenia (wskazania amperomierza A2)
I3 - prąd baterii kondensatorów (wskazania amperomierza A3)
P' - wskazania watomierza W1
Q'1L, Q'1 - wskazania watomierza W2 bez kompensacji (otwarte wyłączniki W5-W10)
Q'2C, Q'2 - wskazania watomierza W2 z kompensacja (zamknięte wyłączniki W5-W10)
I0 - prąd pobierany przez odbiorniki
S - moc pozorna układu
P - moc czynna pobierana przez układ
Q1 - moc bierna układu bez kompensacji
Q2 - moc bierna układu przy częściowej kompensacji
QC - moc bierna baterii kondensatorów
cosφ - współczynnik mocy układu
tgφ - stosunek mocy biernej i czynnej
Wyznaczenie charakterystycznych wielkości układu odbiorczego bez kompensacji i z częściową kompensacją mocy dla stałej wartości obciążenia mocą bierną indukcyjną
Tabela 1. Wyznaczanie charakterystycznych wielkości układu odbiorczego bez kompensacji i z częściową kompensacja mocy biernej dla stałej wartości obciążenia indukcyjnego
Lp. |
Pomiar |
Obliczenia |
|||||||||||||
|
US |
I1 |
I2 |
I3 |
P' |
Q'1L |
Q'2C |
cosφ |
I0 |
S |
P |
Q1 |
Q2 |
QC |
cosφ |
|
V |
A |
A |
A |
W |
var |
var |
- |
A |
VA |
W |
var |
var |
var |
- |
1. |
404,0 |
3,47 |
3,43 |
0,00 |
200 |
1460 |
|
0,22 |
|
2428,13 |
600 |
2528,79 |
|
0,00 |
0,23 |
2. |
403,3 |
2,74 |
3,42 |
1,16 |
200 |
1000 |
|
0,31 |
|
1913,99 |
600 |
1732,05 |
|
810,30 |
0,33 |
3. |
402,9 |
2,43 |
3,44 |
1,91 |
200 |
700 |
|
0,43 |
|
1695,76 |
600 |
1212,44 |
|
1332,88 |
0,44 |
4. |
402,5 |
2,22 |
3,44 |
2,83 |
210 |
340 |
|
0,72 |
|
1547,67 |
630 |
588,90 |
|
1972,94 |
0,73 |
5. |
402,4 |
2,19 |
3,43 |
3,38 |
210 |
120 |
|
0,93 |
|
1526,38 |
630 |
207,85 |
|
2355,78 |
0,95 |
6. |
403,0 |
2,25 |
3,43 |
3,45 |
210 |
|
60 |
0,99 |
|
1570,54 |
630 |
|
103,92 |
2408,16 |
0,99 |
7. |
402,7 |
2,29 |
3,46 |
4,04 |
220 |
|
120 |
0,96 |
|
1597,27 |
660 |
|
207,85 |
2817,89 |
0,95 |
Przykładowe obliczenia:
S = ![]()
Us * I1 = ![]()
* 404 * 3,47 ≈ 2428,13 VA
P = 3P' = 3 * 200 = 600 W
Q1 = ![]()
Q'1L = ![]()
* 1460 ≈ 2528,79 var
Q2 = ![]()
Q'2C = ![]()
* 60 ≈ 103,92 var
QC = ![]()
Us * I3 = ![]()
* 404 * 0 = 0 var
cosφ = P/(P2 + Q2)1/2 = 600/(6002 + 2528,792)1/2 ≈ 0,23
Wykresy fazorowe prądów, napięć i trójkąt mocy
Wartości wyskalowane:
1A- 0,25 A ; 1V- 2cm
Bez kompensacji (wiersz 1 w tabeli 1)
Z częściową kompensacją (wiersz 3 z tabeli 1)
Trójkąt mocy przy częściowej kompensacji (wiersz 3 z tabeli 1)
Wartości mocy wyskalowane w stosunku 1[W, V∙A, var] - 0,3 cm
Wyznaczanie charakterystycznych wielkości układu odbiorczego bez kompensacji i z częściową kompensacją mocy biernej dla zmiennej wartości obciążenia indukcyjnego
Tabela 2. Wyznaczanie charakterystycznych wielkości układu odbiorczego bez kompensacji i z częściową kompensacja mocy biernej dla zmiennej wartości obciążenia indukcyjnego
Lp. |
Pomiar |
Obliczenia |
|||||||||||||
|
US |
I1 |
I2 |
I3 |
P' |
Q'1 |
Q'2 |
cosφ |
I0 |
S |
P |
Q1 |
Q2 |
QC |
cosφ |
|
V |
A |
A |
A |
W |
var |
var |
- |
A |
VA |
W |
var |
var |
var |
- |
1. |
401,8 |
0,77 |
0,75 |
0,00 |
125 |
200 |
|
0,73 |
|
535,87 |
375 |
346,41 |
|
0 |
0,73 |
komp. |
402,5 |
0,62 |
0,75 |
0,47 |
125 |
|
1 |
0,99 |
|
432,23 |
375 |
|
1,73 |
327,66 |
|
2. |
402,2 |
1,17 |
1,16 |
0,00 |
140 |
400 |
|
0,69 |
|
815,06 |
420 |
692,82 |
|
0,00 |
0,52 |
komp. |
402,7 |
0,77 |
1,15 |
0,94 |
112 |
|
5 |
0,99 |
|
537,07 |
336 |
|
8,66 |
655,65 |
|
3. |
403,0 |
1,61 |
1,57 |
0,00 |
150 |
600 |
|
0,37 |
|
1123,81 |
450 |
1039,23 |
|
0,00 |
0,40 |
komp. |
402,1 |
0,93 |
1,57 |
1,53 |
155 |
|
0 |
1,00 |
|
647,71 |
465 |
|
0,00 |
1065,58 |
|
4. |
402,6 |
2,01 |
1,96 |
0,00 |
155 |
800 |
|
0,30 |
|
1401,62 |
465 |
1385,64 |
|
0,00 |
0,32 |
komp. |
403,2 |
1,21 |
1,99 |
1,99 |
165 |
|
4 |
0,99 |
|
845,02 |
495 |
|
6,93 |
1389,74 |
|
5. |
402,4 |
2,45 |
2,43 |
0,00 |
165 |
1000 |
|
0,25 |
|
1707,59 |
495 |
1732,05 |
|
0,00 |
0,27 |
komp. |
402,2 |
1,51 |
2,45 |
2,45 |
175 |
|
2 |
0,98 |
|
1051,91 |
525 |
|
3,46 |
1706,75 |
|
6. |
402,5 |
2,84 |
2,80 |
0,00 |
175 |
1200 |
|
0,23 |
|
1979,91 |
525 |
2078,46 |
|
0,00 |
0,25 |
komp. |
402,7 |
1,80 |
2,83 |
3,04 |
185 |
|
0 |
1,00 |
|
1255,49 |
555 |
|
0,00 |
2120,39 |
|
7. |
402,5 |
3,28 |
3,24 |
0,00 |
190 |
1400 |
|
0,21 |
|
2286,65 |
570 |
2424,87 |
|
0,00 |
0,23 |
komp. |
402,4 |
2,12 |
3,28 |
3,60 |
200 |
|
0 |
1,00 |
|
1477,59 |
600 |
|
0,00 |
2509,12 |
|
8 |
402,3 |
3,68 |
3,63 |
0,00 |
200 |
1600 |
|
0,20 |
|
2564,24 |
600 |
2771,28 |
|
0,00 |
0,21 |
komp. |
402,4 |
2,41 |
3,68 |
4,04 |
205 |
|
1 |
1,00 |
|
1679,72 |
615 |
|
1,73 |
2564,88 |
|
Przykładowe obliczenia:
S = ![]()
Us * I1 = ![]()
* 401,8 * 0,77 ≈ 535,87 VA
P = 3P' = 3 * 125 = 375 W
Q1 = ![]()
Q'1 = ![]()
* 200 ≈ 346,41 var
Q2 = ![]()
Q'2 = ![]()
* 1 ≈ 1,73 var
QC = ![]()
Us * I3 = ![]()
* 401,8 * 0 = 0 var
cosφ = P/(P2 + Q2)1/2 = 375/(3752 + 346,412)1/2 ≈ 0,73
Wykresy
Wykres 1. Charakterystyka współczynnika mocy w funkcji prądu obciążenia cosφ=f(I)
Wykres 2. Wykres zależności wartości prądu pobieranego z sieci I1 od prądu obciążenia I2, z kompensacją i bez kompensacji.
Wnioski
Przeprowadzone ćwiczenie wyraźnie wykazało na czym polega zasada kompensacji mocy biernej i jakie daje korzyści. Pomiary przy stałym obciążeniu indukcyjnym wykazały, że wraz z załączaniem kolejnych pojemności i wzrostem współczynnika mocy cos φ maleje wartość prądu pobieranego z sieci. Pomiar drugi, przy zmiennym obciążeniu, wykazał że zwiększanie obciążenia indukcyjnego powoduje spadek współczynnika mocy czynnej i wzrost wartości prądu pobieranego z sieci. Przy załączaniu kondensatorów poprawiających współczynnik mocy do wartości bliskiej jedności wartość prądu pobieranego z sieci znacznie malała przy takim samym obciążeniu indukcyjnym.
Zjawisko to jest niezmiernie ważne w energetyce, gdyż pozwala ograniczyć wartość prądów przesyłu co powoduje zwiększenie zdolności przesyłowych linii.
1
Ic