Wydział Elektryczny |
Dzień /godzina Poniedziałek 1415-17 Data: 11-03-2002 |
Nr zespołu 3 |
|
Nazwisko i imię
|
Ocena z przygotowania |
Ocena z sprawozdana |
Ocena |
Prowadzący: |
Podpis prowadzącego: |
||
Temat ćwiczenia;
„Pomiar długości fali elektromagnetycznej
metodami interferencyjnymi”
Cel ćwiczenia:
Celem ćwiczenia było wyznaczenie długości fal elektromagnetycznych. Zastosowano metody interferencyjne.
Falami elektromagnetycznymi nazywamy rozchodzące się w przestrzeni zaburzenia pola elektromagnetycznego. Fale te są falami poprzecznym. Fale elektromagnetyczne ulegają zjawisku dyfrakcji i interferencji.
Fala płaska padając na przeszkodę ulega ugięciu.
Interferencja polega na nakładaniu się wiązek falowych. Aby możliwe było otrzymanie obrazu interferencyjnego stabilnego nakładające się fale muszą być spójne (posiadać tą samą częstotliwość i stałą w czasie różnicę faz). Wynikiem tego może być wzmocnienie lub osłabienie natężenia fali wypadkowej.
Wzmocnienie następuje gdy fale nakładają się w fazach zgodnych - różnica dróg optycznych fal jest liczbą naturalną:
∆ = m λ ,
gdzie:
λ - długość fali,
m - liczba naturalna.
Osłabienie następuje w momencie nałożenia się fal o fazach przeciwnych:
∆ = (2m + 1) .
Długość fal elektromagnetycznych można wyznaczyć za pomocą:
interferometrów: Michelsona, Fabry - Perota oraz za pomocą siatki dyfrakcyjnej.
Opis urządzeń pomiarowych;
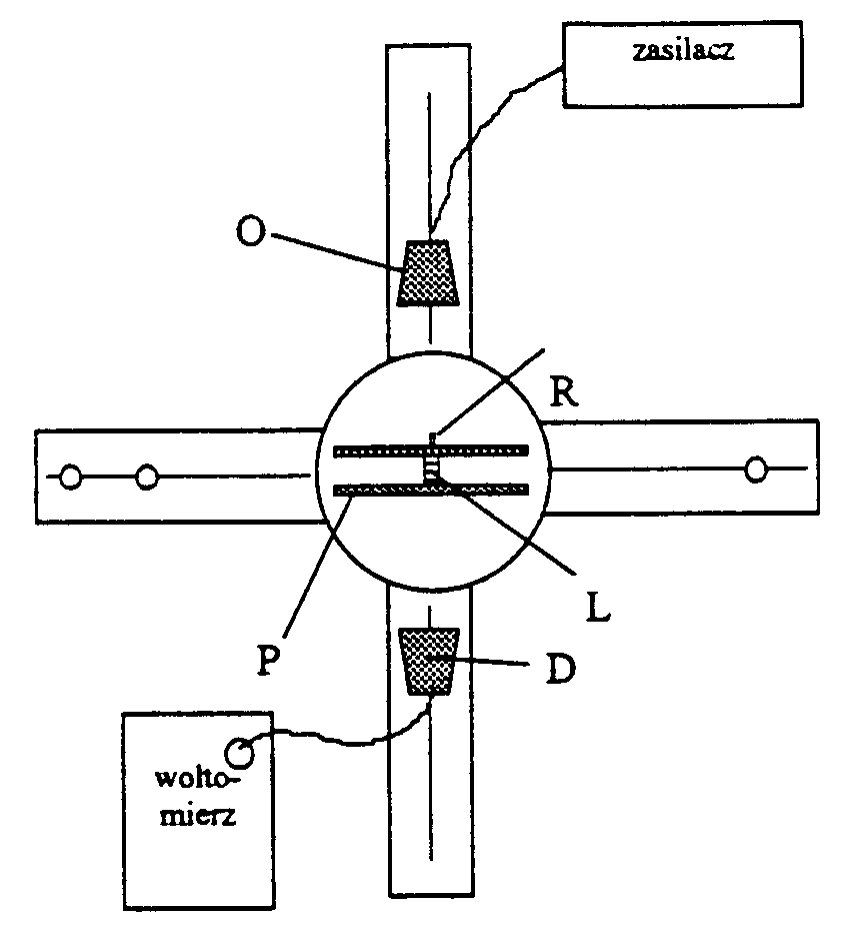
Zasada działania interferometru Fabry - Perota:
Interferometr Fabry-Perota składa się z dwóch płytek, równoległych, oddalonych od siebie o odległość d. Posiadają one zdolność do przepuszczania i odbijania fal elektromagnetycznych. Powietrze między płytkami tworzy płasko równoległą warstwę. Część fal po przejściu przez pierwszą płytkę przechodzi, a część odbija się wielokrotnie od płytki drugiej, zanim przejdzie przez nią.
Ze względu na fakt, iż kąt padania równy jest kątowi odbicia, zarówno fale wchodzące jak i wychodzące z pomiędzy płytek, są do siebie równoległe.
Ze względu na fakt odbijania się fali (2) od płytek wytwarza się różnica dróg optycznych, wynosząca:
Δ = OA + AB- B'R
O - emiter fal,
P - płytki,
R - pokrętło do regulacji odległości między płytkami,
L - linijka,
D - detektor.
Zmieniając odległość (d) między płytkami zmieniamy różnicę dróg optycznych (Δ). Wzmocnienie uzyskiwane jest dla takich dm, dla których:
Δ = 2dm cosα = m λ
Długość fali elektromagnetycznej obliczamy ze wzoru:
λ = cosα(dm+1 - dm)
Zasada działania interferometru Michelsona:
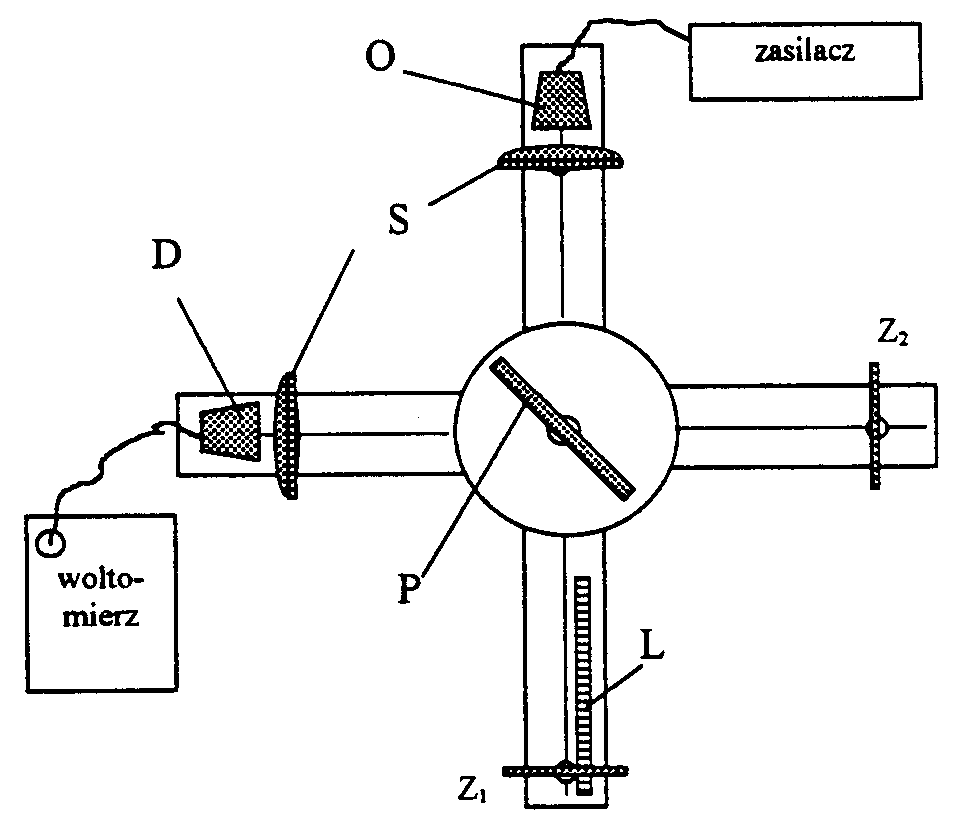
O - emiter fal,
S - soczewki,
D - detektor fal,
Z1, Z2 - zwierciadła,
P - płytka półprzepuszczalna
L - linijka.
Wiązka fal elektromagnetycznych wychodzi ze źródła (O) i pada na płytkę półprzepuszczalną (P). Część fali przechodzi przez płytkę, a część ulega odbiciu. Wiązka odbijająca się od płytki pada na zwierciadło Z2 i wraca odbijając się od niego. Natomiast wiązka przechodząca przez płytkę pada prostopadle na zwierciadło Z1, po odbiciu wraca tą samą drogą. W zależności od ustawienia zwierciadła Z1 (jego odległość od płytki P) fale spotykają się przesunięte w fazie lub nie. Odbiją się od płytki i padają na detektor.
Jeżeli różnica dróg optycznych będzie liczbą naturalną (brak przesunięcia w fazie) następuje wzmocnienie, daje się to zaobserwować wychyleniem wskazówki woltomierza (maksymalne wskazanie woltomierza).
Odsuwając zwierciadło zmieniamy drogę, którą musi pokonać fala elektromagnetyczna. Różnica dróg optycznych jest możliwa do wyznaczenia poprzez kolejne wskazania maksimów na woltomierzu, przy odpowiednich odległościach zwierciadła (Z1) od płytki (P). Ze względu na dwukrotne pokonywanie, przez falę, odległości Z1P długość fali możliwa jest do wyznaczenia według podanego poniżej wzoru:
λ = ,
gdzie:
δ - przesunięcie zwierciadła Z1
m - kolejne zmiany maksymalnych wzmocnień.
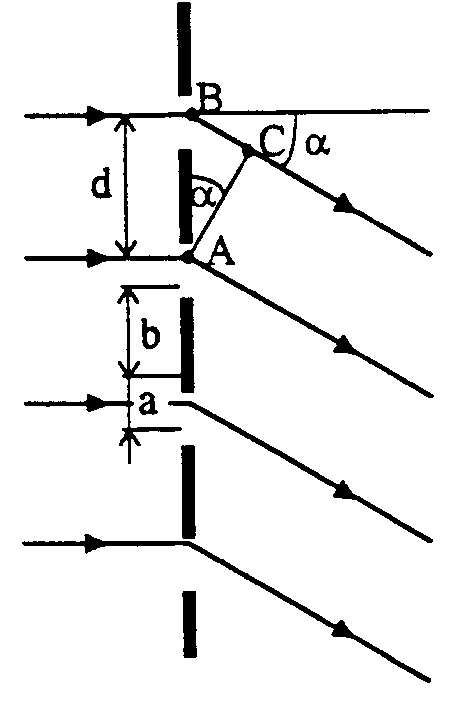
Siatka dyfrakcyjna
Siatką dyfrakcyjną nazywamy układ N równoległych do siebie szczelin rozmieszczonych w równych odstępach. Odległość środków tych szczelin nazywamy stałą siatki dyfrakcyjnej i oznaczamy jako d.
Zgodnie z zasadą Huyghensa, każda szczelina staje się wtórnym źródłem fal, które rozchodzą się we wszystkich kierunkach. Rozpatrzmy fale biegnące od dwóch szczelin, rozchodzące się pod katem . Jak widać z rysunku , różnica ich dróg wynosi =BC i z zależności w trójkącie ABC otrzymujemy =dsin, gdzie nazywamy kątem ugięcia. Wzajemne wzmacnianie się fal uzyskujemy wówczas, gdy
d sinm = m
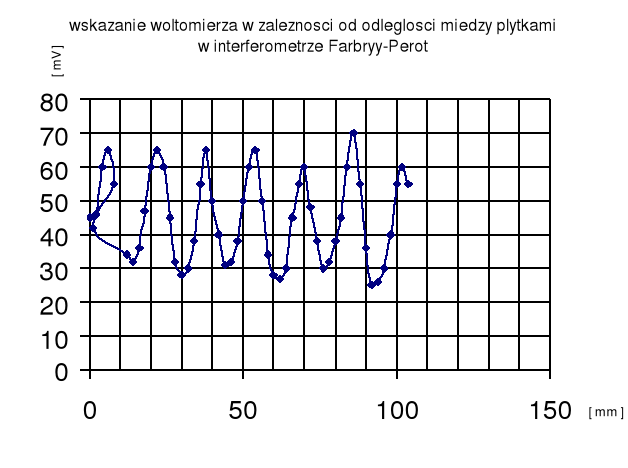
Pomiar długości fali elektromagnetycznej za pomocą Interferometru Fabry-Perota.
Wnioski:
fabry-perot |
|
odleglosc |
mV |
104 |
55 |
102 |
60 |
100 |
55 |
98 |
40 |
96 |
30 |
94 |
26 |
92 |
25 |
90 |
36 |
88 |
55 |
86 |
70 |
84 |
60 |
82 |
45 |
80 |
38 |
78 |
32 |
76 |
30 |
74 |
38 |
72 |
48 |
70 |
60 |
68 |
55 |
66 |
45 |
64 |
30 |
62 |
27 |
60 |
28 |
58 |
34 |
56 |
50 |
54 |
65 |
52 |
60 |
50 |
50 |
48 |
38 |
46 |
32 |
44 |
31 |
42 |
40 |
40 |
50 |
38 |
65 |
36 |
55 |
34 |
38 |
32 |
30 |
30 |
28 |
28 |
32 |
26 |
45 |
24 |
60 |
22 |
65 |
20 |
60 |
18 |
47 |
16 |
36 |
14 |
32 |
12 |
34 |
1 |
42 |
8 |
55 |
6 |
65 |
4 |
60 |
2 |
46 |
0 |
45 |
Liczba pomiarów maksimów n |
Wskazania linijki l |
Wskazanie woltomierza |
Różnica odległości między kolejnymi maksimami la |
- |
mm |
mV |
mm |
1 |
6 |
65 |
- |
2 |
22 |
65 |
16 |
3 |
38 |
65 |
16 |
4 |
54 |
65 |
16 |
5 |
70 |
60 |
16 |
6 |
86 |
70 |
16 |
7 |
102 |
60 |
16 |
∆l=1mm
la=16,00mm
r = 7
α =
dm+r = 102 mm
dm = 6 mm
Długość fali dla Interferometru Fabry-Perota wyraża się wzorem:
![]()
Po podstawieniu otrzymujemy długość fali równą:
λ= 27,39mm
Błąd względny obliczamy metodą pochodnej logarytmicznej:
![]()
gdzie Δn=0
ostatecznie:
![]()
-zmieic wartosci!!!!!!!!!!!!!!!!!!!!!!!!
Ostatecznie długość fali elektromagnetycznej zmierzona za pomocą Interferometru Fabry-Perota wynosi: λ=27,39±1,71mm
) Pomiar długości fali elektromagnetycznej za pomocą siatki dyfrakcyjnej.
siatka dyfrakcyjna |
|
|
kat |
w prawo |
w lewo |
90 |
14 |
14 |
88 |
16 |
17 |
86 |
27 |
25 |
84 |
37 |
38 |
82 |
55 |
50 |
80 |
55 |
55 |
78 |
60 |
55 |
76 |
61 |
30 |
74 |
38 |
12 |
72 |
16 |
15 |
70 |
4 |
3 |
68 |
1,5 |
1 |
66 |
6,5 |
6 |
64 |
17 |
14 |
62 |
26 |
26 |
60 |
27 |
30 |
58 |
20 |
18 |
56 |
10,5 |
12 |
54 |
7 |
11 |
52 |
11 |
13 |
50 |
11 |
9 |
48 |
6,5 |
4,5 |
46 |
2,5 |
2,5 |
44 |
2,5 |
4,5 |
42 |
4,5 |
9,5 |
40 |
11 |
18 |
38 |
16 |
18 |
36 |
14 |
9 |
34 |
5 |
2 |
32 |
2 |
1 |
30 |
1,5 |
1,5 |
28 |
3 |
4 |
26 |
3 |
5 |
24 |
3,5 |
3 |
22 |
15 |
1 |
20 |
8,5 |
1,5 |
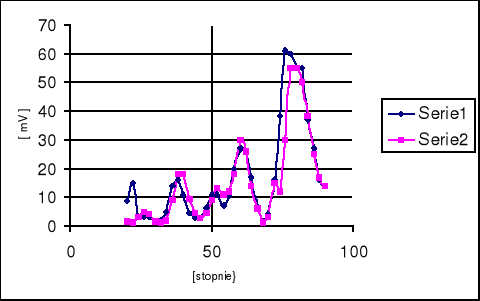
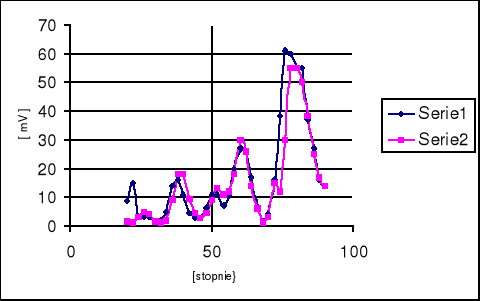
Poniższa tabela przedstawia wyniki pomiarów przeprowadzonych dla siatki dyfrakcyjnej.
Kolejne maksima n |
Miara kąta α |
Wskazania woltomierza |
Długość fali λ |
- |
[ °] |
mV |
mm |
1 w lewo |
26 |
5 |
40,1109 |
2 w lewo |
38 |
18 |
28,1666 |
3 w lewo |
52 |
13 |
24,0343 |
4 w lewo |
60 |
30 |
19,8103 |
5 w lewo |
80 |
55 |
18,0220 |
1 w prawo |
22 |
15 |
34,2765 |
2 w prawo |
38 |
16 |
28,1665 |
3 w prawo |
52 |
11 |
24,0343 |
4 w prawo |
60 |
27 |
19,8103 |
5 w prawo |
76 |
61 |
17,7564 |
Stała siatki d = 91,5mm
Δd=1mm
Δα=1°=0,017rad
Długość fali (dla siatki dyfrakcyjnej) wyraża się wzorem:
![]()
Błąd względny obliczamy za pomocą pochodnej logarytmicznej:
![]()
gdzie: Δn=0.
więc:
![]()
średnia długość fali:
dla n=1 lewo i prawo
![]()
zmienic na 37,19
![]()
- zmien na 1.83
Ostatecznie średnia długość fali elektromagnetycznej zmierzona siatką dyfrakcyjną wynosi:
λśr=(37,19±1,83)mm
średnia długość fali:
dla n=2 lewo i prawo
![]()
zmienic na 28,17
![]()
- zmien na 0,92
Ostatecznie średnia długość fali elektromagnetycznej zmierzona siatką dyfrakcyjną wynosi:
λśr=(28,17±0,92)mm
średnia długość fali:
dla n=3 lewo i prawo
![]()
zmienic na 24,03
![]()
- zmien na 0,58
Ostatecznie średnia długość fali elektromagnetycznej zmierzona siatką dyfrakcyjną wynosi:
λśr=(24,03±0,58)mm
średnia długość fali:
dla n=4 lewo i prawo
![]()
zmienic na19,81
![]()
- zmien na 0,41
Ostatecznie średnia długość fali elektromagnetycznej zmierzona siatką dyfrakcyjną wynosi:
λśr=(19,81±0,41)mm
średnia długość fali:
dla n=5 lewo i prawo
![]()
zmienic na 17,89
![]()
- zmien na 0,21
Ostatecznie średnia długość fali elektromagnetycznej zmierzona siatką dyfrakcyjną wynosi:
λśr=(17,89±0,26)mm
Pomiar długości fali elektromagnetycznej za pomocą Interferometru Michelsona
Poniższa tabela przedstawia wyniki pomiarów przeprowadzonych dla interferometru Michelsona, z powodu niewielkiej długości stołu pomiarowego udało nam się dokonać pomiaru dla 15 maksimów.
Michelson |
|
odleglosc |
mV |
31 |
42 |
30,5 |
32 |
30 |
42 |
29,5 |
45 |
29 |
29 |
28,5 |
41 |
28 |
48 |
27,5 |
28 |
27 |
38 |
26,5 |
47 |
26 |
29 |
25,5 |
35 |
25 |
48 |
24,5 |
37 |
24 |
32 |
23,5 |
44 |
23 |
43 |
22,5 |
29 |
22 |
42 |
21,5 |
47 |
21 |
28 |
20,5 |
41 |
20 |
48 |
19,5 |
26 |
19 |
40 |
18,5 |
50 |
18 |
29 |
17,5 |
36 |
17 |
49 |
16,5 |
36 |
16 |
36 |
15,5 |
48 |
15 |
40 |
14,5 |
29 |
14 |
44 |
13,5 |
48 |
13 |
47 |
12,5 |
28 |
12 |
43 |
11,5 |
49 |
11 |
24 |
10,5 |
40 |
10 |
50 |
9,5 |
30 |
9 |
36 |
8,5 |
45 |
8 |
39 |
7,5 |
32 |
7 |
47 |
6,5 |
43 |
6 |
28 |
5,5 |
48 |
5 |
46 |
4,5 |
21 |
4 |
45 |
3,5 |
50 |
3 |
21 |
2,5 |
43 |
2 |
50 |
1,5 |
27 |
1 |
38 |
0,5 |
55 |
Liczba pomiarów maksimów n |
Wskazania linijki l |
Wskazanie woltomierza |
Długość fali λ |
Różnica odległości między kolejnymi maksimami la |
- |
mm |
mV |
mm |
mm |
1 |
5,0 |
55 |
- |
- |
2 |
20,0 |
50 |
20,0 |
15 |
3 |
35,0 |
50 |
23,3 |
15 |
4 |
55,0 |
48 |
27,5 |
20 |
5 |
70,0 |
47 |
28,0 |
15 |
6 |
85,0 |
45 |
28,3 |
15 |
7 |
100,0 |
50 |
28,6 |
15 |
8 |
115,0 |
49 |
28,7 |
15 |
9 |
135,0 |
48 |
30,0 |
20 |
10 |
155,0 |
48 |
31,0 |
20 |
11 |
170,0 |
49 |
30,9 |
15 |
12 |
185,0 |
50 |
30,8 |
15 |
13 |
200,0 |
48 |
30,7 |
15 |
14 |
215,0 |
47 |
30,7 |
15 |
15 |
235,0 |
44 |
31,3 |
20 |
16 |
250,0 |
48 |
31,2 |
15 |
17 |
265,0 |
47 |
31,1 |
15 |
18 |
280,0 |
48 |
31,1 |
15 |
19 |
295,0 |
45 |
31,0 |
15 |
Δl=1mm
la - 16,11
Długość fali obliczamy za pomocą poniższego wzoru:
![]()
średnia długość fali:
![]()
29,19
Błąd względny obliczamy metodą pochodnej logarytmicznej:
![]()
gdzie Δn=0
ostatecznie:
![]()
zmien na 1,81
Ostatecznie średnia długość fali elektromagnetycznej zmierzona za pomocą Interferometru Michelsona wynosi:
λ=(29,19±1,81)mm
Zestawienie rezultatów pomiarów:
Interferometr Michelsona: λ=29,19±1,81 mm,
Interferometr Fabry-Perota: λ=27,39±1,71mm
Siatka dyfrakcyjna: λśr=25,68±1,25mm [mm]
Z porównania pomiarów uzyskanych tymi metodami stwierdzamy iż, najdokładniejszą metodą pomiarową do wyznaczania długości fali jest pomiar Interferometrem Michelsona.
Najmniej dokładną zaś metodą okazał się pomiar z siatką dyfrakcyjną. Na błędy w obliczeniach pomiarów miały wpływ:
Siatki dyfrakcyjnej - niedokładność pomiaru kąta odchylenia co uwidacznia się w pomiarach widma drugiego rzędu.
Interferometrze Michelsona - niedokładność wynikająca z przesunięcia zwierciadła, oraz niedokładności odczytu.
Interferometrze Fabry-Perota - niedokładność odczytu.
![]()
Wyszukiwarka