Zestaw zadań i ćwiczeń

ze statystyki

dla klas I - III gimnazjum

CZĘŚĆ I

Odczytywanie Informacji

z Wykresów

Beata Bojarczyk

Agnieszka Brzozowska

Zadanie 1

Poniższy wykres przedstawia średnie ocen uzyskane przez uczniów pewnej klasy na koniec pierwszego półrocza.

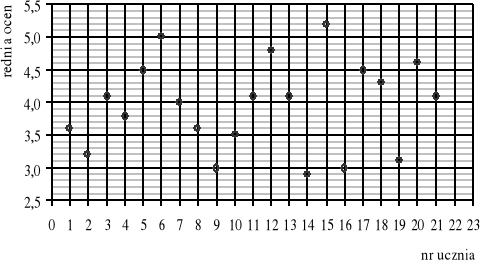
1. Ilu uczniów liczy ta klasa?

2. Jaką średnią ocen ma uczeń o numerze 7?

3. Którzy uczniowie mają średnią 4,5?

4. Jaka jest najwyższa, a jaka najniższa średnia ocen w tej klasie?

5. Jaka średnia powtarza się najczęściej?

6. Ilu uczniów uzyskało średnią wyższą niż 4,75?

Zadanie 2

Wykres punktowy przedstawia wyniki sprawdzianu z matematyki w pewnej klasie.

			•
		•	•
		•	•	•
	•	•	•	•
	•	•	•	•
•	•	•	•	•
•	•	•	•	•	•
ndst	dop	dst	db	bdb	cel

Odpowiedz na pytania i wykonaj polecenia:

1. Ile osób otrzymało ocenę dobrą?

2. Jakich ocen było najmniej?

3. Jakich ocen było najwięcej?

4. Czy więcej było ocen bdb czy dostatecznych?

5. O ile więcej było ocen dobrych niż dopuszczających?

6. Ile osób pisało ten sprawdzian?

7. Kto napisał sprawdzian lepiej: chłopcy czy dziewczęta?

Zadanie 3

Zapytano 50 uczniów, jakiego języka obcego chcieliby się uczyć. Wyniki ankiety przedstawia następujący wykres punktowy.

•
•
•
•	•
•	•	•
•	•	•
•	•	•
•	•	•
•	•	•
•	•	•	•
•	•	•	•
•	•	•	•	•
•	•	•	•	•
•	•	•	•	•	•
•	•	•	•	•	•
J. ANG.	J. NIEM.	J. FRANC.	J. WŁOSKI	J. ROSYJ.	J. HISZP.

Na podstawie wykresu sporządź diagram kołowy procentowy.

Zadanie 4

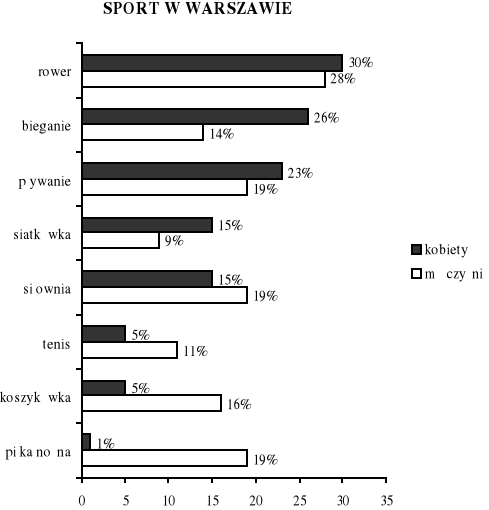
Dany jest wykres słupkowy obrazujący zainteresowanie sportem mieszkańców Warszawy.

Odpowiedz na pytania:

1. Jaki sport najbardziej lubią mężczyźni, a jaki kobiety?

2. Jaki sport cieszy się najmniejszą popularnością wśród kobiet, a jaki wśród mężczyzn?

3. Czy bieganie jest bardziej popularne wśród kobiet czy wśród mężczyzn?

4. Czy kobiety bardziej lubią pływanie czy jazdę rowerem?

5. Czy tenis jest dyscypliną bardziej popularną wśród mężczyzn niż koszykówka?

6. Ile kobiet interesuje się siatkówką?

7. Ilu mężczyzn interesuje się piłką nożną?

8. Czy są kobiety, które interesują się kilkoma dyscyplinami sportu?

9. Przez ile godzin dziennie ankietowani mężczyźni jeżdżą na rowerze?

10. Jakie inne pytania można zadać do danego wykresu? (propozycje uczniów)

11. Czy potrafisz sporządzić diagram kołowy obrazujący dyscypliny sportu uprawiane przez mężczyzn?

Zadanie 5

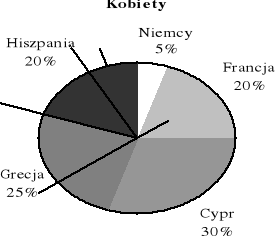
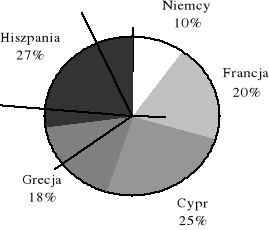
Przepytano 200 losowo wybranych przechodniów pytając, który z krajów europejskich odwiedziliby najchętniej w czasie wakacji. Uzyskane odpowiedzi ilustruje diagram.

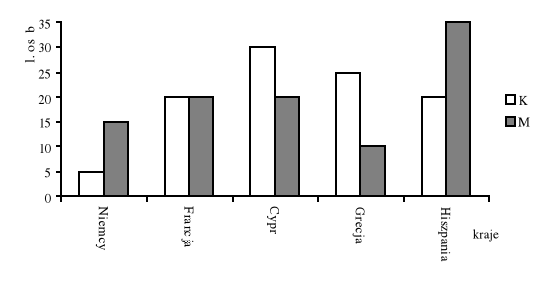
Odczytując informacje z wykresu, odpowiedz na pytania:

1. Który z krajów byłby najchętniej odwiedzany przez kobiety, a który przez mężczyzn?

2. Który z krajów cieszy się takim samym zainteresowaniem wśród kobiet i mężczyzn?

3. Który kraj cieszy się najmniejszą popularnością wśród kobiet? Jaki to % wszystkich kobiet?

4. Który kraj cieszy się najmniejszą popularnością wśród mężczyzn? Jaka to część tej grupy?

5. Z histogramu przejdź do procentowego diagramu kołowego dla grupy kobiet i mężczyzn oddzielnie.

6. Narysuj procentowy diagram kołowy dla całej 200-osobowej grupy.

Zadanie 6

Na poniższym histogramie przedstawiono absencję w dwóch równoległych klasach.

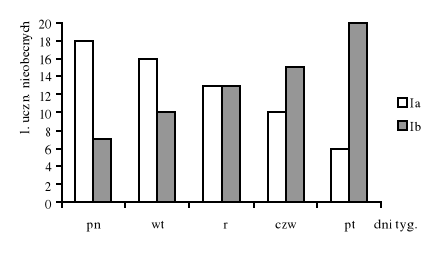
Korzystając z wykresu, odpowiedz na poniższe pytania:

1. Która klasa została wcześniej zarażona grypą?

2. Którego dnia była jednakowa absencja w obu klasach, a kiedy najbardziej się różniła?

3. Ilu uczniów brakowało w dniu o najmniejszej absencji w klasie I a? Wiedząc, że klasa I a liczy 25 uczniów, oblicz jaki to procent całej klasy.

4. Ilu uczniów brakowało w dniu o największej absencji w klasie I b? Wiedząc, że klasa I b liczy 32 uczniów, oblicz jaki to procent całej klasy.

5. Przez ile dni w klasie I a brakowało więcej niż 10 uczniów? Jaka to część „szkolnego” tygodnia? Jaki to procent?

6. Czy zauważasz tendencje zmian absencji w jednej i drugiej klasie?

Jeżeli tak to omów je.

Zadanie 7

Wyniki wagi poszczególnych uczniów pewnej klasy przedstawiono na histogramie.

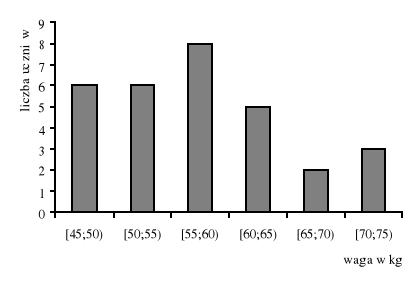
Odpowiedz na pytania:

1. Ilu uczniów liczy ta klasa?

2. Ilu uczniów waży poniżej 50 kg?

3. Ilu uczniów waży poniżej 60 kg?

4. Czy istnieją uczniowie, którzy ważą tyle samo?

5. Jaka waga dominuje w tej klasie?

6. Ilu uczniów waży dokładnie 75 kg?

7. Ilu uczniów waży co najmniej 65 kg?

8. Czy uczniowie o wadze mieszczącej się w przedziale dominującym stanowią więcej niż ¼ wszystkich uczniów tej klasy?

Zadanie 8

Na poniższym wykresie przedstawiono informacje dotyczące liczby dziewcząt w szkołach ponadpodstawowych w pewnym mieście. Łączna liczba dziewcząt wynosi 1200.

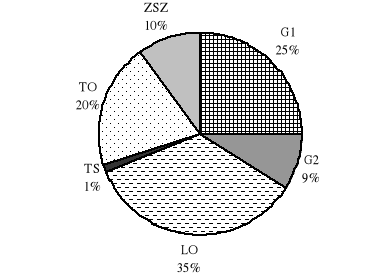
a) Odczytaj z diagramu:

1. W której szkole uczy się najwięcej dziewcząt?

2. W której szkole uczy się najmniej dziewcząt?

3. Czy gimnazjalistki stanowią więcej czy mniej niż połowę dziewcząt uczących się w szkołach ponadpodstawowych?

4. Czy w Technikum Odzieżowym uczy się więcej dziewcząt niż w Gimnazjum nr 2?

5. Jakie inne informacje możesz odczytać z wykresu?

2. Korzystając z danych, oblicz ilość (częstość) dziewcząt uczących się w poszczególnych szkołach.

3. Uzyskane w zadaniu b) wyniki przedstaw w postaci tabeli częstości.

Zadanie 9

Dany jest wykres przedstawiający bezrobotnych wg wykształcenia w woj. podlaskim na koniec 2000 r.

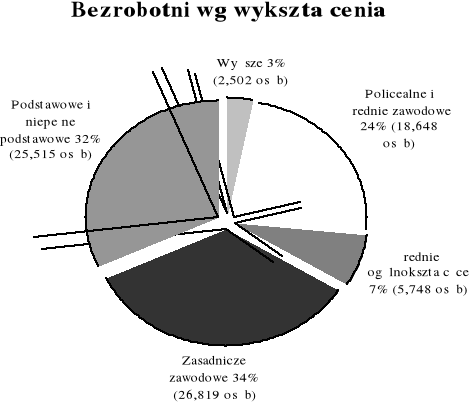
Odpowiedz na pytania:

1. Czy z wykresu wynikają informacje dotyczące wieku bezrobotnych?

2. Uporządkuj w kolejności rosnącej bezrobotnych odczytując dane z diagramu.

3. Czy z powyższego wykresu wynika fakt, że im wyższy poziom wykształcenia, tym łatwiej zdobyć pracę?

4. Ilu bezrobotnych było w woj. podlaskim na koniec roku 2000?

5. Czy bezrobotni z wykształceniem wyższym, policealnym i średnim zawodowym oraz średnim ogólnokształcącym stanowią więcej niż połowę wszystkich bezrobotnych?

6. W którym z miast woj. podlaskiego najgorzej wygląda rynek pracy?

7. Jak wysokie jest bezrobocie w samym Białymstoku?

8. Jaki zawód stwarza największe szanse na zatrudnienie?

Zadanie 10

Na podstawie diagramu odpowiedz na pytania:

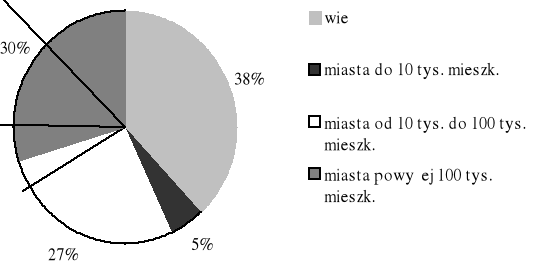
1. Jaki procent osób mieszka w miastach do 10 tys. mieszkańców?

2. Czy więcej osób mieszka na wsi czy w mieście?

3. Czy na wsi mieszka więcej czy mniej niż 1/3 ludności kraju?

4. Jaki procent osób mieszka w miastach poniżej 100 tys. mieszkańców?

Zadanie 11

Liczba mieszkań przeznaczonych na sprzedaż lub wynajem w latach 1994—1997 wynosiła 12 200.

Niżej przedstawiono diagram kołowy liczb tych mieszkań w poszczególnych latach. Wyznacz liczbę mieszkań przeznaczonych na sprzedaż lub wynajem w roku: 1994, 1995, 1996 i 1997.

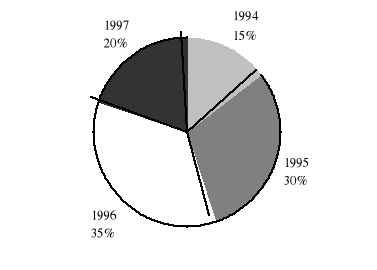
Odpowiedz na pytania:

1. O ile mieszkań więcej sprzedano lub wynajęto w roku 1996 niż w 1994?

2. Czy w latach 1994 i 1995 sprzedano lub wynajęto mniej mieszkań niż 1996?

3. Ile mieszkań sprzedano w 1998 roku?

4. O ile spadła ilość sprzedanych lub wynajętych w 1997 roku w stosunku do roku 1996?

Zadanie 12

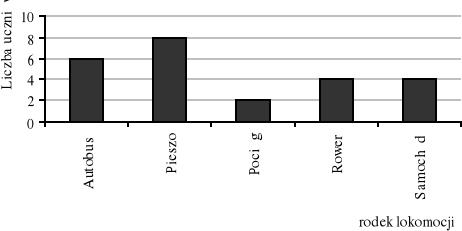
Poniższy wykres kołowy przedstawia wyniki badań na temat środków lokomocji, jakimi uczniowie kl. I dotarli w pewnym dniu do szkoły.

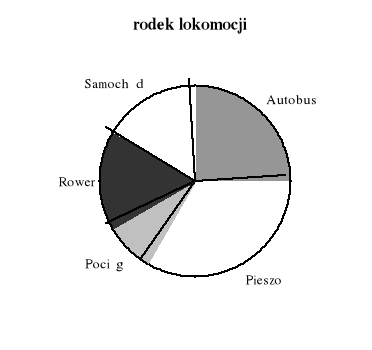
Wykonując odpowiednie obliczenia uzupełnij tabelę częstości:

Środek lokomocji	Liczba uczniów
Autobus Pieszo Pociąg Rower Samochód
Razem	24

Odpowiedz na pytania:

1. Który środek lokomocji jest najbardziej popularny wśród uczniów tej klasy?

2. Czy dojazd rowerem jest bardziej popularny niż autobusem?

3. O ile osób więcej przyjechało autobusem niż pociągiem?

4. Ile osób przyjechało tramwajem?

Wykorzystując uzupełnioną tabelę sporządź histogram.

Zadanie 13

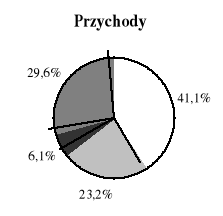
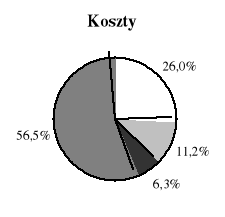
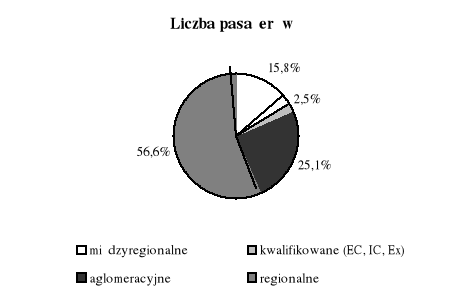
Diagramy przedstawiają jaka część pasażerów, jaka część przychodów i jaka część kosztów przewozów pasażerskich PKP w roku 1999 przypadała na poszczególne rodzaje pociągów.

Korzystając z diagramów odpowiedz na poniższe pytania:

PKP w 1999 roku

1. Jaka część kosztów przypadała na pociągi aglomeracyjne?

2. Jaka część pasażerów przejechała pociągami regionalnymi?

3. Którym z rodzajów pociągów przejechała więcej niż połowa wszystkich pasażerów?

4. Pociągami kwalifikowanymi przejechało zaledwie 2,5 % pasażerów, a i tak dało to kolei ponad 20 % przychodów. Dlaczego?

5. Który z rodzajów pociągów był najbardziej opłacalny dla kolei?

6. Wymyśl 3 inne podobne pytania i odpowiedz na nie.

Zadanie 14

Na wykresach podano liczbę ludności kilku miast w różnych latach.

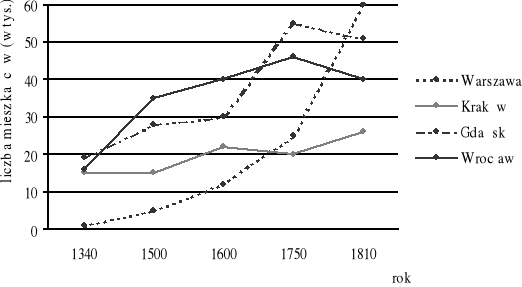
a) W którym roku Wrocław miał największą liczbę mieszkańców?

2. O ilu więcej mieszkańców miał Gdańsk od Wrocławia w roku 1600?

3. W którym z miast między rokiem 1750 a 1810 liczba ludności rosła najszybciej?

4. Porównaj zmiany liczby ludności Krakowa i Warszawy w okresie od roku 1600 do 1750. Czy domyślasz się, skąd wynikały te zmiany?

Zadanie 15

Wykres przedstawia cenę akcji (w zł) firmy Zysk & Ryzyko w kolejnych dniach lutego pewnego roku.

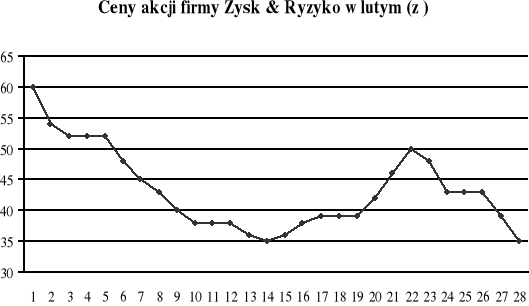
1. O ile złotych spadła w lutym wartość tych akcji?

2. Czy kupując i sprzedając te akcje w ciągu lutego, można było na nich zarobić? W jakich dniach należało je kupować, a w jakich sprzedawać, aby zysk w ciągu lutego był możliwie największy?

3. W soboty i niedziele giełda jest nieczynna. Czy domyślasz się, w których dniach lutego tamtego roku były poniedziałki?

Zadanie 16

Na poniższym rysunku przedstawione są wykresy zmiany temperatury odnotowanej tego samego dnia w Białymstoku i Szczecinie.

a) Jaką temperaturę pokazywał termometr w obu miastach o 12⁰⁰?

2. O której godzinie temperatura w tych miastach wynosiła 0^oC?

3. W jakich godzinach temperatura w Białymstoku była ujemna?

4. O której godzinie temperatura w obu miastach była taka sama?

5. W jakich godzinach w Białymstoku było cieplej niż w Szczecinie?

6. Jaka była najwyższa temperatura w Białymstoku, a jaka w Szczecinie? O której to było godzinie?

7. Jaka temperatura była w Białymstoku, gdy w Szczecinie było 3^oC?

Odpowiedzi do zadań

i komentarz metodyczny

Zadanie 1

1. Klasa liczy 21 uczniów.

2. Uczeń o numerze 7 ma średnią ocen równą 4,0.

3. Średnią 4,5 mają uczniowie o numerach 5 i 17.

4. Najwyższa średnia ocen w klasie: 5,2; a najniższa: 2,9.

5. Najczęściej powtarza się średnia 4,1.

6. Średnią wyższą niż 4,75 uzyskało trzech uczniów.

Zadanie 2

1. Ocenę dobrą otrzymało 7 osób.

2. Najmniej było ocen celujących.

3. Najwięcej było ocen dobrych.

4. Ocen dostatecznych było więcej niż bardzo dobrych.

5. Ocen dobrych było o 3 więcej niż dopuszczających.

6. Sprawdzian pisało 25 osób.

7. Nie wiemy.

Zadanie 4

1. Mężczyźni i kobiety najbardziej lubią jazdę na rowerze.

2. Najmniejszą popularnością wśród kobiet cieszy się piłka nożna, a wśród mężczyzn -siatkówka.

3. Bieganie jest bardziej popularne wśród kobiet.

4. Kobiety bardziej lubią jazdę rowerem.

5. Bardziej popularna jest koszykówka.

6. Nie wiemy.

7. Nie wiemy.

8. Tak.

9. Nie wiemy.

10. Propozycje uczniów.

11. Nie.

Zadanie 5

1. Kobiety najchętniej odwiedzają Cypr, a mężczyźni Hiszpanię.

2. Takim samym zainteresowaniem wśród kobiet i mężczyzn cieszy się Francja.

3. Najmniejszą popularnością wśród kobiet cieszą się Niemcy. Jest to 5% wszystkich kobiet.

4. Najmniejszą popularnością wśród mężczyzn cieszy się Grecja. Jest to 0,1 grupy mężczyzn.




Zadanie 6

1. Wcześniej zarażona grypą została klasa I a.

2. Jednakowa absencja w obu klasach była we środę, a najbardziej się różniła w piątek.

3. W piątek brakowało 6 uczniów klasy I a, co stanowi 24% uczniów tej klasy.

4. W piątek brakowało 20 uczniów klasy I b, co stanowi 62,5% całej klasy.

5. Więcej niż 10 uczniów brakowało w klasie I a przez 3 dni, co stanowi 3/5 czyli 60% szkolnego tygodnia.

6. W klasie I a zauważam tendencję spadkową, a w klasie I b - wzrostową.

Zadanie 7

1. Klasa liczy 30 uczniów.

2. Poniżej 50 kg waży 6 uczniów.

3. Poniżej 60 kg waży 20 uczniów.

4. Nie wiemy.

5. Nie wiemy - przedział dominujący [55;60).

6. Nie wiemy.

7. Co najmniej 65 kg waży 5 uczniów.

8. 8/30 = 16/60 > 15/60 = 1/4.

Uczniowie o wadze mieszczącej się w przedziale dominującym stanowią więcej niż 1/4 klasy.

Zadanie 8

Odpowiedzi na pytania:

1. Najwięcej dziewcząt uczy się w Liceum Ogólnokształcącym.

2. Najmniej dziewcząt uczy się w Technikum Samochodowym.

3. Gimnazjalistki stanowią mniej niż połowę uczących się w szkołach ponadpodstawowych.

4. Tak, w Technikum Odzieżowym uczy się więcej dziewcząt niż w Gimnazjum nr 2.

b) G1 : 25% * 1200 = 300

G2 : 9% * 1200 = 108

LO : 35% * 1200 = 420

TS : 1% * 1200 = 12

TO : 20% * 1200 = 240

ZSZ : 10% * 1200 = 120

c)

Rodzaj szkoły	Liczba dziewcząt (częstości)
G1 G2 LO TS TO ZSZ	300 108 420 12 240 120
Razem	1200

Zadanie 9

1. Nie wynikają.

2. Wyższe, średnie ogólnokształcące, policealne i średnie zawodowe, podstawowe i niepełne podstawowe, zasadnicze zawodowe.

3. Tak.

4. Na koniec 2000 roku było w woj. podlaskim 79232 osoby bezrobotne.

5. Bezrobotni z podanym wykształceniem stanowią mniej niż połowę wszystkich bezrobotnych.

6. Nie wiemy.

7. Nie wiemy.

8. Nie wiemy.

Zadanie 10

1. W miastach do 10 tys. mieszka 5% Polaków.

2. Więcej osób mieszka w miastach.

3. Na wsi mieszka więcej niż 1/3 ludności kraju.

4. W miastach poniżej 100 tys. mieszkańców mieszka 32% ludności kraju.

Zadanie 11

Liczby mieszkańców:

1994r - 15% * 12200 = 1830

1995r - 30% * 12200 = 3660

1996r - 35% * 12200 = 4270

1997r - 20% * 12200 = 2440

Odpowiedzi na pytania:

1. W roku 1996 sprzedano lub wynajęto o 2440 mieszkań więcej niż w 1994 roku.

2. W 1994 i 1995 sprzedano lub wynajęto mieszkań niż w 1996 roku.

3. Nie wiemy.

4. W 1997 ilość sprzedanych lub wynajętych mieszkań zmniejszyła się w stosunku do roku 1996 o 1830 lokali.

Zadanie 12

Środek lokomocji	Liczba uczniów
Autobus Pieszo Pociąg Rower Samochód	6 8 2 4 4
Razem	24

Odpowiedzi na pytania:

1. Najwięcej uczniów tego dnia przyszło pieszo.

2. Bardziej popularny jest dojazd autobusem niż rowerem.

3. Autobusem przyjechało o 4 uczniów więcej niż pociągiem.

4. Nie wiemy.

e)




Zadanie 13

1. Na pociągi aglomeracyjne przypadało 6,3% kosztów.

2. Pociągami regionalnymi przejechało 56,6% wszystkich pasażerów.

3. Więcej niż połowa wszystkich pasażerów przejechała pociągami regionalnymi.

4. Mimo małej ilości pasażerów kolei zyskała 20% przychodów z powodu wysokich cen biletów na pociągi kwalifikowane.

5. Wskazówka. Oblicz stosunek przychodów do kosztów dla każdego rodzaju pociągu.

p. międzyregionalne = 41,1% / 26% = 1,58

p. kwalifikowane = 23,2% / 11,2% = 2,07

p. aglomeracyjne = 6,1% / 6,3% = 0,97

p. regionalne = 29,6% / 56% = 0,52

Najbardziej opłacalne dla kolei są pociągi kwalifikowane.

6. Propozycje uczniów.

Zadanie 14

1. Wrocław miał największą liczbę mieszkańców w 1750 roku.

2. W 1600 roku Gdańsk miał o 15 tys. mieszkańców więcej niż Wrocław.

3. W latach 1750 - 1810 najszybciej liczba ludności rosła w Warszawie.

4. W okresie 1600 - 1750 roku liczba mieszkańców Krakowa zmalała, a Warszawy wzrosła.

Zmiany te wynikają z faktu przeniesienia stolicy z Krakowa do Warszawy.

Zadanie 15

1. Wartość akcja spadła w lutym o 25 zł.

2. Kupując i sprzedając akcje w ciągu lutego można było na nich zarobić. Aby zysk możliwie największy (15 zł za akcję) należało kupić akcje 14 lutego, a sprzedać 22 lutego.

3. Poniedziałki były: 5, 12, 19, 26 lutego.

Zadanie 16

1. O godzinie 12⁰⁰ w Szczecinie były 2^oC, a w Białymstoku 1^oC.

2. 0^oC w Białymstoku było o godz. 11⁰⁰, a w Szczecinie o 10⁰⁰.

3. W Białymstoku temperatura była w godz. 0⁰⁰ - 11⁰⁰.

4. Temperatura w obu miastach była taka sama o godz. 13⁰⁰ i 21⁰⁰.

5. W Białymstoku było cieplej niż w Szczecinie w godz. 13⁰⁰ - 21⁰⁰.

6. Najwyższa temperatura w Białymstoku wynosiła 5^oC (godz. 16⁰⁰), a w Szczecinie 4^oC (również o godz. 16⁰⁰).

7. Gdy w Szczecinie było 3^oC, to w Białymstoku było 4^oC.

Komentarz

Zadania 1, 2, 3 kształtują umiejętność odczytywania informacji z wykresów punktowych.

Zadania 4, 5, 6, 7 dotyczą histogramu. Mają na celu sprawdzenie, czy uczniowie potrafią prawidłowo odczytywać informacje przedstawione za pomocą diagramu słupkowego.

Zadanie 5 kształtuje umiejętność przejścia od histogramu do diagramu kołowego.

Zadania 8 - 13 dotyczą diagramów kołowych. Uczniowie wykonując odpowiednie obliczenia muszą odpowiedzieć na podane pytania i formułować własne wnioski.

Zadania 14 - 16 służą sprawdzeniu czy uczniowie potrafią odczytywać informacje przedstawione w postaci wykresów liniowych.

18

---