Katedra Konstrukcji Stalowych

Kierunek Budownictwo-studia dzienne

Wydział Budownictwa Architektury przedmiot: Konstrukcje metalowe

i Inżynierii Środowiska rok 2008/2009

sem. IV

Ćwiczenie projektowe z konstrukcji stalowych nr.2

Wykonawca:

Krzysztof Kurzaj

Osoba prowadząca:

mgr inż. Michał Gajdzicki

Data oddania:

Łódź, czerwiec 2009

I. Dane do projektu:

Rozpiętość podciągu: L=12,9m

Rozstaw podciągów: B=8,7m

Ciężar warstw wykończeniowych:

Obciążenie użytkowe stropu:

Stal gatunku: S235

Przyjęto rozstaw osiowy belek równy: b = 2 m

Przyjęto belkę o przekroju dwuteowym IPE 330 o następującej specyfikacji:

wysokość przekroju gałęzi h=330mm

szerokość stopki b=160mm

grubość stopki
=11,5mm

grubość środnika
=7,5mm

promień zaokrąglenia R=18mm

pole przekroju: A=62,6 cm²

masa: m=49,1 kg/m
momenty bezwładności: I_y=11770 cm⁴
I_z=788 cm⁴
wskaźnik wytrzymałości: W_y=713 cm³
W_z=98,5 cm³
promień bezwładności: i_y=13,7 cm
i_z=3,55 cm

rozpiętość belki L=8700mm

granica plastyczności fy=235N/mm²

moduł sprężystości E=210000N/mm²

wskaźnik sprężysty W_el,y=W_y

W_el,z=W_z

Wskaźnik plastyczny W_pl,y=804,33 cm³

1. Zebranie obciążeń.

a) dla belek środkowych:

Obciążenie stałe:

-płyta żelbetowa grubości 10cm:

-ciężar warstw wykończeniowych:

-ciężar własny belki IPE 330

Obciążenie użytkowe:

Wartości obliczeniowe: Q = 1,35*6,18 kN/m + 1,5*5kN/m =15,84 kN/m

b) dla pierwszej i ostatniej belki:

Obciążenie stałe:

-płyta żelbetowa grubości 10cm:

-ciężar warstw wykończeniowych:

-ciężar własny belki IPE 330

Obciążenie użytkowe:

Wartości obliczeniowe: Q = 1,35*4,613 kN/m + 1,5*3,625kN/m =11,67 kN/m

2. Obliczenia statyczne belki stropowej.

a) dla belek środkowych:

M_Ed = 149,87 kNm
V_Ed = 68,90kN
R = 68,90kN

b) dla pierwszej i ostatniej belki:

M_Ed = 110,41 kNm
V_Ed = 50,76kN
R₁ = 50,76kN

3.Wymiarowanie belki stropowej.

3.1. Sprawdzenie stanu granicznego nośności belki stropowej z dwuteownika walcowanego

3.1.1. Klasa przekroju przy zginaniu względem osi y-y,

Współczynnik:

Stosunek szerokości grubości:

- środnika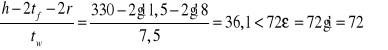

- stopki

Środnik przy równomiernym ściskaniu jest klasy 1, pas klasy 1, a więc

przekrój jest klasy 1

3.1.2. Nośność obliczeniowa przekroju klasy 1 przy zginaniu.

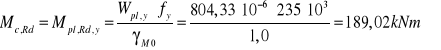
Rozkład momentu zginającego siły tnącej jest taki, że można nie brać pod uwagę wpływu siły poprzecznej na nośność przekroju przy zginaniu.

Współczynnik zwichrzenia:

Belka jest zespolona z płytą, a więc nie występuje zwichrzenie:

Nośność belki na zwichrzenie

Sprawdzenie nośności belki ze względu na zwichrzenia

Warunek spełniony

3.1.3. Sprawdzenie nośności belki przy zginaniu w prześle,

Warunek spełniony

3.1.4. Sprawdzenie nośności belki przy ścinaniu na podporze :

Warunek stateczności miejscowej przy ścinaniu:

Środnik nie jest wrażliwy na utratę stateczności przy ścinaniu

Pole przekroju czynnego

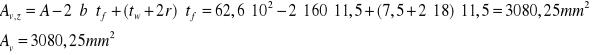
Lecz nie mniej niż

Przyjęto:
=1,2

Obliczeniowa nośność przekroju przy ścinaniu

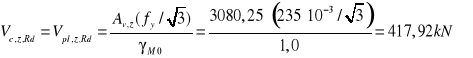
Nośność przy podporze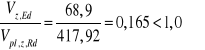

Warunek spełniony

3.2. Sprawdzenie stany granicznego użytkowalności.

Kombinacja obciążeń

Maksymalne ugięcie belki

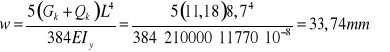
Wartość ugięcia pionowego belki głównej nie powinna przekraczać wartości granicznej wynoszącej:

Warunek spełniony.

4. Obliczenia statyczne podciągu.

2R=2*68,9kN=137,8kN

2R₁ =2* 50,76kN=101,52kN

Przyjęto podciąg o przekroju dwuteowym spawanym o następującej specyfikacji:

wysokość przekroju gałęzi h=1100mm

szerokość stopki b=250mm

grubość stopki
=20mm

grubość środnika
=8mm

masa: m=145,1kg/m

pole przekroju: A= 184.8cm²
momenty bezwładności: I_y= 371034.4cm⁴
I_z= 5212.856cm⁴

rozpiętość podciągu L=12900mm

granica plastyczności fy=235N/mm²

moduł sprężystości E=210000N/mm²

Ciężar własny dwuteownika :

M_Ed = 1470,45 kNm
V_Ed = 455,18kN
R = 455,18kN

5. Wymiarowanie podciągu.

5.1. Sprawdzenie stanu granicznego nośności podciągu spawanego, stężonego bocznie punktowo w przekroju przęsłowym i podporowym.

5.1.1. Klasa przekroju przy zginaniu,

Współczynnik:

Stosunek szerokości grubości:

- środnika

- stopki

Środnik przy równomiernym ściskaniu jest klasy 4, pas klasy 1

Przy zginaniu względem osi y-y przekrój jest klasy 4, przy czym tylko środnik jest wrażliwy na utratę stateczności miejscowej. Sprawdzenie klasy wykonano przy rozkładzie naprężeń normalnych przekroju brutto (
). Przy redukcji pola przekroju wywołanej utratą stateczności miejscowej i zmianą położenia środka ciężkości pozostanie klasa 4 ( zakres strefy ściskanej środnika
)

5.1.2. Nośność obliczeniowa przekroju klasy 4 przy zginaniu,

Stateczność miejscowa środnika

Parametr niestateczności zginanej ścianki usztywnionej przy współczynniku rozkładu naprężeń

Smukłość płytowa ścianki:

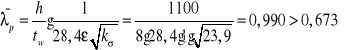
Współczynnik redukcyjny:

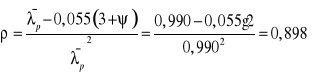
Szerokość strefy ściskanej i rozciąganej środnika (
)

Szerokość współpracująca:

Szerokość części przylegających do pasa ściskanego
i do osi obojętnej

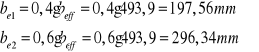
Przesunięcie położenia osi obojętnej przekroju współpracującego

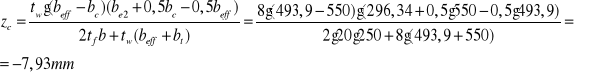
Moment bezwładności przekroju współpracującego:

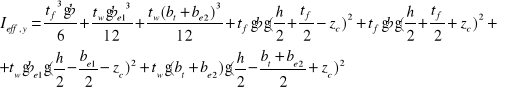
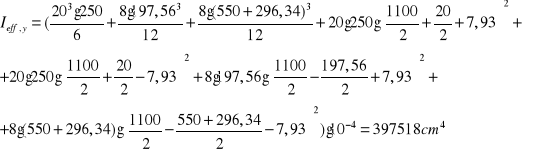
Wskaźnik sprężysty skrajnych włókien ściskanych przekroju współpracującego:

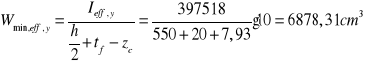
Wskaźnik sprężysty skrajnych włókien rozciąganych przekroju współpracującego:

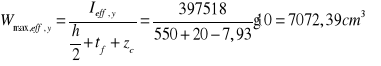
Nośność obliczeniowa przekroju klasy 4 przy zginaniu względem osi y-y:

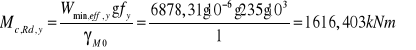
5.1.3.Uproszczona ocena zwichrzenia w budynkach,

Belki, których pas ściskany jest stabilizowany punktowo w kierunku bocznym stężeniami o rozstawie Lc nie są narażone na zwichrzenie, jeśli spełniony jest warunek:

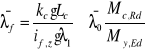
Gdzie:

- maksymalny obliczeniowy moment miedzy stężeniami,

- współczynnik poprawkowy,

- promień bezwładności pasa zastępczego, składającego się z pasa ściskanego i 1/3 ściskanej części środnika, względem osi z-z przekroju,

- smukłość graniczna pasa zastępczego:

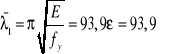
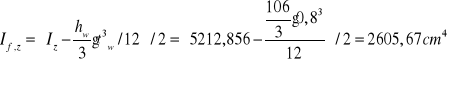
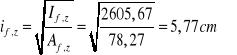
Rozkład momentu zginającego w przęśle między stężeniami jest bliski stałemu , tym samym można przyjąć:

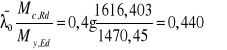
warunek spełniony.

5.1.4.Sprawdzenie nośności podciągu przy zginaniu w przęśle,

warunek spełniony.

5.1.5.Sprawdzenie nośności podciągu przy ścinaniu na podporze,

Warunek stateczności miejscowej przy ścinaniu:

Środnik nie spełnia warunków stateczności przy ścinaniu, zatem konieczne jest jego usztywnienie żebrami poprzecznymi co najmniej na podporach.

Niestateczność środka przy ścinaniu:

Względna smukłość płytowa:

Współczynnik niestateczności przy ścinaniu:

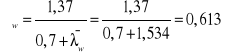
gdy:

Nośność obliczeniowa przekroju przy ścinaniu:

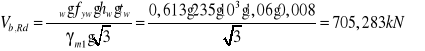
W obliczeniach pominięto udział pasów w nośności obliczeniowej przy ścinaniu.

Warunek nośności przy ścinaniu:

warunek spełniony.

5.2. Sprawdzenie stanu granicznego użytkowalności:

Ugięcie belki całkowite:

Wartość ugięcia pionowego belki głównej nie powinna przekraczać wartości granicznej wynoszącej:

Warunek spełniony.

5.3. Sprawdzenie nośności spoin pachwinowych łączących pas ze środnikiem w strefie przypodporowej.

Współczynniki :

Grubość spoiny pachwinowej a=5mm

Warunek nośności dla spoin pachwinowych:

Naprężenia normalne prostopadłe do przekroju spoin:

Naprężenia styczne prostopadłe do przekroju spoin:

Naprężenia styczne równoległe do spoiny:

455,18kN

Sprawdzenie warunku nośności dla spoin:

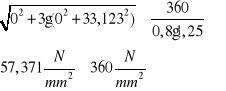
Warunek spełniony.

5.4. Dobór przekroju żebra w miejscu połączenia belek stropowych z podciągiem.

Przyjęto żebro o grubości
, szerokości
, wysokości

6. Wymiarowanie połączenia belki stropowej z podciągiem.

Połączenie zakładkowe typu dociskowego- kategoria A.

Parametry śruby M16 klasy 6,8

Średnica: d=16mm

Otwór:
=17mm

Pole przekroju czynnego:

Granica plastyczności:

Wytrzymałość na rozciąganie:

Grubość płaskownika: t= 10,0mm

a) Obliczenie nośności śrub na ścinanie w jednej płaszczyźnie:

Założono że płaszczyzna ścinania przechodzi przez gwintowaną część śruby

Dlas klasy 6,8

Obliczeniowa nośność pojedynczej śruby na ścinanie

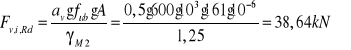
Obliczeniowa nośność grupy śrub na ścinanie

b) Obliczeniowa nośność śrub na docisk:

Odległość od osi śruby skrajnej do krawędzi czołowej:

Rozstaw śrub w szeregu:

Odległość od śruby skrajnej do krawędzi bocznej:

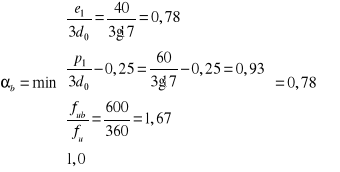
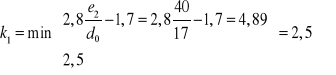
Obliczeniowa nośność pojedynczej śruby na docisk:

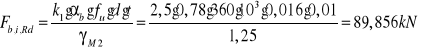
Obliczeniowa nośność grupy sił na docisk:

Warunek nośności połączenia:

Warunek jest spełniony

---