Wstęp teoretyczny

W procesach chemicznych często wykorzystuje się reaktory z wypełnieniem. Mogą być to dowolne cząsteczki o małych rozmiarach, np. immobilizowane enzymy. Zadaniem upakowanego złoża jest poprawienie kontaktu między dwoma substancjami znajdującymi się w reaktorze. Reaktory te są rurowe i wypełnione stałymi cząsteczkami katalizatora - najczęściej są używane w celu przyśpieszania reakcji gazowych. Reakcja chemiczna zachodzi na powierzchni katalizatora.

Zaletami wykorzystywania reaktorów ze złożem upakowanym są: wyższa konwersja substancji w przeliczeniu na masę katalizatora niż w innych reaktorach, niskie koszty operacyjne i możliwość przeprowadzania procesu ciągłego. Dodatkowo, szybkość reakcji zależy od ilości katalizatora, a nie objętości reaktora.

Wady: stosunkowo duże spadki ciśnienia przy przepływach mieszanin gazowych, gradienty temperaturowe, ograniczona możliwość kontroli temperatury.

W przemyśle wykorzystuje się kolumny z wypełnieniem w procesach separacji, takich jak absorpcja i destylacja. Kolumna z wypełnieniem jest podłużnym zbiornikiem ciśnieniowym, w którym znajduje się upakowane złoże. Ciecze mają tendencję do zwilżania powierzchni tego złoża, w następstwie czego następuje transfer masy. W celu poprawy separacji w kolumnach destylacyjnych wykorzystuje się złoże upakowane zamiast półek - poprawia to wydajność procesu. Innymi czynnikami wpływającymi na wydajność są kształt i powierzchnia upakowanego złoża oraz pary i ciecz wnikające do złoża.

Kolumny upakowane mają ciągłą krzywą równowagi pary, w przeciwieństwie do konwencjonalnych półek teoretycznych, gdzie każda półka stanowi oddzielny punkt równowagi para-ciecz. Jakkolwiek, użytecznym jest policzenie liczby półek teoretycznych w celu określenia skuteczności separacji upakowanej kolumny. Najpierw określa się liczbę niezbędnych teoretycznych etapów równowagi, a następnie wysokość upakowania, równą teoretycznemu stadium równowagi, zwaną też wysokością równą półce teoretycznej (HETP). Całkowita wysokość wymaganego złoża to liczba teoretycznych etapów, pomnożona przez HETP.

W doświadczeniu wykorzystano izomerazę glukozową, przeprowadzającą reakcję izomeryzacji D-glukozy do D-fruktozy. Enzym do aktywności wymaga między innymi jonów Co²⁺ i Mg²⁺. Reakcja jest równowagowa, izomeraza wykazuje powinowactwo zarówno do substratu (glukozy) jak i produktu (fruktozy). Podczas wyznaczania parametrów kinetycznych, szybkość reakcji w różnych stężeniach substratu mierzy się w warunkach początkowych, a więc zanim stopień przereagowania przekroczy 3%. Przy założeniu, że część enzymu nie jest dostępna dla substratu z racji obecności produktu w mieszaninie reakcyjnej, szybkość reakcji izomeryzacji można policzyć modelem wynikającym z inhibicji kompetycyjnej (jest to różnica między szybkością reakcji GF a FG).

Źródła

• Instrukcja „Reaktory przepływowe - kolumna ze złożem upakowanym” do wykonania ćwiczenia (Politechnika Wrocławska)

• A.Jaworek, T.Czech, A.Krupa, T.Antes, „Kierunki rozwoju elektrostatycznych urządzeń do oczyszczania gazów odlotowych”, V Konferencja Naukowo-Techniczna ELEKTROFILTRY'2000, Kraków 14-16 września 2000, 59-68

• http://www.engin.umich.edu/~cre/asyLearn/bits/pbr/index.htm

• http://pubserv.uprp.pl/PublicationServer/Temp/e78279p824bhlpn6acb94vs612/PL113309B2.pdf (opis patentowy unieruchamiania izomerazy glukozowej)

Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z procedurą postępowania przy wyznaczaniu stałych równania kinetycznego reakcji równowagowej izomeryzacji D-glukozy do D-fruktozy oraz prowadzenie procesu w kolumnie ze złożem upakowanym z immobilizowaną izomerazą glukozową.

Materiały i metody

- immobilizowana izomeraza glukozowa (ksylozowa) otrzymana nieodpłatnie od firmy Novozyme

- 0.05 M bufor Tris-HCl + 3mmol Mg, ph 7.8 w 40 st.C

- odczynniki do enzymatycznego oznaczania stężenia glukozy

- spektrofotometr UV-VIS Shimadzu

- termostatowane reaktory kolumnowe

- pompy tłokowe Prominent

- roztwory glukozy i fruktozy

* objętość całkowita złoża - 18,5 ml

* objętość wolna reaktora - 6,29 ml

* temperatura procesu: 40 st.C

Wykonanie doświadczenia

Pomiar zmiany stężeń reagentów w warunkach początkowej szybkości reakcji: Przygotowano roztwory glukozy i fruktozy o zadanych stężeniach w zakresie od 50 do 1750 mM, odważając odpowiednią ilość glukozy i fruktozy i dopełniając buforem do 500 cm³. Roztwory dokładnie wymieszano aż do całkowitego rozpuszczenia się kryształów. Do termostatowanych (40 st.C) reaktorów kolumnowych ze złożem upakowanym dozowano substrat z podanymi szybkościami przepływu (pompa „mała” - 60/120; 40/120; 20/120; 10/120; pompa „duża” - 15/120; 7,5/120; 2,5/120; 0/120), jednocześnie mierząc strumień przepływu (pomiar czasu napełniania cylindra na 50 cm³). Pobrano próbki do dalszej analizy.

Oznaczanie stężenia glukozy testem enzymatycznym: do suchych i czystych probówek wprowadzono po 1 cm³ roztworu roboczego, przygotowano również 2 probówki na standard glukozy i próbę kontrolną. Z próbek pobierano po 10 μl i dodawano do probówek z roztworem roboczym, dokładnie przepłukując końcówki. Roztwory wstawiono do łaźni wodnej ustawionej na 37 st.C na 5 minut, a następnie zmierzono absorbancję przy 500 nm wobec próby kontrolnej. Jako wartość absorbancji dla standardu glukozy przyjęto 15 mM i dalsze obliczenia wykonano z proporcji. Przy stosowaniu glukozy jako substratu, pobranych próbek nie rozcieńczano, natomiast przy wykorzystaniu jako substrat glukozy wykonano rozcieńczenia zgodnie z danymi podanymi w tabeli poniżej.

Wyznaczanie wartości K_eq reakcji izomeryzacji: Do probówki wprowadzono 5 cm³ 0.05 M roztworu glukozy i dodano 50 μl natywnej izomerazy glukozowej. Wstawiono do łaźni wodnej ustawionej na temperaturę 40 st.C. Odczekano w celu osiągnięcia przez układ równowagi termodynamicznej.

Stężenie glukozy [mM]	Rozcieńczenie [-]	Objętość roztworu badanego [l]	Objętość wody [ml]
50	2x	1000	1
100	3x	1000	2
200	10x	1000	9
400	20x	500	9,5
600	20x	500	9,5
800	40x	250	9,75
1000	40x	250	9,75
1250	50x	200	9,8
1500	50x	200	9,8
1750	100x	100	9,9

Reakcje izomeryzacji glukozy do fruktozy

Stężenie standardu C_st = 15 mM

Objętość próbki V_p = 50 ml

Objętość wolna reaktora V_r = 6,29 ml

Przykładowe obliczenia dla próbki nr 1

Cs = 50 mM

Abs_{śr,standardu} = 0,965

Abs_{śr,substratu} = 1,548

• Stężenie początkowe rzeczywiste substratu (glukozy):
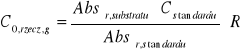
  [mM]

[mM]

• Stężenie początkowe substratu (glukozy) dla RP = 30:

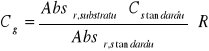
[mM]

[mM]

• Stężenie produktu (fruktozy):

[mM]
[mM]

• Strumień przepływu V:
  
  

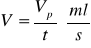
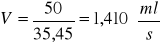
• Czas przebywania τ:
  
  

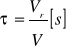
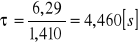
• Stopień przereagowania α:
  
  

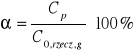
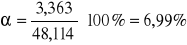
• Szybkość reakcji r:
  
  

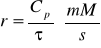
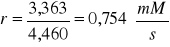
Wyniki zestawione zostały w tabelach:

RP	t [s]	średnia Abs	C0,rzecz,g [mM]	Cg [mM]	Cp [mM]	[ml/s]	 s]	α [%]	r [mM/s]
30	35,45	1,440	48,114	44,751	3,363	1,410	4,460	6,98902	0,75403
20	56,93	1,525	R=2x	47,409	0,705	0,878	7,162	1,46457	0,09839
10	80	1,516		47,140	0,974	0,625	10,064	2,02455	0,09679
0	179	1,640			50,974	-2,860	0,279	22,518	-5,94443	-0,12701

Cs = 100 mM

Abs_{śr,standardu} = 1,003

Abs_{śr,substratu} = 2,101

RP	t [s]	średnia Abs	C0,rzecz,g [mM]	Cg [mM]	Cp [mM]	[ml/s]	 s]	α [%]	r [mM/s]
30	34,71	1,820	94,263	81,671	12,592	1,441	4,367	13,35872	2,88385
20	51,73	2,056	R=3x	92,253	2,010	0,967	6,508	2,13283	0,30894
10	74	1,946		87,307	6,956	0,676	9,309	7,37920	0,74720
0	181	1,967			88,261	6,002	0,276	22,770	6,36753	0,26361

Cs = 400 mM

Abs_{śr,standardu} = 0,949

Abs_{śr,substratu} = 1,246

RP	t [s]	średnia Abs	C0,rzecz,g [mM]	Cg [mM]	Cp [mM]	[ml/s]	 s]	α [%]	r [mM/s]
80	68	1,133	394,027	358,398	35,629	0,735	8,554	9,04227	4,16499
60	86	1,242	R=20x	392,604	1,423	0,581	10,819	0,36116	0,13153
40	117	1,348		426,283	-32,256	0,427	14,719	-8,18620	-2,19150
20	273	1,281			404,989	-10,963	0,183	34,343	-2,78224	-0,31921

Cs = 800 mM

Abs_{śr,standardu} = 1,235

Abs_{śr,substratu} = 1,577

RP	t [s]	średnia Abs	C0,rzecz,g [mM]	Cg [mM]	Cp [mM]	[ml/s]	 s]	α [%]	r [mM/s]
30	37	1,379	766,199	669,897	96,301	1,351	4,655	12,56871	20,68949
20	57	1,661	R=40x	807,181	-40,983	0,877	7,171	-5,34884	-5,71538
10	82	1,367		664,066	102,133	0,610	10,316	13,32981	9,90081
0	213	1,269			616,685	149,514	0,235	26,795	19,51374	5,57984

Cs = 1250 mM

Abs_{śr,standardu} = 1,010

Abs_{śr,substratu} = 1,665

RP	t [s]	średnia Abs	C0,rzecz,g [mM]	Cg [mM]	Cp [mM]	[ml/s]	 s]	α [%]	r [mM/s]
15	67,42	1,438	1235,9782	1067,469	168,509	0,742	8,481	13,63363	19,86795
7,5	117,05	1,520	R=50x	1128,340	107,638	0,427	14,725	8,70871	7,30992
0	169,5	1,637		1215,193	20,785	0,295	21,323	1,68168	0,97477
<0	235,59	1,446			1073,037	162,941	0,212	29,637	13,18318	5,49786

Cs = 1500 mM

Abs_{śr,standardu} = 0,891

Abs_{śr,substratu} = 1,812

RP	t [s]	średnia Abs	C0,rzecz,g [mM]	Cg [mM]	Cp [mM]	[ml/s]	 s]	α [%]	r [mM/s]
30	38,57	1,817	1524,8316	1529,040	-4,209	1,296	4,852	-0,27601	-0,86741
20	57,81	1,850	R=50x	1557,239	-32,407	0,865	7,272	-2,12531	-4,45616
10	97,39	1,867		1571,128	-46,296	0,513	12,252	-3,03616	-3,77878
0	218,35	1,859			1564,394	-39,562	0,229	27,468	-2,59453	-1,44028

Do dalszych obliczeń wzięto wyniki z tabel zaznaczone kolorem zielonym, tj. spełniające warunek

Cs [mM]	r [mM/s]
48,114	0,09679
94,263	0,30894
394,027*	0,13153*
1235,97823	0,975

* w celu nakreślenia wykresu M-M usunięto ten punkt

1. Wykres Michaelisa-Menten dla reakcji izomeryzacji glukozy do fruktozy.

Policzono odwrotności powyższych wartości w celu stworzenia wykresu Lineweavera-Burka:

1/Cs [1/mM]	1/r [s/mM]
0,020784	10,33166
0,010609	3,23687
0,002538	7,602544
0,000809	1,025878

2. Wykres Lineweavera-Burka dla reakcji izomeryzacji glukozy do fruktozy.

Korzystając z równania funkcji policzono parametry kinetyczne reakcji (K_M i V_max):

y = 467,35x + 0,1517

Stąd: V_max = 1 / 0,1517 = 6,592

K_M = 467,35 / 0,1517 = 3080,751

Reakcje izomeryzacji fruktozy do glukozy

Stężenie standardu C_st = 15 mM

Objętość próbki V_p = 50 ml

Objętość wolna reaktora V_r = 6,29 ml

Przykładowe obliczenia dla próbki nr 1

Cs = 50 mM

Abs_{śr,standardu} = 1,170

• Stężenie produktu dla RP = 15:

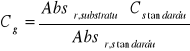
[mM]

[mM]

• Strumień przepływu V:
  
  

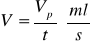
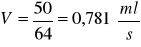
• Czas przebywania τ:
  
  

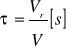
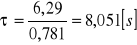
• Stopień przereagowania α:
  
  

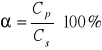
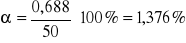
• Szybkość reakcji r:
  
  

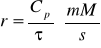
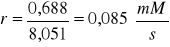
Wyniki zestawione zostały w tabelach:

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	r [mM/s]
15	64	0,054	0,688	0,781	8,051	1,37646	0,08548
7,5	94	0,110	1,415	0,532	11,825	2,82987	0,11965
0	148	0,176	2,257	0,338	18,618	4,51411	0,12123
<0	249	0,283	3,629	0,201	31,324	7,25848	0,11586

Cs = 100 mM

Abs_{śr,standardu} = 1,199

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	r [mM/s]
15	67	0,148	1,846	0,746	8,429	1,84606	0,21902
7,5	93	0,209	2,620	0,538	11,699	2,61994	0,22394
0	144	0,311	3,886	0,347	18,115	3,88611	0,21452
<0	358	0,539	6,740	0,140	45,036	6,73967	0,14965

Cs = 200 mM

Abs_{śr,standardu} = 1,204

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	r [mM/s]
15	82	0,244	3,040	0,610	10,316	1,51993	0,29469
7,5	112	0,402	5,012	0,446	14,090	2,50623	0,35576
0	147	0,521	6,495	0,340	18,493	3,24751	0,35122
<0	249	0,895	11,150	0,201	31,324	5,57517	0,35597

Cs = 400 mM

Abs_{śr,standardu} = 0,963

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	r [mM/s]
30	28,25	0,083	1,288	1,770	3,554	0,32208	0,36251
20	44,59	0,217	3,382	1,121	5,609	0,84545	0,60288
10	77,69	0,337	5,257	0,644	9,773	1,31429	0,53790
0	242,02	1,168	18,195	0,207	30,446	4,54870	0,59761

Cs = 600 mM

Abs_{śr,standardu} = 1,216

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	r [mM/s]
30	28,95	0,321	3,964	1,727	3,642	0,66064	1,08839
20	48,55	0,341	4,206	1,030	6,108	0,70107	0,68872
10	79,5	0,519	6,402	0,629	10,001	1,06702	0,64014
0	186,57	1,158	14,278	0,268	23,471	2,37973	0,60835

Cs = 800 mM

Abs_{śr,standardu} = 1,216

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	r [mM/s]
30	33,75	0,357	4,471	1,481	4,246	0,55889	1,05309
20	53,93	0,473	5,932	0,927	6,784	0,74153	0,87440
10	79,9	0,743	9,319	0,626	10,051	1,16482	0,92709
0	170,59	1,224	15,351	0,293	21,460	1,91890	0,71533

Cs = 1000 mM

Abs_{śr,standardu} = 0,953

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	R [mM/s]
80	45,86	0,177	2,780	1,090	5,769	0,27795	0,48179
60	68,51	0,403	6,346	0,730	8,619	0,63465	0,73637
40	102,48	0,712	11,213	0,488	12,892	1,12126	0,86973
20	252,86	1,467	23,097	0,198	31,810	2,30971	0,72610

Cs = 1250 mM

Abs_{śr,standardu} = 0,927

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	r [mM/s]
80	53,74	0,619	10,014	0,930	6,760	0,80115	1,48131
60	69,05	0,595	9,637	0,724	8,686	0,77094	1,10939
40	67,91	0,859	13,910	0,736	8,543	1,11281	1,62823
20	169,89	1,858	30,081	0,294	21,372	2,40647	1,40748

Cs = 1500 mM

Abs_{śr,standardu} = 0,937

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	r [mM/s]
80	55	0,955	15,293	0,909	6,919	1,01957	2,21036
60	69	0,764	12,231	0,725	8,680	0,81537	1,40901
40	111	1,043	16,697	0,450	13,964	1,11313	1,19573
20	274	2,058	32,940	0,182	34,469	2,19602	0,95564

Cs = 1750 mM

Abs_{śr,standardu} = 0,941

RP	t [s]	średnia Abs	Cp [mM]	[ml/s]	 [s]	α [%]	r [mM/s]
80	55,09	1,003	15,994	0,908	6,930	0,91394	2,30783
60	72,68	0,718	11,444	0,688	9,143	0,65394	1,25165
40	103,54	0,903	14,394	0,483	13,025	0,82252	1,10508
20	295,87	2,081	33,179	0,169	37,220	1,89592	0,89141

Do dalszych obliczeń wzięto wyniki z tabel zaznaczone kolorem zielonym, tj. spełniające warunek

Cs [mM]	r [mM/s]
50	0,11965
100	0,22394
200	0,35576
400*	0,53790*
600	0,60835
800	0,71533
1000*	0,72610*
1250*	1,40748*
1500	0,95564
1750*	0,89141*

* w celu nakreślenia wykresu M-M usunięto te punkty

3. Wykres Michaelisa-Menten dla reakcji izomeryzacji fruktozy do glukozy.

Policzono odwrotności powyższych wartości w celu stworzenia wykresu Lineweavera-Burka:

1/Cs [1/mM]	1/r [s/mM]
0,02	8,3574
0,01	4,4655
0,005	2,8109
0,0025*	1,8591*
0,001667	1,6438
0,00125	1,3980
0,001*	1,3772*
0,0008*	0,7105*
0,000667	1,0464
0,000571*	1,1218*

* w celu nakreślenia wykresu L-B usunięto te same punkty, co w poprzednim zestawieniu

4. Wykres Lineweavera-Burka dla reakcji izomeryzacji fruktozy do glukozy.

Korzystając z równania funkcji policzono parametry kinetyczne reakcji (K_M i V_max):

y = 370x + 0,9077

Stąd: V_max = 1 / 0,9077 = 1,102

K_M = 370 / 0,9077 = 407,624

Wyznaczenie stałej równowagi K_eq na podstawie stanu równowagi termodynamicznej:

Przyjęto założenie: A ~ C, zatem wartości absorbancji są w dobrym przybliżeniu równe wartościom odpowiednich stężeń. Wartości zaznaczone na czerwono nie były brane pod uwagę przy obliczaniu średnich (które posłużyły do dalszych obliczeń) :

Abs	Cg,0 (G) [mM]	Cg* (G+E) [mM]	CF* [mM]	Cg,0,śr [mM]	Cg*,śr [mM]	CF*,śr [mM]	Keq
1	1,909	1,102	0,807	1,920	1,069	0,859	0,803
2	1,67	1,085	0,585
3	1,931	1,021	0,910
1	1,866	1,055	0,811	1,841	1,090	0,752	0,690
2	1,872	1,085	0,787
3	1,786	1,129	0,657
1	1,663	1,048	0,615	1,750	1,025	0,725	0,708
2	1,793	1,011	0,782
3	1,793	1,015	0,778
1	0,693	0,376	0,317	0,678	0,362	0,316	0,874
2	0,671	0,364	0,307
3	0,669	0,345	0,324
1	2,029	1,032	0,997	2,005	1,088	0,917	0,843
2	2,019	1,116	0,903
3	1,967	1,116	0,851
1	1,464	0,778	0,686	1,473	0,785	0,688	0,877
2	1,483	0,792	0,691
3	1,473	0,785	0,688

Przykładowe obliczenia:

• Stężenie C_F*:
  
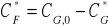
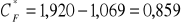
  [mM]

• Stała równowagi K_eq (ze stężeń równowagowych):

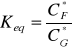
• Średnia stała równowagi K_eq,śr (średnia arytmetyczna):

Obliczono również stałą równowagi K_eq z równania Haldana, używając wyliczonych wcześniej wartości parametrów kinetycznych:

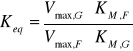
gdzie indeksy G/F oznaczają odpowiednio wyliczone wartości dla glukozy i fruktozy.

0,791

Wnioski

Przy tworzeniu wykresów Michaelisa-Menten oraz Lineweavera-Burka, odpowiednio dla glukozy i fruktozy, pod uwagę brane były te punkty szybkości reakcji, dla których stopień przereagowania α był mniejszy lub równy 3% (początkowe warunki reakcji). W przypadku wykresu dla glukozy, wiele wartości było ujemnych, bądź też stopień przereagowania był zbyt duży, w związku z czym należało znaczną część punktów odrzucić, co z kolei wpłynęło negatywnie na dokładność wykresów. Co ciekawe, wykres dla fruktozy nie sprawił aż takich problemów i wartości na nim wydają się być wiarygodne.

Ze wspomnianych wykresów wyliczono tzw. pozorne parametry kinetyczne reakcji: V_max i K_M, porównując je następnie ze sobą. Wartości prezentują się następująco:

GLUKOZA		FRUKTOZA
Vmax	6,592	Vmax	1,102
Km	3080,751	Km	407,624

Stałą równowagi K_eq wyznaczono korzystając z dwóch metod: doświadczalnie oraz ze stałej równowagi termodynamicznej. Wyliczone wartości są do siebie bardzo zbliżone, różnią się o wartość ΔKeq = 0,799 - 0,791 = 0,008, a więc bardzo niewiele - pozwala to stwierdzić poprawność wykonanych obliczeń.

Rozbieżności można tłumaczyć różną dostępnością dla substratu enzymu, który jest immobilizowany na złożu w porównaniu do enzymu natywnego, który jest „wolny”. Wpływ na wyniki może mieć też temperatura, w której przeprowadzono proces (tj. 40 st.C), podczas gdy optimum temperaturowe dla izomerazy to ok.65 st.C (dane literaturowe).

Sprawozdanie 3. Strona 10 z 13	Politechnika Wrocławska Wydział Chemiczny	Dr hab. Jolanta Bryjak, prof. PWr Pon, godz. 13:15, bud.C6/123A
Laboratorium Inżynieria Bioreaktorów	Wyznaczanie stałych równania kinetycznego reakcji izomeryzacji D-glukozy do D-fruktozy	Wojciech Ślęczek 168560 Maciej Duda 168516

---