W okręgu o promieniu 4cm narysowano dwa promienie pod kątem 30o. Oblicz długość dwóch łuków, na które okrąg został podzielony.
W okręgu poprowadzono cięciwę o długości 6cm odległa o 3cm od środka okręgu. Oblicz długość łuków okręgu, na które dzieli ten okrąg cięciwa.
W kole o promieniu 6cm narysowano dwa promienie pod kątem 45o. Oblicz pola dwóch wycinków, na które koło zostało podzielone.
W kole o promieniu 4cm poprowadzono cięciwę o długości 4cm. Oblicz pole powstałego odcinka koła.
Znajdź kąty
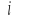
Oblicz kąty trójkąta ABC
Znajdź kąty
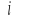
Kąt środkowy i wpisany są oparte na tym samym łuku. Suma ich miar jest równa 150o. Jaka jest miara kąta wpisanego i środkowego?
Ostrokątny trójkąt równoramienny ABC o podstawie AB wpisany jest w okrąg o środku S. Kąt ASB ma miarę 100o. Oblicz miary kątów tego trójkąta.
Ostrokątny trójkąt równoramienny ABC o podstawie AB jest wpisany w okrąg o środku S, przy czym kąt SAB ma miarę 40o. Oblicz miarę kąta CAB.
Przez punkt A poprowadzono styczną do okręgu o promieniu 3 cm. Odległość punktu A od środka okręgu wynosi 5 cm. Znajdź odległość punktu A od punktu styczności.
Okrąg o promieniu 4 cm jest styczny zewnętrznie do okręgów o promieniu 2 cm. Poprowadzono prostą styczną do tych okręgów. Prosta ta nie przechodzi przez punkt styczności okręgów. Oblicz odległości między punktami styczności.
Oblicz obwód i pole sześciokąta foremnego, którego bok ma długość 2 cm.
Oblicz długość promienia okręgu wpisanego i opisanego na sześciokącie foremnym, którego bok ma długość 8 cm.
Oblicz stosunek pola koła wpisanego w sześciokąt foremny do pola koła opisanego na tym samym sześciokącie foremnym.Z dwunastokąta foremnego odcięto trzy wycinki kół, których środkami są pewne wierzchołki dwunastokąta, a ich promienie mają długość równą długości boku dwunastokąta. Wiedząc, że suma pól tych wycinków jest równa 80 π cm2, oblicz długość boku dwunastokąta.
Pole koła wpisanego w sześciokąt foremny wynosi 2 9cm. Oblicz pole koła opisanego na tym sześciokącie.
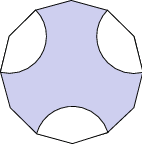
Oblicz pole zacieniowanej figury:
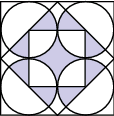
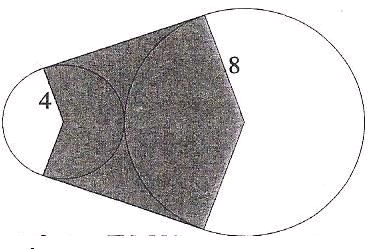
10
10
Wyszukiwarka