Rozwiązania zdań
Wektory. Iloczyn skalarny.
1. Dane są punkty ![]()
(a) Znaleźć wektory ![]()
, ![]()
, ![]()
, ![]()
, gdzie ![]()
- środek odcinka ![]()
.
a = [-2-(-2); -1-3] = [0;-4], b = [6;0], c = [6;-4], M((-2+(-2))/2; (3+(-1))/2) = (-2;1),
d = [0;2].
W przypadku, gdy punkty ![]()
są punktami płaszczyzny Oxy to ich współrzędne w przestrzeni R3 są odpowiednio równe ![]()
Wtedy
a = [0;-4;0], b = [6;0;0], c = [6;-4;0], M((-2+(-2))/2; (3+(-1))/2;(0+0)/2) = (-2;1;0),
d = [0;2;0].
(b) Obliczyć długości wektorów ![]()
,![]()
.
![]()
(c) Obliczyć iloczyny skalarne ![]()
![]()
(d) Znaleźć wektor ![]()
, ![]()
,![]()
,
![]()
(e) Znaleźć wektor jednostkowy (wersor) równoległy do ![]()
![]()
Znaleźć kąty ![]()
pomiędzy wektorami, odpowiednio, ![]()
.
![]()
, ![]()
, ![]()
Znaleźć ![]()
.
![]()
, ![]()
, ![]()
Znaleźć wektor ![]()
taki, że ![]()
.
![]()
Znaleźć punkt ![]()
taki, że ![]()
=![]()
Nieznane współrzędne punktu D oznaczmy przez (x,y). Wtedy wektor ![]()
=[x-(-2);y-1].
Warunek ![]()
=![]()
przekształca się w równość wektorów
[x-(-2);y-1] = ![]()
=![]()
= [0-18;-8].
Ta równość wektorowa jest równoważna równości odpowiednich współrzędnych
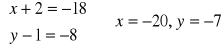
Punkt D ma współrzędne (-20;-7).
2. Oblicz współrzędne wierzchołków CD równoległoboku ABCD, jeżeli A=(2,3), B=(5,-1) a przekątne przecinają się w punkcie M=(4,1).
A
Z rysunku wynikają podstawowe związki wektorowe:
= 2
,
= 2
,
Gdy nieznane współrzędne punktu C oznaczmy przez (x,y), związek
= 2
przyjmie formę
[x-2;y-3]= 2*[4-2;1-3] = [4;-4] .
Stąd x=6, y=-1
Gdy nieznane współrzędne punktu punku D oznaczmy przez (u,v), związek
= 2
przyjmie formę
[u-5;v-(-1)] = 2*[4-5;1-(-1)] = [-2;4].
Stąd u=3, v=3
3. Dla jakich liczb m, k wektory [2,-5] i [2m-3, 3k+4] są przeciwne.
Przeciwieństwo wektorów [2,-5] , [2m-3, 3k+4] oznacza że
-[2,-5] = [2m-3, 3k+4] .
Porównując współrzędne 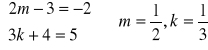
4. Udowodnij równość ![]()
i podaj jej interpretację geometryczną.
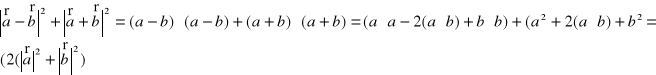
Z twierdzenia cosinusów dla trójkąta ABC wynika, że
![]()
Oznacza to, że
![]()
Z twierdzenia cosinusów dla trójkąta ABD wynika, że
![]()
Oznacza to, że
![]()
Ponieważ kątB = π- kątA , więc ![]()
.
![]()
=![]()
+ ![]()
=![]()
+ ![]()
= ![]()
5. Mamy dane : ![]()
Wiedząc, że kąt między tymi wektorami wynosi ![]()
, oblicz , korzystając z tw. cosinusów długość sumy tych wektorów.
![]()
= 9+25-3*5*1/2 = 26,5 ![]()
6. Dla jakiej liczby a wektory [2a+3, a-2] , [ a-4, 3a] są prostopadłe ?
Korzystamy z twierdzenia
(a![]()
[2a+3, a-2] ۰[ a-4, 3a] = (2a+3 )* (a-4 )+(a-2)*(3a) = (2a2-5a-12)+(3a2-6a) = 5a2-11a-12 = 0
Rozwiązując równanie
5a2-11a-12 = 0 ![]()
, a1=(11-19)/10 = -0,8 , a2= 3
7. Dane są punkty A=(2,4) i B=(-3,2). Znaleźć punkt X , który dzieli odcinek AB w stosunku ![]()
.
Nieznane współrzędne punktu X oznaczmy przez (x,y). Wtedy wektor ![]()
.
Ponieważ punkt X , który dzieli odcinek AB w stosunku ![]()
. Oznacza to, że ![]()
.
Stąd
0,4*[-5;-2] = [x-2;y-4] 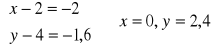
Dane są punkty ![]()
(a) Znaleźć wektory ![]()
, ![]()
, ![]()
, ![]()
, gdzie ![]()
- środek odcinka ![]()
.
a = [-2-(-1);-1-(-2);4-3] = [-1;1;1] , b = [6;0;-3] , c = [5;1;-2]
M ((-1+(-2))/2;(-2+(-1))/2;(3+4)/2) = (-(3/2);-(3/2);7/2),
d= [-1/2;1/2;1/2]
(b) Obliczyć długości wektorów ![]()
![]()
, ![]()
, ![]()
(c) Obliczyć iloczyny skalarne ![]()
, ![]()
.
![]()
, b۰c = 36, a۰c = =6, a۰d = 1/2,
(d) Znaleźć wektor ![]()
, ![]()
.
![]()
= 2[-1;1;1] +(-3) [6;0;-3] + [5;1;-2] = [-2;2;2] + [-18;0;9] + [5;1;-2] = [-15;3;-9]
![]()
= [3/2-2-20;-3/2+2-4;-3/2+2+8] = [-201/2;1-41/2;81/2]
![]()
(e) Znaleźć wektor jednostkowy (wersor) równoległy do ![]()
wb= = [![]()
]
(f) Znaleźć kąty ![]()
pomiędzy wektorami, odpowiednio, ![]()
cos α = ![]()
= ![]()
, cos β = ![]()
, cos γ = ![]()
,
(g) Znaleźć ![]()
![]()
, ![]()
, ![]()
(h) Znaleźć wektor ![]()
taki, że ![]()
.
Od strony formalnej wektor ![]()
nie istnieje, gdyż nie można wykonywać działań na wektorach w różnych przestrzeniach. (na różnej ilości współrzędnych wektorów).
Z drugiej strony wektor [3;-2] często oznacza wektor leżący w płaszczyźnie Oxy podprzestrzeni R3. Wtedy jego jego trzecia współrzędna w R3 jest równa 0.
Wówczas równanie ![]()
ma postać ![]()
i usunięte zostały formalne przeszkody w rozwiązaniu tego równania wektorowego.
-4x = [3:-2;0]-3a-2d ↔ x = (-1/4)( [3:-2;0]-3a-2d ) = [![]()
] =
[-7/4;3/2;1]
(i) Znaleźć punkt ![]()
taki, że ![]()
=![]()
.
Nieznane współrzędne punktu D oznaczmy przez (x,y,z). Wtedy wektor ![]()
.
![]()
=![]()
= 2a-3b = [-20;2;11}
Porównując współrzędne 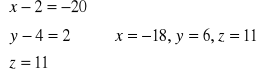
2. Dany jest wektor ![]()
. Obliczyć ![]()
.![]()
=![]()
=
![]()
3* = 3*![]()
3. Dane są wektory ![]()
, ![]()
![]()
. Obliczyć ![]()
.
![]()
= ![]()
= ![]()
4. Dla jakich liczb m, k wektory [2,-5,-7] i [2m-2, 3k-2,-3m+k ] są przeciwne.
Przeciwieństwo wektorów [2,-5,-7] , [2m-3, 3k+4,-3m+k] oznacza że
-[2,-5,-7] = [2m-3, 3k+4,-3m+k].
Porównując współrzędne 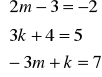
otrzymujemy sprzeczny układ równań.
Nie istnieją takie liczby m, k by wektory [2,-5,-7] i [2m-2, 3k-2,-3m+k ] były przeciwne
5. |a| = 4 , |b| = 4 , < a,b = π/3. Oblicz:
a) |4a-3b|
|4a-3b|2 = (4a-3b)۰ (4a-3b) = 16(a۰a) - 12(a۰b) - 12(b۰a) +9(b۰b) = 16|a|2 -24|a||b|cos< a,b +9|b|2 = 16*16 - 24*4*4*1/2+ 9*16 = 16*(16 -12+9)= 208 → |4a-3b| = ![]()
b) (2a+3b)۰(-4a+5b)
(2a+3b)۰(-4a+5b) = -8(a۰a)-2(a۰b)+15(b۰b) = -8*16-2*4*4*1/2+15*16 = 16*6 = 96
6. Dla jakiego m wektory [m+1;m-1;2], [3;2m;-5] są prostopadłe?
Prostopadłość wektorów [m+1;m-1;2], [3;2m;-5] jest równoważna temu, że
([m+1;m-1;2]۰ [3;2m;-5]) = 0 = 3*(m+1)+ m*(m-1) -10 = m2+ 2m+3 = 0.
Równanie m2+ 2m+3 = 0 nie ma rozwiązań, gdyż jego ∆= 4-12<0
7. Dane są punkty A(2-m;3;m+1), B(2;m-1;4), C(2;m;-1). Dla jakiego m wektory
![]()
są prostopadłe?
Prostopadłość wektorów ![]()
jest równoważna temu, że ![]()
.
![]()
= [ 2-(2-m);m-1-3;4-(m+1)] = [m;m-4;-m+3], ![]()
= [m;m-3;-m-2].![]()
≡ [m;m-4;-m+3]۰ [m;m-3;-m-2] = m2+(m-4)*(m-3)+(-m+3)*(-m-2) =
3m2-7m-m-6 = 3m2-8m-6 = 0
∆= 64+72 = 136 stąd ![]()
, ![]()
.
8. |a| = 2 , |b| = 4 , < a,b = π/4. Dla jakiego t wektory 3a-tb , a są prostopadłe?
Prostopadłość wektorów 3a-tb , a jest równoważna temu, że (3a-tb)۰a = 0 .
0 = (3a-tb)۰a = 3a۰a- ta۰b = 3|a|2- t*|a|*|b|*cos< a,b = 12 -4t*![]()
. Stąd
![]()
.
9. Dla jakich m wektory [m+2;m-1;3], [4m;m;3m] sa równoległe?
Równoległość wektorów [m+2;m-1;3], [4m;m;3m] jest równoważna temu, że
[m+2;m-1;3] = t[4m;m;3m] = [4tm;tm;3tm].
Porównując współrzędne 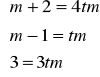
otrzymujemy tm = 1, m=2 .
C
D
M
B
D
C
a+b
a
a-b
B
A
b
A3
b
c
d
a
A1
M
A2
Wyszukiwarka