1.4.5 Prawo przenoszenia się błędów
Związek wykazujący sposób gromadzenia się błędów średnich niezależnych spostrzeżeń bezpośrednich, występujących w danej funkcji, nosi nazwę prawa przenoszenia się błędów (propagacja błędów). Jest to jedno z podstawowych praw rachunku wyrównawczego, stosowane przy wszelkich analizach dokłądnościowych zarówno a priori, jak i a posteriori - dla dla spostrzeżeń nie biorących udziału w wyrównaniu jak i spostrzeżeń skorelowanych wspólnym wyrównaniem. Zastosowanie prawa przenoszenia sie błędów sprowadza sie w zasadzie do określenia błędów średnich funkcji spostrzeżeń i może być stosowane tylko do funkcji będących liniowymi bądź sprowadzonych do postaci liniowej. Będziemy rozważać tylko poszczególne rodzaje funkcji wiążących spostrzeżenia bezpośrednie nie uzależnione wyrównaniem (nie skorelowane).
Do podania końcowych wzorów dla szczególnych postaci funkcji wykorzystano twierdzenie o wariancji, nadając im interpretację i oznaczenia według zasad rachunku wyrównawczego.
A.Określenie błędu średniego wielokrotności spostrzeżenia
Przypuścmy, żę rozpatrujemy funkcję daną równaniem
F = a X
gdzie a jest stałą (wielokrotnością zmiennej niezależnej X). Zadaniem jest określenie błędu średniego ![]()
tej funkcji. Wyobrażmy sobie bowiem, że w wyniku określenia wielkości X, dokonaliśmy n obserwacji otrzymując poszczególne wartości spostrzeżeń L oraz .Możemy zatem obliczyć błąd średni wielkości X wzorem
![]()
Ponieważ błędy wielkości a X są z uwagi na stałość liczby a wielkości a-krotnie większymi od błędów wielkości X, mamy tu do czynienia z błędami a i. Wykorzystując twierdzenie o wariancji iloczynu stałej przez zmienną losową otrzymamy zapis
V(F) = V(aX) = a2V(X),
którego odpowiednikiem w rachunku wyrównawczym są wzory
![]()
(1.76)
Błąd średni iloczynu stałej przez wielkość o danym błędzie równa się iloczynowi stałej przez ten błąd, czyli
![]()
(1.77)
B. Błąd średni sumy (różnicy) spostrzeżeń
Jest określona funkcja
F = X + Y
przez dwa szeregi spostrzezeń: ![]()
(dla i = 1,2, ... , n) wielkości X, ![]()
` (dla i = 1,2, ... , n) wielkości Y.
Niech zmienną losową X będa wartości błędu , zaś zmienna losową Y będą wartości błędu .
Zgodnie z twierdzeniem o wariancji sumy niezależnych zmiennych losowych będzie
![]()
Wyrażając wariancję zmiennych losowych przez błędy średnie, otrzymamy
![]()
(1.78)
Powyższy wzór rozciąga się również na dowolną ilość składników tak dla sumy, jak i dla różnicy.
W przypadku gdy błedy średnie poszczególnych wielkości są sobie równe, to znaczy, mx = my = ..... m0 , wówczas prawo przenoszenia się błędów przybiera dla n składników szczególną formę
![]()
(1.79)
Oznacza to, że błąd sumy n spostrzeżeń, z których każde jest obarczone błędem średnim m0, rośnie proporcjonalnie do pierwiastka z ilości składników. Z wzoru (1.79) korzystamy często dla obliczenia wagi sumy spostrzeżeń, a mianowicie dla obliczenia wagi funkcji F równej pF
![]()
(1.80)
C. Błąd średni funkcji liniowej
Niech będą określone z pomiarów bezpośrednich wielkości X, Y, Z o znanych błędach średnich mx, my, mZ. Na ich podstawie wyznaczamy niewiadomą daną równaniem
F = aX + bY + cZ
gdzie: a, b, c są znanymi dowolnymi współczynnikami. Poszukujemy błędu średniego tej funkcji. Przyjmując, że aX, bY i cZ są wielokrotnościami funkcji, więc na mocy (1.76) ostatecznie otrzymamy
![]()
(1.81)
D. Błąd funkcji o dowolnej postaci
Najogólniejszy przypadek powyższych rozważań zajdzie,kiedy funkcję F = F(X, Y, Z) mamy wyznaczyć na podstawie bezpośrednio pomierzonych wielkości X, Y, Z o znanych błędach średnich mx, my, mZ. Zakłada się, że funkcja
F = f(X, Y, Z,...)
jest rozwijalna w szereg Taylora w okolicy punktu, który reprezentuje przybliżenie szukanych wartości, a wyrazy wyższych potęg nadwyżek nad wartościami przybliżonymi są dla danych celów bez znaczenia. Nadwyżki te, jako bardzo małe zmiany argumentów spostrzeżeń, odpowiadają wartościom błędów. Jeżeli podaną funkcję zamienimy na postać liniową, to otrzyma się funkcję
![]()
z której, po przeniesieniu wyrazu wolnego na lewą stronę, otrzymamy różniczkę zupełną
dF = ![]()
![]()
Stosując wzór na błąd średni funkcji liniowej ostatecznie napiszemy
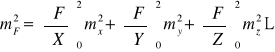
,
gdzie różniczki nieskończenie małę zastąpiono błędami o skończonych wartościach (np. dx = X-X0 = x = mx itp.).
Oznaczając pochodne cząstkowe
![]()
dojdziemy do wzoru
![]()
(1.82)
Wzór (1.82) można wyprowadzić bezpośrednio z twierdzenia o wariancji. Dla rozpatrywanej funkcji F należy uwzględnić, że wariancja stałej c = ![]()
równa się zeru oraz, że wariancja iloczynu stałej przez zmienną losową jest równa kwadratowi stałej razy wariancja zmiennej losowej.
![]()
![]()
![]()
Wyszukiwarka