Maksymilian Rudnik Gdańsk, dn.21.11.2009

Zaoczne studia inżynierskie

Semestr 1 grupa laboratoryjna 2/4

Ćwiczenie nr 2

Pomiary oscyloskopowe

WYDZIAŁ ELEKTRONKI TELEKOMUNIKACJI I INFORMATYKI KATEDRA METROLOGII I SYSTEMÓW ELEKTRONICZNYCH LABORATORIUM METROLOGII I TECHNIKI EKSPERYMENTU GRUPA ..2/4.....
Ćwiczenie nr 2 Pomiary oscyloskopowe	Imię i nazwisko	Maksymilian Rudnik
		Data wykonania ćwiczenia	21.11.2009 r.
		Data odbioru sprawozdania
		Ocena zaliczenia
		Uwagi i podpis

Cel ćwiczenia

Celem tego ćwiczenia było zapoznanie się z oscyloskopem oraz jego praktycznymi zastosowaniami. W trakcie tego ćwiczenia wykonywane było wzorcowanie kanału X i Y, pomiary napięcia i czasu, pomiary napięć różnicowych, pomiary parametrów impulsów, obserwacje przebiegów układów w układach cyfrowych oraz obserwacje charakterystyk I/U diod półprzewodnikowych.

Zadania pomiarowe

1. Wzorcowanie kanału Y oscyloskopu napięciem stałym.

Za pomocą tego doświadczenia możliwe jest wyznaczenie stałej napięciowej kanału Y. Obliczymy to metodą najmniejszych kwadratów, zaś potrzebne dane uzyskamy w wyniku odchylania napięciem stałym plamki od położenia zerowego, o określoną liczbę działek. Uzyskane wyniki zawarte w tabelce oraz wyliczenia metodą najmniejszych kwadratów są prezentowane poniżej. Wzorcowanie kanału Y przeprowadziłem dla stałej napięciowej równej D_y = 1V/cm.

Wyniki wzorcowania kanału Y

y	cm	1	2	3	4	-4	-3	-2	-1
Uy	V	1,005	2,003	2,935	3,950	-3,898	-2,916	-1,922	-0,978
Dypom	V/cm	1,005	1,0015	0,9783	0,9745	0,9745	0,972	0,961	0,978
δD	%	0,062	0,058	0,033	0,044	0,029	0,027	0,016	0,033
Dyobl	V/cm	0,9463

Aby wypełnić całkowicie tabelę należy obliczyć wpierw D_yobl a potem δ_D .

• Jako D_yobl przyjmujemy współczynniki kierunkowe takich prostych U_y = m_yy + n_y i, dla których sumy S_y kwadratów odchyłek poszczególnych punktów /yi,Uyi/ od prostych osiągają minimum. Aby wyznaczyć współczynnik kierunkowy prostej:

• U_y = m_yy + n_y

• dla kanału Y poszukuje się minimum sumy

to jest
, skąd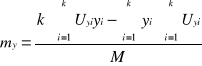

oraz
, skąd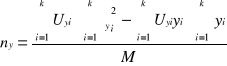

gdzie

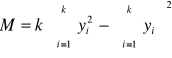
W tym miejscu warto zauważyć, że przedział y_i jest symetryczny:

y_i = { 1, 2 ,3 , 4, (-4), (-3), (-2), (-1)}

wyrażenie

a w związku z tym odpowiednie wzory na M, m_y i n_y znacząco się nam upraszczają :

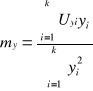
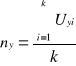
Ilość pomiarów czyli k = 8; z kolei wartość wyrażeń

(1,005) + (2,003) +(2,935) + (3,950) + (-3,898) + (-2,916) + (-1,922) + (-0,978) = 0,179

60

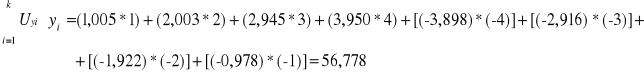
W oparciu o te wyliczone wartości można policzyć już m_y i n_{y :}

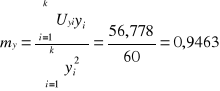
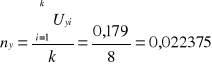
Otrzymujemy w ten sposób równanie postaci:

U_y = m_yy + n_y = 0,9463 y + 0,02375

gdzie m_y = D_yobl = 0,9463

Następnie wyliczamy błąd względny według wzoru :

δ_D = (D_ypom - D_yobl) / D_yobl

i wypełniamy po kolei tabelę brakującymi wartościami.

Wykres przedstawia zależność błędu względnego δ_D w funkcji napięcia U_y

Z wykresu wynika, że największe błędy wystąpiły na początku pomiaru. Zacząłem bowiem od pomiaru dodatnich napięć: 1V, potem 2 V itd. , a następnie zgodnie z tabelą zacząłem pomiary dla napięć ujemnych od wartości (- 4V) do (-1V). Jak widać wyraźnie na wykresie w miarę jak dokonywałem dalszych pomiarów, wzrastała moja precyzja kalibracji. Spowodowane to było min. moim brakiem „obycia” z oscyloskopem jako urządzeniem pomiarowym, a także z dalszymi czynnościami, które potem wykonałem.

Przede wszystkim dokładniej ustawiłem ostrość oraz zmniejszyłem jasność plamki do niezbędnego minimum. Zmniejszając wielkość plamki spowodowałem ustalenie dokładniejszego wyniku niż na początku pomiarów (zmniejszenie błędu względnego z 1, 643 % do 0.09 %) . Podejrzewam, że w miarę mojego „oswajania się” z przyrządem byłbym w stanie ustalić jeszcze lepsze pomiary - cóż, potwierdza się stare porzekadło, że „praktyka czyni mistrza”. Zatem w moim przypadku o wyniku pomiaru decydująca rolę odegrała precyzja ustawienia parametrów początkowych plamki, oraz w konsekwencji idąca za tym precyzja w dokonywaniu bezpośredniego odczytu z ekranu oscyloskopu.

2. Pomiary napięcia i czasu oscyloskopem

W ćwiczeniu tym należy wyznaczyć stałą czasową układu całkującego na podstawie pomierzonych przy pomocy oscyloskopu wartości napięcia i czasu. Następnie należy wyliczyć stałą czasową na podstawie znanych wartości elementów RC, a następnie porównać oba wyniki.

W badanym układzie pomiarowym wartość rezystora R wynosiła odpowiednio 995 Ω, zaś kondensatora C = 103 nF. Wyniki pomiarów oraz wartości wyliczone są pogrupowane w poniższej tabeli :

U(t1)	V	3,64
U(t2)	V	0,38
t	s	280
RCteor	s	102,485
RCpom	s	123,92
δRC	%	20,92

Ogólną zależność dla tego obwodu całkującego można wyrazić za pomocą wzoru:

Po przekształceniu wzoru otrzymujemy:

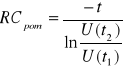
Wzór na wartość stałej czasowej w oparciu o znane wartości elementów RC :

RC_teor = R*C

Wzór na wartość błędu względnego δ_RC :

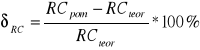
Jak wynika z tabeli, wartości stałej czasowej układu całkującego wyliczone i pomierzone są ze sobą prawie identyczne (różnica wynosi niecałe 1,7 s), zaś błąd względny nie przekracza 1,7 %.

3. Obserwacja przebiegów w układach cyfrowych

Celem tego ćwiczenia była obserwacja przebiegów cyfrowych w układzie wykorzystującym licznik binarny 7493 oraz bramkę AND typu 7408. Z przeprowadzonych pomiarów wynika, że na kolejnych wyjściach licznika 7493, oznaczonych A, B, C, D, zaobserwowane przebiegi różniły się od siebie czasem trwania jednego okresu. Dla każdego z wyjść zbadano ilość przypadających na jeden okres okresów przebiegu podstawowego T _in.

T_A = 2 x T _in

T_B = 4 x T _in

T_C = 8 x T _in

T_D = 16 x T _in

Nasuwa się dość oczywisty wniosek, że w tej konfiguracji licznik binarny 7493 pracuje w trybie dzielnika częstotliwości przez 2 - tj. na każdym z kolejnych wyjść badana częstotliwość jest dwa razy mniejsza od częstotliwości wyjścia poprzedniego.

Dla wygenerowanego przebiegu cyfrowego zanotowałem następujące wartości napięć:

U_HI = 3,36 V

U_LO = 116 mV

Kolejnym zadaniem w ramach tego ćwiczenia była obserwacja przebiegów wejściowych i wyjściowych na bramce typy AND. Wyjście bramki oznaczone jako OUT podłączyłem do wejścia oscyloskopu oznaczonego CH1, zaś za pomocą wejścia CH2 badałem przebiegi wejściowe na bramce. W punkcie IN2 obserwowany przebieg na CH2 był niczym innym jak sygnałem podstawowym, doprowadzonym bezpośrednio z generatora. Z kolei w punkcie IN1 obserwowany przebieg miał już inne parametry - ponieważ pochodził z wyjścia D licznika binarnego, zatem jego okres był szesnaście razy większy od okresu podstawowego. Przebieg zaobserwowany na ekranie oscyloskopu, a pochodzący z wyjścia OUT bramki, prezentował się dość ciekawie - na ekranie widoczne były „paczki” impulsów przedzielone linia ciągłą w okolicy zera. Okres impulsów wewnątrz paczki równał się okresowi przebiegu wejściowego T _in , zaś czas jej trwania równał się połowie czasu trwania okresu T_D Wytłumaczenie jest proste - dla bramki AND w momencie, gdy na jednym z wejść panuje niski stan, stan wyjścia przyjmuje również poziom niski. Dopiero podanie na oba wejścia stanu wysokiego powoduje, że wyjście przyjmuje stan wysoki (patrz Tabela prawdy dla bramki AND). W naszym przypadku można powiedzieć, że niejako sygnałem sterującym bramki był sygnał wyjściowy T_D licznika binarnego.

Tabela prawdy dla bramki AND

IN1	IN2	OUT
0	0	0
0	1	0
1	0	0
1	1	1

4. Automatyczne pomiary parametrów impulsów w przebiegu okresowym

Celem ćwiczenia jest pomiar odpowiednich wartości w przebiegu okresowym za pomocą wbudowanej w oscyloskop dodatkowej aparatury pomiarowej. Za pomocą takiego trybu można w dość szybki, a także dokładny sposób otrzymać szukane parametry sygnału bez żmudnych obliczeń - przyspiesza i usprawnia to znacznie prace z przyrządem.

Po wygenerowaniu sygnału w generatorze i podaniu go na wejście oscyloskopu otrzymałem następujące wartości sygnału ujęte w tabeli:

Vpp	V	4,16
Vrms	V	2,8
Vavg	V	1,12
f (F)	Hz	930,2
T	μs	945,0
tw (W+)	μs	237
k (DC+)	%	25,08

5. Obserwacja charakterystyk diod półprzewodnikowych I = f (U) w obszarze przewodzenia

Celem ćwiczenia jest obserwacja charakterystyk diod półprzewodnikowych: germanowej, krzemowej i LED w zakresie przewodzenia. Po prawidłowym zestawieniu układu pomiarowego otrzymałem na ekranie oscyloskopu wykres zależności prądowo - napięciowej dla danego typu diody. Następnie z wykresu (dla każdej z diod) odczytałem wartość napięcia przewodzenia U_f dla prądu I = 25 mA. Wyniki zanotowałem w tabelce. Na podstawie otrzymanych wartości napięcia obliczyłem i wstawiłem do tabeli wartości rezystancji statycznych z ogólnego wzoru:

Na wykresach charakterystyk prądowo - napięciowych diod w punkcie I=25 mA narysowałem styczną do wykresu, a następnie zaznaczyłem przedział ΔI dla którego odczytałem odpowiadające mu wartości napięcia przewodzenia. Obydwa uzyskane w ten sposób zestawy liczb wpisałem do tabeli. Pozostało tylko wyliczenie rezystancji dynamicznej poszczególnych diod. Wzór na tą rezystancję przedstawia się następująco:

Typ diody	Uf [V]	R [Ω]	ΔU [V]	ΔI [mA]	rd [Ω]
germanowa
krzemowa
LED

Oczywiście wyliczone w ten sposób wartości rezystancji odbiegają nieco od rzeczywistych - głównie ze względu na niedokładności w przerysowywaniu wykresu zależności z ekranu oscyloskopu. Dokładniejsza, lecz bardziej żmudna i czasochłonna jest metoda analizy charakterystyki diody „punkt po punkcie”, przy pomocy woltomierza, amperomierza i zasilacza stabilizowanego. Jednakże pomiar oscyloskopowy daje już nam na wstępie możliwości zgrubnego określenia charakterystycznych wartości dla danego półprzewodnika, a przy tym jest to metoda szybsza w stosunku do poprzednio wymienionej.

Strona 8 z 8

---