Elektro-drgania  klasy 3 ogólne

Forma testowa - 1200 [s] - grupa A)

1. Wykres przedstawia 3 postacie funkcji sin(x) dla różnych postaci zmiennej x . Na podstawie jego analizy przerobić (tzn. narysować) go w wykres wychyleń w 3-ch układach drgających dla których spełnione są następujące warunki:

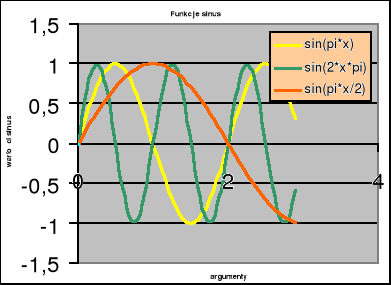
2. To 2 typowe układy drgań.

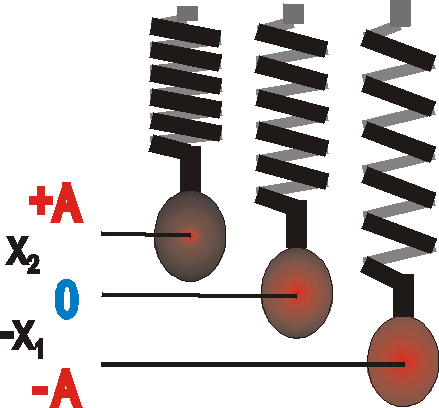
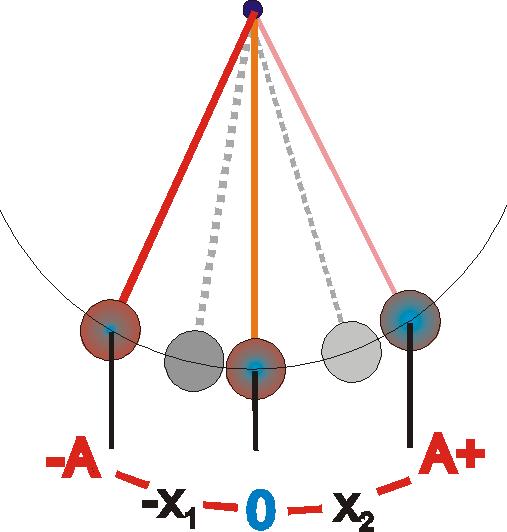
Forma zadaniowa - 1200 [s] - grupa B)

Do wyboru jeden z problemów:

Zad 1.

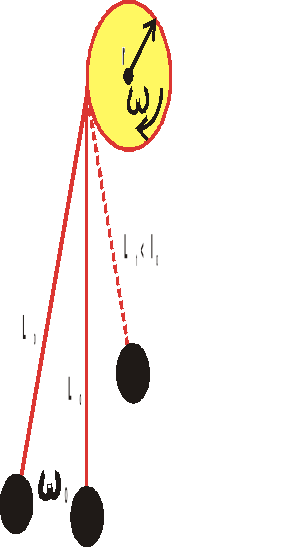
Potrzebne zależności:

;

;
;
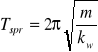
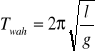
; π = 3

x(t) = A sin ( ω t ± ϕ ); x_max = A;

v(t)= ωA cos ( ω t ± ϕ ); v_max = ω A ;

a(t) = - ω²A sin ( ω t ± ϕ ); a_max = ω² A;

Zad 2.

Trzy oscylatory (od lewej k₁ = 0,6 [N/m] , m₁ = i [kg] , k₂ = 0,4 [N/m] , m₂ = j [kg] , k₃ = 0,2 [N/m],m₃ = 0,2 [kg] ) i A₁ = A₂ = A₃ = A₄ =1 [cm]. Masa m₁ jest tej samej gęstości co m₃ , zaś m₂ stanowi średnią arytmetyczną mas m₁ i m₃ . Obliczyć i wyznaczyć proporcję okresów i energii całkowitych tych oscylatorów zapisując wynik w postaci: a) T₁ : T₂ : T₃ = k : l : m ; b) E₁ : E₂ : E₃ = n : o : p .

Zad 3.

Resor samochodowy pod ciężarem masy 400 kg (na 1 koło) ulega ugięciu o 40 cm.

1. Jaki jest okres drgań resoru?

2. Jak zmieni się po obciążeniu 6 osób po 70 kg każda?

3. Samochód z w/w resorem porusza się z prędkością 72 km/h po „kocich łbach”. Przy jakiej ich średniej odległości będzie groźny rezonans drgań.

4. W jak głęboki dołek może „wpaść” samochód aby energia drgań wytrzymała ten spadek.

I to by było na tyle.

1. T₁ < T₂ < T₃ i oś pozioma to skala czasu rzeczywistego w 10^-2 [s].

2. A₁ = ½ A₃ = ¼ A₂ i oś pionowa to skala odległości w [mm].

3. Wyznacz prędkości max. w tych drganiach.

4. Jak długo od startu wszystkie trzy wychylenia były zgodne: Δt₁ = ?

5. Po jakim czasie t₂ od startu wychylenia 1i 3 były zgodne lecz przeciwne do 2 i jak to długo Δt₂ trwało:

• t₂ = ?

• Δt₂ = ?

W D i E max 10% błędu.

Ich nazwy licząc od lewej to:

1. oscylator : ......

2. oscylator : ......

Kulki to symbol wielk. fiz. zw :

3. (wymienić jej nazwę)

i jeżeli jest ona 2 × większa to okres drgania układu(ów)

4. (wstaw nr układu(ów) A , B)

5. ....... się (wstaw liczbę) × .

x₁ i x₂ to wychylenia , których wartość

6. (może, musi) się zmieniać z czasem

7. i zawsze (może, musi) to być zależność: (wpisać ją)

Wybierz fałszywki odpowiedzi:

8. Gdy układy A i B są w rezonansie (T_A= = T_B) to k = = g i m = = l.

9. Z rysunku oscylatora A musi wynikać, że masa z prawej strony musi być największa.

10. Rys B: x₁=x₂ minimum 2×w okresie drgania.

11. A_A = = A_B w układach rezonansowych.

12. ω_A= = ω_B j. w.

13. Podczas ogrzewania sprężyny jej okres drgań wzrastał tzn. że stała sprężystości malała przy m = const.

14. W Kosmosie nie działał by ani układ A ani B.

15. Układ B mógłby zastąpić A gdyby cięgno było gumowe.

3. Wskaż błędy w rysunku.

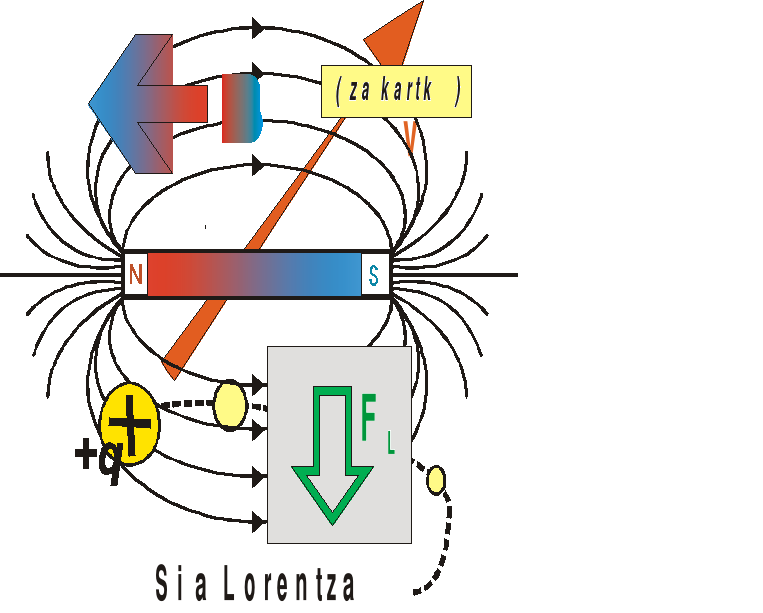
Rysunek do zadania wykonany w skali 1 : 5 . Obliczyć zmianę okresu wahadła po wykonaniu przez bloczek z którego nawija się wahadło 1,5 obrotu w zaznaczoną stronę. Wynik zapisać w postaci : T₁ : T₂ = k : l . Jak zmieni to v_max i a_max (opis werbalny lub formalny).

---