1. Wstęp teoretyczny

Zjawisko termoelektryczne polegające na powstawaniu różnicy potencjałów na styku dwóch różnych metali jest wykorzystywane do budowy termopar.

Termoparą (termoelementem lub termoogniwem) nazywamy obwód zbudowany z dwóch różnych metali lub półprzewodników, którego schemat przedstawiono na rysunku.

Rys. 1. Schemat termopary.

Jeżeli temperatury złącz różnią się od siebie to między punktami C i D powstaje siła termoelektryczna E. Siła ta jest wypadkową różnicy potencjałów Galvaniego oraz Thomsona. Dla niezbyt dużych różnic temperatur między złączami możemy założyć, że siła termoelektryczna jest proporcjonalna do różnicy temperatur T₁ - T₂.

Aby wyznaczyć siłę termoelektryczną E, do obwodu musimy dołączyć miernik.

Termopary najczęściej wykonane są z:

- miedzi i konstantanu

- platyny i platynorodu

- irydu i stopu irydu z rodem

2. Opis pomiaru i tabele

Schemat pomiarowy:

Spis przyrządów:

- Kuchenka elektryczna

- Termometr

- Naczynie do podgrzewania wody wraz z elektrycznym mieszadełkiem

- Termos

- Termopara

- Tygiel ze stopem Wooda

- Stoper

- Woltomierz cyfrowy V544

Oznaczenia:

U - napięcie odczytywane na miliwoltomierzu [mV];

U - błąd bezwzględny wartości napięcia równy wartości ±(1%U+2dgt) [mV];

t - temperatura odczytywana z termometru [^oC];

t - błąd bezwzględny odczytu wartości z termometru [^oC];

  czas odczytywany ze stopera podczas schładzania stopu metali [s];

  błąd bezwzględny odczytu czasu [s];

  współczynnik termoelektryczny termopary

  niepewność bezwzględna wyznaczenia współczynnika termoelektrycznego termopary
;

 niepewność względna wyznaczenia współczynnika termoelektrycznego termopary
;

S_x - odchylenie standardowe średniej

U_k - napięcie, przy którym występuje proces krzepnięcia [mV];

U_k - błąd bezwzględny wyznaczenia napięcia, przy którym występuje proces krzepnięcia [mV];

T_k - temperatura krzepnięcia stopu metali [deg];

T_k - błąd bezwzględny wyznaczenia temperatury krzepnięcia stopu metali [deg];

 błąd względny wyznaczenia temperatury krzepnięcia stopu metali [deg].

Tabela 1.

Pomiary wykonywano w zakresie temperatur 20^oC - 90,0^oC, mierząc napięcie wskazywane na miliwoltomierzu (począwszy od 20^oC co 2^oC).

Skalowanie termopary
t	∆t	U	∆U	α	∆α	∆α/α
[ºC]	[ºC]	[mV]	[mV]	[mV/deg]	[mV/deg]	[%]
20	1	0,636	0,008	0,04222	0,00022	0,53%
22			0,687				0,009
24			0,757				0,010
26			0,835				0,010
28			0,905				0,011
30			0,960				0,012
32			1,050				0,013
34			1,147				0,013
36			1,232				0,014
38			1,321				0,015
40			1,393				0,016
42			1,470				0,017
44			1,540				0,017
46			1,631				0,018
48			1,720				0,019
50			1,807				0,020
52			1,894				0,021
54			1,970				0,022
56			2,060				0,023
58			2,126				0,023
60			2,201				0,024
62			2,286				0,025
64			2,384				0,026
66			2,477				0,027
68			2,564				0,028
70			2,660				0,029
72			2,751				0,030
74			2,844				0,030
76			2,947				0,031
78			3,027				0,032
80			3,111				0,033
82			3,192				0,034
84			3,284				0,025
86			3,364				0,036
88			3,458				0,037
90			3,553				0,036

Za błąd pomiaru temperatury przyjąłem najmniejszą podziałkę termometru, czyli 1,0^oC.

Miliwoltomierz elektroniczny ustawiony na zakresie 10 mV charakteryzuje się błędem podstawowym
.

Obliczenia:

Współczynnik termoelektryczny  i jego błąd obliczyłem stosując regresję liniową, zgodnie z metodą najmniejszych kwadratów.

Dany wzór
przekształciłem do postaci
otrzymując
gdzie
,
. Dokładny wynik dla α i Δα otrzymałem używając arkusza ze strony LPF.

α	Δα	Δα/ α
[mV/deg]	[mV/deg]	[%]
0,04222	0,00022	0,53

Tabela 2.

Wykorzystano stop Wooda a pomiary wykonywano co 20 s od momentu zaprzestania podgrzewania (napięcie odczytane na miliwoltomierzu wynosiło 3,353 mV) aż do momentu gdy napięcie spadło poniżej 1,150 mV

	Wyznaczenie temperatury krzepnięcia stopu
Lp.		U	∆U	Uk	∆Uk	Tk	∆Tk	∆Tk/Tk
	[s]	[mV]	[mV]	[mV]	[mV]	[deg]	[deg]	[%]
1	0	3,353	0,036	2,493	0,051	59,0	1,5	2,5
2	20	2,971	0,030
3	40	2,701	0,030
4	60	2,573	0,030
5	80	2,544	0,027
6	100	2,540	0,027
7	120	2,535	0,027
8	140	2,527	0,027
9	160	2,523	0,027
10	180	2,514	0,027
11	200	2,504	0,027
12	220	2,496	0,027
13	240	2,489	0,027
14	260	2,478	0,027
15	280	2,465	0,027
16	300	2,442	0,026
17	320	2,410	0,026
18	340	2,363	0,026
19	360	2,295	0,025
20	380	2,213	0,024
21	400	2,135	0,023
22	420	2,066	0,023
23	440	2,005	0,022
24	460	1,949	0,021
25	480	1,897	0,021
26	500	1,897	0,020
27	520	1,805	0,020
28	540	1,765	0,020
29	560	1,721	0,020
30	580	1,668	0,020
31	600	1,633	0,018
32	620	1,610	0,018
33	640	1,581	0,018
34	660	1,563	0,018
35	680	1,538	0,017
36	700	1,517	0,017

Napięcie U_k obliczyłem jako średnią arytmetyczną wartości zaznaczonych kolorem czerwonym (wg. wykresu nr 2), a jego błąd obliczyłem stosując metodę Studenta-Fishera. Temperaturę krzepnięcia stopu wyznaczyłem ze wzoru:

, a jego niepewność obliczyłem stosując metodę różniczki zupełnej.

Obliczenia:

[mV]

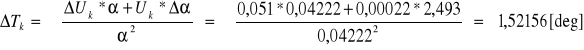
Wnioski

Przy cechowaniu termopary można zauważyć, że napięcie odczytywane na miliwoltomierzu cyfrowym rośnie wprost proporcjonalnie do wzrastającej temperatury. Współczynnikiem proporcjalności jest współczynnik termoelektryczny

 = 0,04222 ± 0,00022.

Skalowanie termopary służy do wycechowania danej termopary, którą można zastosować do rejestrowania temperatury w dowolnym przetworniku analogowo-cyfrowym. Termopara jest przetwornikiem T/U - temperatura/napięcie. Wyposażając miliwoltomierz w odpowiednią skalę można byłoby bezpośrednio mierzyć różnicę temperatur. Jednocześnie wyposażając miliwoltomierz w odpowiednie urządzenia można byłoby rejestrować zmiany temperatury, lub kontrolować procesy technologiczne zależne od temperatury.

Odczytaną z wykresu krzywej stygnięcia stopu wartością napięcia było

U_k=2,493 ±0,051 [mV]. Temperatura, w której jest obserwowane U_k jest równocześnie temperaturą przemiany fazowej.

Wykorzystany stop Wooda ma niską temperaturę krzepnięcia T_k=59,0± 1,5 [^oC]. Widać tu zasadność wyboru stopu Wooda ze względu na łatwość pomiaru i bezpieczeństwo.

---