![]()
, ![]()
ROZKŁAD NORMALNY - c.d.
![]()
, ![]()
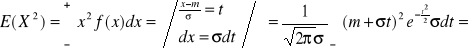
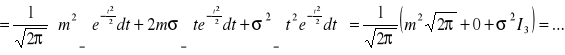
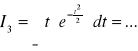
(przez części)![]()
![]()
.
![]()
, ![]()
, 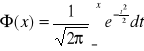
- dystrybuanta
Tw: ![]()
Dow: 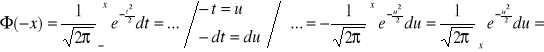
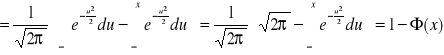
.
Np.: ![]()
Obliczyć ![]()
![]()
np2: ![]()
Obliczyć ![]()
![]()
![]()
Def: Zmienną losową Y nazywamy standaryzacją zmiennej losowej X; ![]()
.
Rozkład gamma:
Def: Funkcję 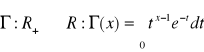
nazywamy funkcją gamma.
Własności:
![]()
![]()
; Jeżeli ![]()
![]()
dow: 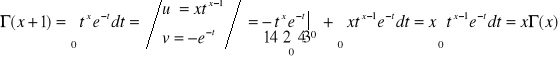
.
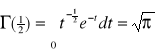
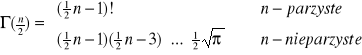
Def: Mówimy, że zmienna losowa X ma rozkład ![]()
-Eulera jeżeli jest zmienną losową o rozkładzie ciągłym i funkcji gęstości 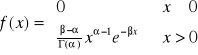
.
![]()
![]()
![]()
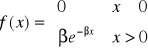
![]()
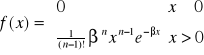
rozkład Erlanga
![]()
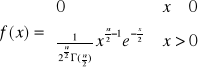
rozkład ![]()
o n stopniach swobody
Rozkład Beta:
Def: Funkcją beta nazywamy funkcje 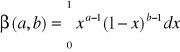
, ![]()
.
![]()
Def: Mówimy, że zmienna losowa ma rozkład beta, jeżeli jest zmienną losową o rozkładzie ciągłym i o funkcji gęstości 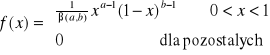
.
![]()
![]()
Rozkład t-Studenta:
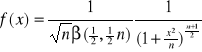
, ![]()
, n - liczba stopni swobody
![]()
, ![]()
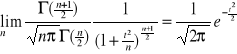
![]()
![]()
t-St.![]()
N(0,1)
FUNKCJE ZMIENNYCH LOSOWYCH
![]()
![]()
- zmienna losowa
![]()
- mierzalna (tzn. przeciwobraz zbioru borelowskiego jest zbiorem B.)
![]()
- też zmienna losowa
zał: ![]()
Mając rozkład zmiennej losowej X chcemy wyznaczyć rozkład zmiennej Y.
|
Lematy:
Tw: zał: ![]()
całkowalna na ![]()
teza: 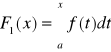
, 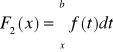
![]()
i ![]()
są ciągłe oraz
![]()
, ![]()
w każdym punkcie ciągłości funkcji ![]()
.
Tw: zał: ![]()
całkowalna w ![]()
, ![]()
różniczkowalna w ![]()
.
teza: 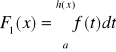
, 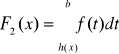
![]()
, ![]()
|
Tw: Jeżeli X jest zmienną losową o rozkładzie ciągłym i funkcji gęstości ![]()
, a ![]()
jest funkcja silnie monotoniczną, to gęstość ![]()
zmiennej losowej ![]()
wyrażą się wzorem ![]()
, gdzie ![]()
jest funkcją odwrotną do ![]()
.
Dow: 1) g silnie rosnąca ![]()
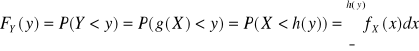
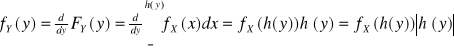
2) g silnie malejąca ![]()
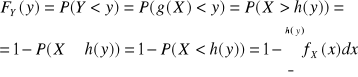
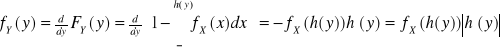
Tw: Jeżeli X ma rozkład normalny ![]()
, to ![]()
też ma rozkład normalny ![]()
![]()
.
Dow: ![]()
![]()
jest silnie monotoniczna
Spełnia założenia powyższego twierdzenia ![]()
![]()
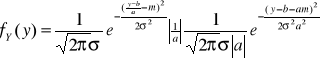
![]()
jest gęstością rozkładu
![]()
Wniosek: Jeżeli ![]()
, to ![]()
2
Luke Rachunek prawdopodobieństwa-wykład 23.4.2k+1